Mathematical Methods in the Physical Sciences
3rd Edition
ISBN: 9780471198260
Author: Mary L. Boas
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 13.5, Problem 13P
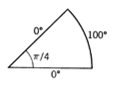
Find the steady-state distribution of temperature in the sector of a circular plate of radius 10 and angle
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The distribution system for the Herman Company consists of three plants, two warehouses, and four customers. Plant capacities and shipping costs per unit (in $) from each plant to each warehouse are as follows.
Warehouse
Plant
Capacity
1
2
1
4
7
450
2
8
5
600
3
5
6
380
Customer demand and shipping costs per unit (in $) from each warehouse to each customer are as follows.
Customer
Warehouse
1
2 3
1
6
4
8
2
3
6
7
7
Demand
300 300 300 400
(a) Develop a network representation of this problem. (Submit a file with a maximum size of 1 MB.)
Choose File No file chosen
This answer has not been graded yet.
(b) Formulate a linear programming model of the problem. (Let Plant 1 be node 1, Plant 2 be node 2, Plant 3 be node 3, Warehouse 1 be node 4, Warehouse 2 be node 5, Customer 1 be node 6, Customer 2 be node 7, Customer 3 be node 8, and Customer 4 be node 9. Express your answers in the form x;;, where x,; represents the number of units shipped from
node i to node j.)
Min 4x14+8x24+5x34+7x15 +5x25…
A linear programming computer package is needed.
Hanson Inn is a 96-room hotel located near the airport and convention center in Louisville, Kentucky. When a convention or a special event is in town, Hanson increases its normal room rates and takes reservations based on a revenue management system. A large profesional organization has scheduled its annual convention in Louisville for the first weekend in June. Hanson Inn agreed to make at least 50% of its
rooms available for convention attendees at a special convention rate in order to be listed as a recommended hotel for the convention. Although the majority of attendees at the annual meeting typically request a Friday and Saturday two-night package, some attendees may select a Friday night only or a Saturday night only reservation. Customers not attending the convention may also request a Friday and
Saturday two-night package, or make a Friday night only or Saturday night only reservation. Thus, six types of reservations are…
Questions
1. Identify and describe potential bias in the study.
2. Identify and describe the way in which the selected participants may or may not represent the population as a whole.
3. Identify and describe the possible problems with the end results since the majority will be from females rather than an even
split.
4. Identify and describe the possible problems with identifying females as possibly more vulnerable based on the data
collected.
5. Identify a possible null hypothesis and problems in how the study might address this null hypothesis.
6. Identify one possible method of improving the study design and describe how it would improve the validity of the
conclusions.
7. Identify a second possible method of improving the study design and describe how it would improve the validity of the
conclusions.
Chapter 13 Solutions
Mathematical Methods in the Physical Sciences
Ch. 13.1 - Assume from electrostatics the equations E=/0 and...Ch. 13.1 - Show that the expression u=sin(xvt) describing a...Ch. 13.1 - Assume from electrodynamics the following...Ch. 13.1 - Obtain the heat flow equation (1.3) as follows:...Ch. 13.2 - After you find the series solution of a problem,...Ch. 13.2 - T=0,0x10,100,10x20. Solve the semi-infinite plate...Ch. 13.2 - Solve the semi-infinite plate problem if the...Ch. 13.2 - Solve the semi-infinite plate problem if the...Ch. 13.2 - Show that the solutions of (2.5) can also be...Ch. 13.2 - Show that the series in (2.12) can be summed to...
Ch. 13.2 - Solve Problem 3 if the plate is cut off at height...Ch. 13.2 - Find the steady-state temperature distribution in...Ch. 13.2 - Solve Problem 2 if the plate is cut off at height...Ch. 13.2 - Find the steady-state temperature distribution in...Ch. 13.2 - Find the steady-state temperature distribution in...Ch. 13.2 - Find the temperature distribution in a rectangular...Ch. 13.2 - Find the steady-state temperature distribution in...Ch. 13.2 - In the rectangular plate problem, we have so far...Ch. 13.2 - Consider a finite plate, 10cm by 30cm, with two...Ch. 13.2 - Show that there is only one function u which...Ch. 13.3 - Verify the coefficients in equation (3.14).Ch. 13.3 - A bar 10 cm long with insulated sides is initially...Ch. 13.3 - In the initial steady state of an infinite slab of...Ch. 13.3 - At t=0, two flat slabs each 5cm thick, one at 0...Ch. 13.3 - Prob. 5PCh. 13.3 - Show that the following problem is easily solved...Ch. 13.3 - A bar of length l with insulated sides has its...Ch. 13.3 - A bar of length 2 is initially at 0. From t=0 on,...Ch. 13.3 - Solve Problem 8 if, for t0, the x=0 end of the bar...Ch. 13.3 - Separate the wave equation (1.4) into a space...Ch. 13.3 - Solve the particle in a box problem to find (x,t)...Ch. 13.3 - Do Problem 11 if (x,0)=sin2x on (0,1).Ch. 13.4 - Complete the plucked string problem to get...Ch. 13.4 - A string of length l has a zero initial velocity...Ch. 13.4 - Solve Problem 2 if the initial displacement is:Ch. 13.4 - Solve Problem 2 if the initial displacement is :Ch. 13.4 - A string of length l is initially stretched...Ch. 13.4 - Do Problem 5 if the initial velocity V(x)=(y/t)t=0...Ch. 13.4 - Solve Problem 5 if the initial velocity is:Ch. 13.4 - Solve Problem 5 if the initial velocity is...Ch. 13.4 - In each of the Problems 1 to 8,find the frequency...Ch. 13.4 - Verify that, if k=nT, then the sum of the two...Ch. 13.4 - Verify (4.16) and find a similar formula for a...Ch. 13.4 - In Sections 2, 3, 4, we have solved a number of...Ch. 13.4 - Do Problem 12 for f(x)=1cos2x on (0,).Ch. 13.4 - Do Problem 12 for f(x)=xx3 on (0, 1).Ch. 13.5 - Compute numerically the coefficients (5.16) of the...Ch. 13.5 - Find the steady-state temperature distribution in...Ch. 13.5 - Find the steady-state temperature distribution in...Ch. 13.5 - A flat circular plate of radius a is initially at...Ch. 13.5 - Do Problem 4 if the initial temperature...Ch. 13.5 - Consider Problem 4 if the initial temperature...Ch. 13.5 - Find the steady-state temperature distribution in...Ch. 13.5 - Water at 100 is flowing through a long pipe of...Ch. 13.5 - Find the steady-state distribution of temperature...Ch. 13.5 - A cube is originally at 100. From t=0 on, the...Ch. 13.5 - The following two R(r) equations arise in various...Ch. 13.5 - Separate Laplaces equation in two dimensions in...Ch. 13.5 - Find the steady-state distribution of temperature...Ch. 13.5 - Find the steady state temperature distribution in...Ch. 13.5 - Solve Problem 14 if the temperatures of the two...Ch. 13.6 - Continue Figure 6.1 to show the fundamental modes...Ch. 13.6 - Prob. 2PCh. 13.6 - Separate the wave equation in two-dimensional...Ch. 13.6 - Find the characteristic frequencies for sound...Ch. 13.6 - A square membrane of side l is distorted into the...Ch. 13.6 - Let V=0 in the Schrödinger equation (3.22) and...Ch. 13.6 - In your Problem 6 solutions, find some examples of...Ch. 13.6 - Do Problem 6 in polar coordinates to find the...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Find the steady-state temperature distribution...Ch. 13.7 - Do Problem 11 if the curved surface is held at...Ch. 13.7 - Find the electrostatic potential outside a...Ch. 13.7 - Find the steady-state temperature distribution in...Ch. 13.7 - A sphere initially at 0 has its surface kept at...Ch. 13.7 - Separate the wave equation in spherical...Ch. 13.7 - Do Problem 6.6 in 3 dimensional rectangular...Ch. 13.7 - Prob. 18PCh. 13.7 - Find the eigenfunctions and energy eigenvalues for...Ch. 13.7 - Write the Schrödinger equation (3.22) if is a...Ch. 13.7 - Prob. 21PCh. 13.7 - Find the energy eigenvalues and eigen functions...Ch. 13.8 - Show that the gravitational potential V=Gm/r...Ch. 13.8 - Using the formulas of Chapter 12, Section 5, sum...Ch. 13.8 - Do the problem in Example 1 for the case of a...Ch. 13.8 - Prob. 4PCh. 13.8 - Find the method of images for problem 4.Ch. 13.8 - Substitute (8.25) into (8.22) and use (8.23) and...Ch. 13.8 - Verify that the Green function in (8.29) is zero...Ch. 13.8 - Show that the Green function (8.28) which is zero...Ch. 13.8 - Show that our results can be extended to find the...Ch. 13.9 - Verify that (9.15) follows from (9.14). Hint: Use...Ch. 13.9 - A metal plate covering the first quadrant has the...Ch. 13.9 - Consider the heat flow problem of Section 3. Solve...Ch. 13.9 - A semi-infinite bar is initially at temperature...Ch. 13.9 - Prob. 5PCh. 13.9 - Continue the problem of Example 2 in the following...Ch. 13.9 - Continue with Problem 4 as in Problem 6.Ch. 13.10 - Find the steady-state temperature distribution in...Ch. 13.10 - Solve Problem 1 if T=0 for x=0,x=1,y=0, and T=1x...Ch. 13.10 - Solve Problem 1 if the sides x=0 and x=1 are...Ch. 13.10 - Find the steady-state temperature distribution in...Ch. 13.10 - A bar of length l is initially at 0. From t=0 on,...Ch. 13.10 - Do Problem 5 if the x=0 end is insulated and the...Ch. 13.10 - Solve Problem 2 if the sides x=0 and x=1 are...Ch. 13.10 - A slab of thickness 10cm has its two faces at 10...Ch. 13.10 - A string of length l has initial displacement...Ch. 13.10 - Solve Problem 5.7 if half the curved surface of...Ch. 13.10 - The series in Problem 5.12 can be summed (see...Ch. 13.10 - A plate in the shape of a quarter circle has...Ch. 13.10 - Sum the series in Problem 12 to get...Ch. 13.10 - A long cylinder has been cut into quarter...Ch. 13.10 - Repeat Problems 12 and 13 for a plate in the shape...Ch. 13.10 - Consider the normal modes of vibration for a...Ch. 13.10 - Sketch some of the normal modes of vibration for a...Ch. 13.10 - Repeat Problem 17 for a membrane in the shape of a...Ch. 13.10 - Prob. 19MPCh. 13.10 - Use Problem 7.16 to find the characteristic...Ch. 13.10 - The surface temperature of a sphere of radius 1 is...Ch. 13.10 - Find the interior temperature in a hemisphere if...Ch. 13.10 - Find the steady-state temperature in the region...Ch. 13.10 - Find the general solution for the steady-state...Ch. 13.10 - The Klein-Gordon equation is 2u=1/v22u/t2+2u. This...Ch. 13.10 - Prob. 26MPCh. 13.10 - Do Problem 26 for a rectangular membrane.Ch. 13.10 - Find the steady-state temperature in a...
Additional Math Textbook Solutions
Find more solutions based on key concepts
The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...
Basic Business Statistics, Student Value Edition
The following data were given in a study of a group of 1000 subscribers to a certain magazine: In reference to ...
A First Course in Probability (10th Edition)
1. If X is correlated with Y,
a. X causes Y.
b. increasing values of X go with increasing values of Y.
c. incr...
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Fill in each blanks so that the resulting statement is true. Any set of ordered pairs is called a/an _______. T...
College Algebra (7th Edition)
Write the bases, faces, edges and vertices of given figure.
Pre-Algebra Student Edition
If n is a counting number, bn, read______, indicates that there are n factors of b. The number b is called the_...
Algebra and Trigonometry (6th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 25.2. Find the Laurent series for the function 1/[z(z-1)] in the follow- ing domains: (a). 0<|z|< 1, (b). 1<|z, (c). 0arrow_forward25.5. Find the Laurent series for the function 1/[(z - 1)(-2)(z - 3)] in the following domains: (a). 0 3. شهریarrow_forward25.1. Expand each of the following functions f(z) in a Laurent series on the indicated domain: (a). z² - 2z+5 (2-2)(z² + 1)' (c). Log za 2 b (z - موجود 11, 29, where b>a> 1 are real, |z| > b.arrow_forward25.3. Find the Laurent series for the function z/[(22 + 1)(z² + 4)] in the following domains (a). 02.arrow_forward25.2. Find the Laurent series for the function 1/[z(z-1)] in the follow- ing domains: (a). 0<|z|< 1, (b). 1 <|z|, (c). 0<|z1|< 1, (d). 1< |z1|, (e). 1<|z2|<2.arrow_forward25.1. Expand each of the following functions f(z) in a Laurent series on the indicated domain: 22-2z+5 (z - 2) (z² + 1)' (z 11, 22 (a). (c). Log (2-8) where b>a> 1 are real, |z|> b. barrow_forward25.5. Find the Laurent series for the function 1/[(2-1)(z-2)(z-3)] in the following domains: (a). 0 3.arrow_forwardCan you explain how the error term in the CF Algorithm relates to the (m+1)th complete quotient? Also, what would be a good way to explain the connection between these two slides? How can one transition between them for a presentation?arrow_forwardHow can I explain the pi example in a presentation? I'm having trouble transitioning between these two slidesarrow_forwardMcGilla Golf has decided to sell a new line of golf clubs. The clubs will sell for $895 per set and have a variable cost of $431 per set. The company has spent $200,000 for a marketing study that determined the company will sell 80,000 sets per year for seven years. The marketing study also determined that the company will lose sales of 8,600 sets per year of its high-priced clubs. The high-priced clubs sell at $1,325 and have variable costs of $645. The company will also increase sales of its cheap clubs by 10,800 sets per year. The cheap clubs sell for $340 and have variable costs of $141 per set. The fixed costs each year will be $14,350,000. The company has also spent $1,500,000 on research and development for the new clubs. The plant and equipment required will cost $43,700,000 and will be depreciated on a straight-line basis. The new clubs will also require an increase in net working capital of $3,625,000 that will be returned at the end of the project. The tax rate is 25…arrow_forwardYou have been hired as an intern to run analyses on the data and report the results back to Sarah; the five questions that Sarah needs you to address are given below. Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship. Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. (In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size). Include the manufacturer dummy variable (Samsung=1, 0 otherwise) and estimate the relationship between screen size, price and manufacturer dummy as a multiple linear regression model. Interpret the…arrow_forwardDoes there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. How to take snapshots: if you use a MacBook, press Command+ Shift+4 to take snapshots. If you are using Windows, use the Snipping Tool to take snapshots. Question 1: Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship. Value of correlation coefficient: Direction of the relationship (positive, negative, or zero relationship): Strength of the relationship (strong/moderate/weak): Question 2: Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size. (The answer for the…arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Polar Coordinates Basic Introduction, Conversion to Rectangular, How to Plot Points, Negative R Valu; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=aSdaT62ndYE;License: Standard YouTube License, CC-BY