A Survey of Mathematics with Applications (10th Edition) - Standalone book
10th Edition
ISBN: 9780134112107
Author: Allen R. Angel, Christine D. Abbott, Dennis Runde
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 13.3, Problem 16E
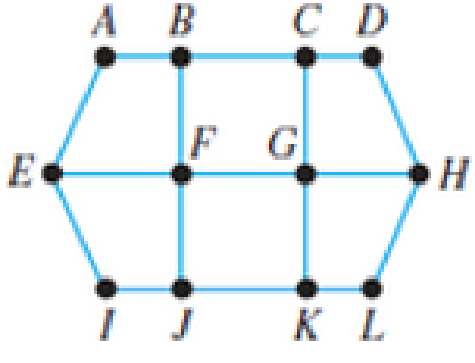
In Exercises 15-18, determine two different Hamilton circuits in each of the following graphs.
16. 
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
3 Show that it is not possible to creak
a graph with 9 vertices such that
the degree
(
a
of
every
vertex is 3.
Total number of hamiltonian circuits of the complete graph K.
К is
5
36 circuits
24 circuits
12 circuits
48 circuits
Previo
Construct a connected simple graph, that has no circuit, with vertices M, N, 0, P, Q, R, S, T, U such that the degree of O is 4.
Chapter 13 Solutions
A Survey of Mathematics with Applications (10th Edition) - Standalone book
Ch. 13.1 - In Exercises 1-8, fill in the blanks with an...Ch. 13.1 - In Exercises 1-8, fill in the blanks with an...Ch. 13.1 - In Exercises 1-8, fill in the blanks with an...Ch. 13.1 - In Exercises 1-8, fill in the blanks with an...Ch. 13.1 - Prob. 5ECh. 13.1 - In Exercises 1-8, fill in the blanks with an...Ch. 13.1 - Prob. 7ECh. 13.1 - Prob. 8ECh. 13.1 - In Exercises 9-14, create a graph with the given...Ch. 13.1 - In Exercises 9-14, create a graph with the given...
Ch. 13.1 - In Exercises 9-14, create a graph with the given...Ch. 13.1 - In Exercises 9-14, create a graph with the given...Ch. 13.1 - In Exercises 9-14, create a graph with the given...Ch. 13.1 - Prob. 14ECh. 13.1 - In Exercises 15-20, use the graph below to answer...Ch. 13.1 - In Exercises 15-20, use the graph below to answer...Ch. 13.1 - In Exercises 15-20, use the graph below to answer...Ch. 13.1 - In Exercises 15-20, use the graph below to answer...Ch. 13.1 - In Exercises 15-20, use the graph below to answer...Ch. 13.1 - Prob. 20ECh. 13.1 - Modified Knigsberg Bridge Problems In Exercises 21...Ch. 13.1 - Prob. 22ECh. 13.1 - Other Navy Regions In Exercises 23 and 24, the...Ch. 13.1 - Prob. 24ECh. 13.1 - Central America The map below shows the countries...Ch. 13.1 - Northern Africa The map below shows the countries...Ch. 13.1 - For Exercises 27-30, use a graph to represent the...Ch. 13.1 - Prob. 28ECh. 13.1 - Prob. 29ECh. 13.1 - For Exercises 27-30, use a graph to represent the...Ch. 13.1 - Representing a Neighborhood The map of the Tree...Ch. 13.1 - Prob. 32ECh. 13.1 - In Exercises 33-36, determine whether the graph...Ch. 13.1 - Prob. 34ECh. 13.1 - Prob. 35ECh. 13.1 - Prob. 36ECh. 13.1 - In Exercises 37-40, a connected graph is shown....Ch. 13.1 - Prob. 38ECh. 13.1 - In Exercises 37-40, a connected graph is shown....Ch. 13.1 - Prob. 40ECh. 13.1 - Poll your entire class to determine which students...Ch. 13.1 - Attempt to draw a graph that has an odd number of...Ch. 13.1 - Draw four different graphs and then for each...Ch. 13.1 - Facebook Friends Read the Recreational Mathematics...Ch. 13.1 - Use a graph to represent a. the floor plan of your...Ch. 13.2 - In Exercises 1-6, fill in the blanks with an...Ch. 13.2 - In Exercises 1-6, fill in the blanks with an...Ch. 13.2 - In Exercises 1-6, fill in the blanks with an...Ch. 13.2 - In Exercises 1-6, fill in the blanks with an...Ch. 13.2 - In Exercises 1-6, fill in the blanks with an...Ch. 13.2 - In Exercises 1-6, fill in the blanks with an...Ch. 13.2 - For Exercises 7-10, use the following graph. 7....Ch. 13.2 - Prob. 8ECh. 13.2 - For Exercises 7-10, use the following graph. 9 Is...Ch. 13.2 - Prob. 10ECh. 13.2 - For Exercises 11-14, use the following graph. 11....Ch. 13.2 - Prob. 12ECh. 13.2 - For Exercises 11-14, use the following graph. 13....Ch. 13.2 - Prob. 14ECh. 13.2 - For Exercises 15-20, use the following graph. 15....Ch. 13.2 - Prob. 16ECh. 13.2 - For Exercises 15-20, use the following graph. 17...Ch. 13.2 - Prob. 18ECh. 13.2 - For Exercises 15-20, use the following graph. 19...Ch. 13.2 - For Exercises 15-20, use the following graph. 20...Ch. 13.2 - Prob. 21ECh. 13.2 - Revisiting the Knigsberg Bridge Problem In...Ch. 13.2 - Prob. 23ECh. 13.2 - Other Navy Regions In Exercises 23 and 24, the...Ch. 13.2 - Areas of the World In Exercises 25-28 use each map...Ch. 13.2 - Prob. 26ECh. 13.2 - Prob. 27ECh. 13.2 - Prob. 28ECh. 13.2 - Locking Doors Recall Joe from Example 5 on page...Ch. 13.2 - Prob. 30ECh. 13.2 - Prob. 31ECh. 13.2 - Locking Doors Recall Joe from Example 5 on page...Ch. 13.2 - Prob. 33ECh. 13.2 - Prob. 34ECh. 13.2 - In Exercises 35-38, use Fleurys algorithm to...Ch. 13.2 - Prob. 36ECh. 13.2 - Prob. 37ECh. 13.2 - Prob. 38ECh. 13.2 - In Exercises 39-44, use Fleurys algorithm to...Ch. 13.2 - Prob. 40ECh. 13.2 - In Exercises 39-44, use Fleurys algorithm to...Ch. 13.2 - Prob. 42ECh. 13.2 - Prob. 43ECh. 13.2 - Prob. 44ECh. 13.2 - Prob. 45ECh. 13.2 - Prob. 46ECh. 13.2 - Determine an Euler circuit for the Country Oaks...Ch. 13.2 - Prob. 48ECh. 13.2 - Prob. 49ECh. 13.2 - Prob. 50ECh. 13.2 - Imagine a very large connected graph that has 400...Ch. 13.2 - Prob. 52ECh. 13.2 - Imagine a very large connected graph that has 400...Ch. 13.2 - Prob. 54ECh. 13.2 - Prob. 56ECh. 13.2 - Prob. 57ECh. 13.3 - In Exercises 1-8, fill in the blanks with an...Ch. 13.3 - In Exercises 1-8, fill in the blanks with an...Ch. 13.3 - In Exercises 1-8, fill in the blanks with an...Ch. 13.3 - In Exercises 1-8, fill in the blanks with an...Ch. 13.3 - In Exercises 1-8, fill in the blanks with an...Ch. 13.3 - In Exercises 1-8, fill in the blanks with an...Ch. 13.3 - In Exercises 1-8, fill in the blanks with an...Ch. 13.3 - In Exercises 1-8, fill in the blanks with an...Ch. 13.3 - In Exercises 9-14, determine two different...Ch. 13.3 - In Exercises 9-14, determine two different...Ch. 13.3 - In Exercises 9-14, determine two different...Ch. 13.3 - In Exercises 9-14, determine two different...Ch. 13.3 - In Exercises 9-14, determine two different...Ch. 13.3 - Prob. 14ECh. 13.3 - In Exercises 15-18, determine two different...Ch. 13.3 - In Exercises 15-18, determine two different...Ch. 13.3 - In Exercises 15-18, determine two different...Ch. 13.3 - Prob. 18ECh. 13.3 - Draw a complete graph with four vertices.Ch. 13.3 - Prob. 20ECh. 13.3 - College Visits Nick is a high school student who...Ch. 13.3 - Prob. 22ECh. 13.3 - Inspecting Weigh Stations Sally lives in...Ch. 13.3 - Prob. 24ECh. 13.3 - Running Errands on Campus Mary needs to run...Ch. 13.3 - Prob. 26ECh. 13.3 - A Family Vacation The Ackermans live in...Ch. 13.3 - Prob. 28ECh. 13.3 - Package Delivery Laurice works for FedEx and is in...Ch. 13.3 - Basketball Teams Jasmine lives in Elko, Nevada...Ch. 13.3 - Prob. 31ECh. 13.3 - Cranberry Plants Altay lives in Boston,...Ch. 13.3 - Prob. 33ECh. 13.3 - Prob. 34ECh. 13.3 - Prob. 35ECh. 13.4 - In Exercises 1-6, fill in the blanks with an...Ch. 13.4 - Prob. 2ECh. 13.4 - Prob. 3ECh. 13.4 - Prob. 4ECh. 13.4 - Prob. 5ECh. 13.4 - Prob. 6ECh. 13.4 - A Family Tree Use a tree to show the parent-child...Ch. 13.4 - Prob. 8ECh. 13.4 - Corporate Structure Use a tree to show the...Ch. 13.4 - Prob. 10ECh. 13.4 - Prob. 11ECh. 13.4 - Prob. 12ECh. 13.4 - Prob. 13ECh. 13.4 - Prob. 14ECh. 13.4 - Prob. 15ECh. 13.4 - Prob. 16ECh. 13.4 - Prob. 17ECh. 13.4 - Prob. 18ECh. 13.4 - Prob. 19ECh. 13.4 - Prob. 20ECh. 13.4 - Prob. 21ECh. 13.4 - Prob. 22ECh. 13.4 - Prob. 23ECh. 13.4 - Prob. 24ECh. 13.4 - Prob. 25ECh. 13.4 - Prob. 26ECh. 13.4 - Prob. 27ECh. 13.4 - Prob. 28ECh. 13.4 - Prob. 29ECh. 13.4 - Prob. 30ECh. 13.4 - Prob. 31ECh. 13.4 - Prob. 32ECh. 13.4 - Prob. 33ECh. 13.4 - College Structure Create a tree that shows the...Ch. 13.4 - Prob. 35ECh. 13 - In Exercises 1 and 2, create a graph with the...Ch. 13 - Prob. 2RECh. 13 - In Exercises 3 and 4, use the following graph 3....Ch. 13 - Prob. 4RECh. 13 - Prob. 5RECh. 13 - School Floor Plan The drawing below shows the...Ch. 13 - Prob. 7RECh. 13 - Prob. 8RECh. 13 - Prob. 9RECh. 13 - Prob. 10RECh. 13 - Prob. 11RECh. 13 - Prob. 12RECh. 13 - Prob. 13RECh. 13 - Prob. 14RECh. 13 - a. The drawing below shows the floor plan of a...Ch. 13 - Prob. 16RECh. 13 - Prob. 17RECh. 13 - Use Fleury's algorithm to determine an Euler...Ch. 13 - Prob. 19RECh. 13 - Prob. 20RECh. 13 - Prob. 21RECh. 13 - Prob. 22RECh. 13 - Prob. 23RECh. 13 - Visiting Sales Offices Jennifer is the sales...Ch. 13 - Prob. 25RECh. 13 - Prob. 26RECh. 13 - Prob. 27RECh. 13 - Prob. 28RECh. 13 - Prob. 1TCh. 13 - Prob. 2TCh. 13 - Prob. 3TCh. 13 - Prob. 4TCh. 13 - Prob. 5TCh. 13 - Prob. 6TCh. 13 - Prob. 7TCh. 13 - Use Fleurys algorithm to determine an Euler...Ch. 13 - Prob. 9TCh. 13 - Prob. 10TCh. 13 - Prob. 11TCh. 13 - Prob. 12TCh. 13 - Prob. 13TCh. 13 - Prob. 14TCh. 13 - Prob. 15TCh. 13 - Prob. 16TCh. 13 - Prob. 17TCh. 13 - Prob. 18TCh. 13 - Prob. 19TCh. 13 - Prob. 20T
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Give an example of two non-isomorphic graphs each containing 5 vertices and 8 edges. Give complete justification.arrow_forwardHow can one prove a graph is connected?arrow_forwardWhat is the minimum number of colors you need to color the vertices of this graph such that if two vertices are adjacent they receive different colors?arrow_forward
- (B) |Consider the graphs K,, K,3 and K,3 in figure given below. Find and draw an Euler |(traversable) path or an Euler circuit of each graph, if it exists. If it does not, why not? 會圣文 D (a) (b) (c) Answer:arrow_forwardLet G be a simple graph with exactly 11 vertices. Prove that G or its complement G must benon-planar. Hint: The maximum number of edges in a planar graph with n vertices is 3n − 6.Please write in complete sentences, include all details, showall of your work, and clarify all of your reasoning.arrow_forward6.) Determine the fewest number of different colors needed to color this graph so that every node is colored differently from its neighbors.arrow_forward
- Caroline has to check the stop signs at every intersection in his hometown. She parks her car in the parking lot of the transportation department and needs to end up back at her car. She only wants to check each intersection one time. Which graph would be best for this scenario? " O Hamiltonian cvcle O Euler path Hamiltonian path O Euler tourarrow_forwardChess is a board game, where the board is made up of 64 squares arranged in an 8-by-8 grid. One of the pieces is a rook, which can move from its current square any number of spaces either vertically or horizontally (but not diagonally) in a single turn. Discuss how you could use graphs to show that a rook can get from its current square to any other square on the board in at most two turns. You’re encouraged to utilize relevant graph definitions, problems, and algorithms where appropriate.arrow_forwardWe say that two graphs are distinct if and only if these two graphs are not isomorphic. How many distinct connected simple circuit-free graphs with 6 vertices are there?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY