
Two gorgeous polyhedra can be created by stellating an icosahedron and a dodecahedron. SteI/ating means making starlike. Imagine turning each face of an icosahedron into a “star point"-namely, a pyramid whose base is a triangular face of th icosahedron. Likewise, imagine turning each face of a dodecahedron into a star point-namely, a pyramid whose base is a pentagonal face of the dodecahedron. A stellated icosahedron will then have 20 star points, whereas a stellated dodecahedron will have 12 star points.
a. Make 20 copies of Figure 13.15 on card stock. Cut, fold, and tape them to make 20 triangle-based pyramid star points. (The pattern makes star-point pyramids that don’t have bases.) Tape the star points together as though you were making an icosahedron out of their (open) bases.
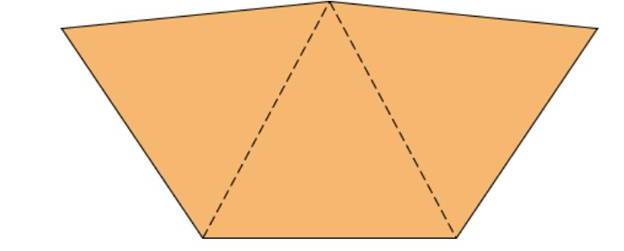
Figure 13.15 Pattern for a star point of an icosahedron.
b. Make 12 copies of Figure 13.16 on card stock. Cut, fold, and tape them to make 12 pentagon-based pyramid star points. (The pattern makes star point pyramids that don’t have bases.) Tape the star points together as though you were making a dodecahedron out of their (open) bases.

Figure 13.16 pattern for a star point of a dodecahedron
Want to see the full answer?
Check out a sample textbook solution
Chapter 13 Solutions
Mathematics for Elementary Teachers with Activities (5th Edition)
Additional Math Textbook Solutions
Basic College Mathematics
Differential Equations: An Introduction to Modern Methods and Applications
Introductory Mathematics for Engineering Applications
Mathematics All Around (6th Edition)
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Pathways to Math Literacy (Loose Leaf)
- For a regular hexahedron, find the number of faces, vertices, and edges in the polyhedron. Then verify Eulers equation for that polyhedron.arrow_forwardFor a regular tetrahedron, find the number of faces, vertices, and edges in the polyhedron. Then verify Eulers equation for that polyhedron.arrow_forwardIn the illustration, point M is the midpoint of the hypotenuse of right triangle AOB. Show that the area of rectangle OLMN is one-half of the area of triangle AOB.arrow_forward
- Find the lengths of the side and the radius of a regular hexagon whose apothem has the length 10 m.arrow_forwardFind the lengths of the apothem and the radius of a regular hexagon whose sides have length 6 cm.arrow_forwardWhich of these two polyhedrons is concave? Note that the interior dihedral angle formed by the planes containing EJF and KJF is larger than 180 .arrow_forward
- Find the lengths of the apothem and the radius of a square whose sides have length 10 in.arrow_forwarda Are any two regular pentagons similar? b Are any two equiangular pentagons similar?arrow_forwardDraw an obtuse triangle and construct the three perpendicular bisectors of its sides. Do the perpendicular bisectors of the three sides appear to meet at a common point?arrow_forward
- What is the general name of the point of concurrence for the three altitudes of a triangle?arrow_forwardA trapezoid is a four-sided figure that contains one pair of parallel sides. Which sides of the trapezoid MNPQ appear to be parallel?arrow_forwardWhat type quadrilateral is formed when the midpoints of the sides of an isosceles trapezoid are joined in order.arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL





