
Concept explainers
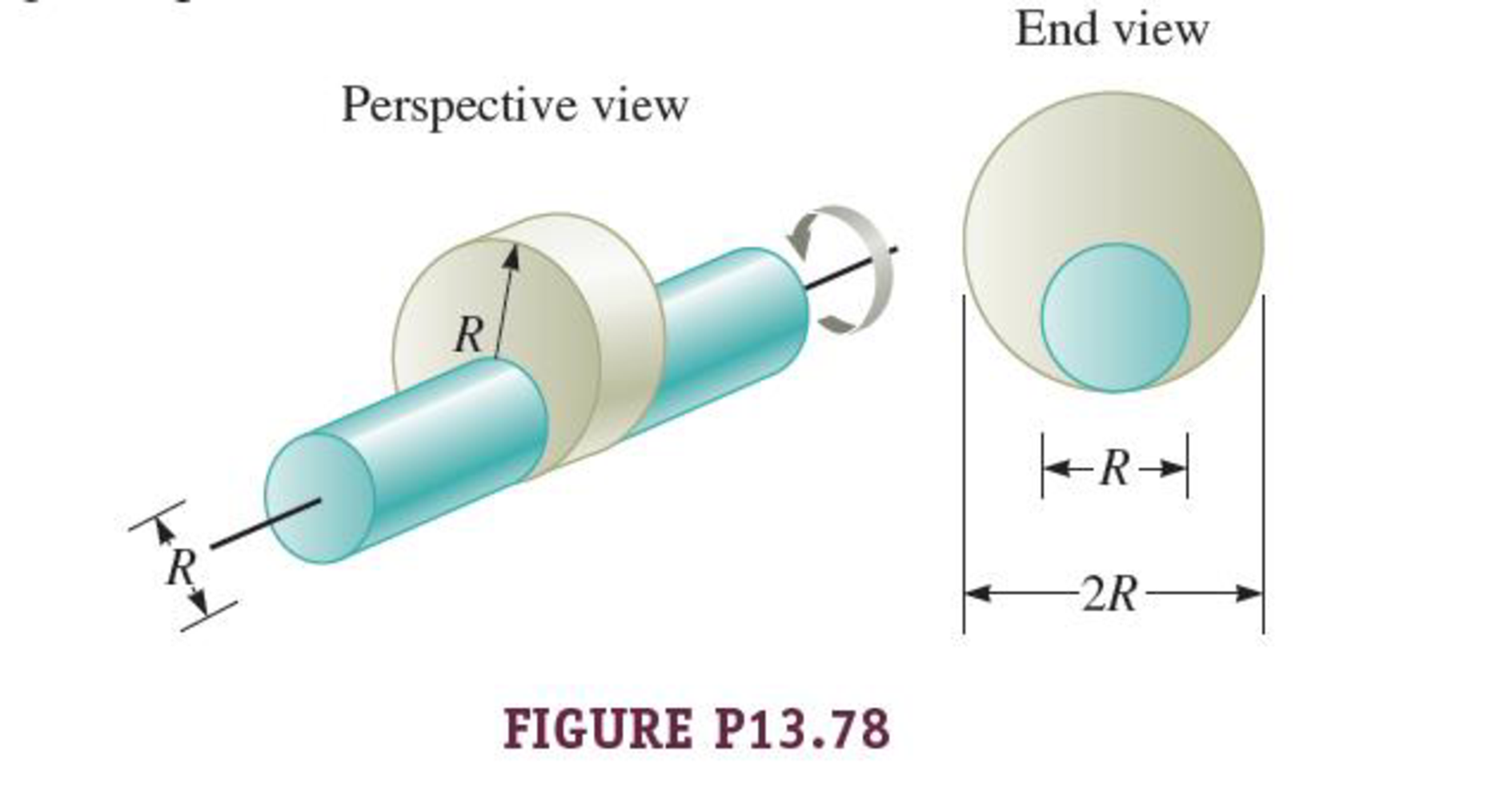
A cam of mass M is in the shape of a circular disk of diameter 2R with an off-center circular hole of diameter R is mounted on a uniform cylindrical shaft whose diameter matches that of the hole (Fig. P1 3.78). a. What is the rotational inertia of the cam and shaft around the axis of the shaft? b. What is the rotational kinetic energy of the cam and shaft if the system rotates with angular speed ω around this axis?
(a)
The rotational inertia of the cam and shaft around the axis of the shaft.
Answer to Problem 78PQ
The rotational inertia of the cam and shaft around the axis of the shaft is 2324McamR2+12Mshaft(R2)2 .
Explanation of Solution
Write the equation for the rotational inertia of the cam and shaft around the axis of the shaft.
Icam-shaft=Icam+Ishaft (I)
Here, Icam-shaft is the rotational inertia of the cam and shaft around the axis of the shaft, Icam is the rotational inertia of the cam and Ishaft is the rotational inertia of the shaft.
Rotational inertia of the cam is the difference of the rotational inertia of the solid disk about an axis R/2 from the center of mass and the rotational inertia of the small disk of radius R/2 with a rotation axis through its center.
Write the equation for the rotational inertia of the cam.
Icam=Idisk−Ismall disk (II)
Here, Idisk is the rotational inertia of the solid disk about an axis R/2 from the center of mass and Ismall disk is the rotational inertia of the small disk of radius R/2 with a rotation axis through its center.
The rotational inertia of the solid disk bout an axis R/2 from its center of mass can be found using the parallel axis theorem.
Write the equation for Idisk .
Idisk=ICM+Mdisk(R2)2 (III)
Here, ICM is the rotational inertia of the disk about its center of mass and R is the radius of the cam and Mdisk is the mass of the disk.
Write the equation for the rotational inertia of the disk about its center of mass.
ICM=12MdiskR2
Put the above equation in equation (III).
Idisk=12MdiskR2+14MdiskR2=34MdiskR2 (IV)
With half the radius, the cut away small disk has one-quarter the face area, one-quarter the volume and one-quarter the mass of the original solid disk.
Write the expression for the ratio of the mass of the small disk to the mass of the original solid disk.
Msmall diskMdisk=(R/2)2R2=R24R2=14
Here, Msmall disk is the mass of the small disk.
Rewrite the above equation for Msmall disk .
Msmall disk=14Mdisk (V)
Write the equation for the rotational inertia of the small disk about an axis through its center of mass.
Ismall disk=12Msmall disk(R2)2=18Msmall diskR2
Here, Ismall disk is the rotational inertia of the small disk about an axis through its center of mass and (R/2) is the radius of the small disk.
Put equation (V) in the above equation.
Ismall disk==18(14Mdisk)R2=132MdiskR2 (VI)
Put equations (IV) and (VI) in equation (II).
Icam=34MdiskR2−132MdiskR2=MdiskR2(34−132)=MdiskR2(2432−132)=2332MdiskR2 (VII)
Write the equation for the mass of the cam.
Mcam=Mdisk−Msmall disk
Here, Mcam is the mass of the cam.
Put equation (V) in the above equation.
Mcam=Mdisk−14Mdisk=34Mdisk (VIII)
Multiply and divide the right hand side of equation (VII) with Mcam .
Icam=2332MdiskR2McamMcam
Put equation (VIII) in the denominator of the above equation.
Icam=2332MdiskR2Mcam34Mdisk=McamR2(2332)(43)=2324McamR2 (IX)
Write the equation for the rotational inertia of the shaft.
Ishaft=12Mshaft(R2)2 (X)
Here, Mshaft is the mass of the shaft.
Conclusion:
Put equations (IX) and (X) in equation in equation (I).
Icam-shaft=2324McamR2+12Mshaft(R2)2
Therefore, the rotational inertia of the cam and shaft around the axis of the shaft is 2324McamR2+12Mshaft(R2)2 .
(b)
The rotational kinetic energy of the cam and shaft if the system rotates with angular speed ω around the axis.
Answer to Problem 78PQ
The rotational kinetic energy of the cam and shaft if the system rotates with angular speed ω around the axis is 2348McamR2ω2+116MshaftR2ω2 .
Explanation of Solution
Write the equation for the rotational kinetic energy of the cam and the shaft.
Ktotal=Kcam+Kshaft (XI)
Here, Ktotal is the rotational kinetic energy of the system of cam and the shaft, Kcam is the rotational kinetic energy of the cam and Kshaft is the rotational kinetic energy of the shaft.
Write the equation for Kcam .
Kcam=12Icamω2
Put equation (IX) in the above equation.
Kcam=12(2324McamR2)ω2=2348McamR2ω2 (XII)
Write the equation for Kshaft .
Kshaft=12Ishaftω2
Put equation (X) in the above equation.
Kshaft=12(12Mshaft(R2)2)ω2=116MshaftR2ω2 (XIII)
Conclusion:
Put equations (XII) and (XIII) in equation (XI).
Ktotal=2348McamR2ω2+116MshaftR2ω2
Therefore, the rotational kinetic energy of the cam and shaft if the system rotates with angular speed ω around the axis is 2348McamR2ω2+116MshaftR2ω2 .
Want to see more full solutions like this?
Chapter 13 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- Figure 29-43 Problem 12. ••13 In Fig. 29-44, point P₁ is at distance R = 13.1 cm on the perpendicular bisector of a straight wire of length L = 18.0 cm carrying current i = 58.2 mA. (Note that the wire is not long.) What is the magnitude of the magnetic field at P₁ due to i? P2° R R Larrow_forwardCheckpoint 1 The figure shows the current i in a single-loop circuit with a battery B and a resistance R (and wires of neg- ligible resistance). (a) Should the emf arrow at B be drawn pointing leftward or rightward? At points a, B C R b, and c, rank (b) the magnitude of the current, (c) the electric potential, and (d) the electric potential energy of the charge carriers, greatest first.arrow_forwardPls help ASAParrow_forward
- Pls help asaparrow_forwardPls help asaparrow_forward3. If the force of gravity stopped acting on the planets in our solar system, what would happen? a) They would spiral slowly towards the sun. b) They would continue in straight lines tangent to their orbits. c) They would continue to orbit the sun. d) They would fly straight away from the sun. e) They would spiral slowly away from the sun. 4. 1 The free-body diagram of a wagon being pulled along a horizontal surface is best represented by A F N B C 0 Ꭰ FN E a) A b) B c) C app app The app 10 app d) e) ס ח D E 10 apparrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





