Physics for Scientists and Engineers: Foundations and Connections
1st Edition
ISBN: 9781133939146
Author: Katz, Debora M.
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 13, Problem 74PQ
When a person jumps off a diving platform, she imparts some amount of
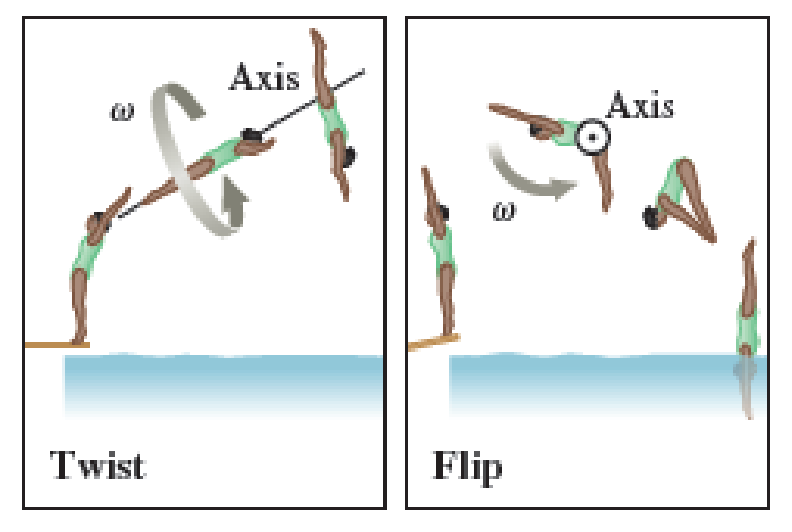
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
air is pushed steadily though a forced air pipe at a steady speed of 4.0 m/s. the pipe measures 56 cm by 22 cm. how fast will air move though a narrower portion of the pipe that is also rectangular and measures 32 cm by 22 cm
No chatgpt pls will upvote
13.87 ... Interplanetary Navigation. The most efficient way
to send a spacecraft from the earth to another planet is by using a
Hohmann transfer orbit (Fig. P13.87). If the orbits of the departure
and destination planets are circular, the Hohmann transfer orbit is an
elliptical orbit whose perihelion and aphelion are tangent to the
orbits of the two planets. The rockets are fired briefly at the depar-
ture planet to put the spacecraft into the transfer orbit; the spacecraft
then coasts until it reaches the destination planet. The rockets are
then fired again to put the spacecraft into the same orbit about the
sun as the destination planet. (a) For a flight from earth to Mars, in
what direction must the rockets be fired at the earth and at Mars: in
the direction of motion, or opposite the direction of motion? What
about for a flight from Mars to the earth? (b) How long does a one-
way trip from the the earth to Mars take, between the firings of the
rockets? (c) To reach Mars from the…
Chapter 13 Solutions
Physics for Scientists and Engineers: Foundations and Connections
Ch. 13.1 - CASE STUDY When Is Energy Conserved? Under what...Ch. 13.6 - Figure 13.24 shows a particle with momentum p....Ch. 13.7 - Prob. 13.3CECh. 13.7 - Prob. 13.4CECh. 13.7 - Prob. 13.5CECh. 13 - Prob. 1PQCh. 13 - Prob. 2PQCh. 13 - A Frisbee flies across a field. Determine if the...Ch. 13 - Prob. 4PQCh. 13 - Prob. 5PQ
Ch. 13 - Rotational Inertia Problems 5 and 6 are paired. 5....Ch. 13 - A 12.0-kg solid sphere of radius 1.50 m is being...Ch. 13 - A figure skater clasps her hands above her head as...Ch. 13 - A solid sphere of mass M and radius Ris rotating...Ch. 13 - Suppose a disk having massMtot and radius R is...Ch. 13 - Problems 11 and 12 are paired. A thin disk of...Ch. 13 - Given the disk and density in Problem 11, derive...Ch. 13 - A large stone disk is viewed from above and is...Ch. 13 - Prob. 14PQCh. 13 - A uniform disk of mass M = 3.00 kg and radius r =...Ch. 13 - Prob. 16PQCh. 13 - Prob. 17PQCh. 13 - The system shown in Figure P13.18 consisting of...Ch. 13 - A 10.0-kg disk of radius 2.0 m rotates from rest...Ch. 13 - Prob. 20PQCh. 13 - Prob. 21PQCh. 13 - In Problem 21, what fraction of the kinetic energy...Ch. 13 - Prob. 23PQCh. 13 - Prob. 24PQCh. 13 - Prob. 25PQCh. 13 - A student amuses herself byspinning her pen around...Ch. 13 - The motion of spinning a hula hoop around one's...Ch. 13 - Prob. 28PQCh. 13 - Prob. 29PQCh. 13 - Prob. 30PQCh. 13 - Sophia is playing with a set of wooden toys,...Ch. 13 - Prob. 32PQCh. 13 - A spring with spring constant 25 N/m is compressed...Ch. 13 - Prob. 34PQCh. 13 - Prob. 35PQCh. 13 - Prob. 36PQCh. 13 - Prob. 37PQCh. 13 - Prob. 38PQCh. 13 - A parent exerts a torque on a merry-go-round at a...Ch. 13 - Prob. 40PQCh. 13 - Today, waterwheels are not often used to grind...Ch. 13 - Prob. 42PQCh. 13 - A buzzard (m = 9.29 kg) is flying in circular...Ch. 13 - An object of mass M isthrown with a velocity v0 at...Ch. 13 - A thin rod of length 2.65 m and mass 13.7 kg is...Ch. 13 - A thin rod of length 2.65 m and mass 13.7 kg is...Ch. 13 - Prob. 47PQCh. 13 - Two particles of mass m1 = 2.00 kgand m2 = 5.00 kg...Ch. 13 - A turntable (disk) of radius r = 26.0 cm and...Ch. 13 - CHECK and THINK Our results give us a way to think...Ch. 13 - Prob. 51PQCh. 13 - Prob. 52PQCh. 13 - Two children (m = 30.0 kg each) stand opposite...Ch. 13 - A disk of mass m1 is rotating freely with constant...Ch. 13 - Prob. 55PQCh. 13 - Prob. 56PQCh. 13 - The angular momentum of a sphere is given by...Ch. 13 - Prob. 58PQCh. 13 - Prob. 59PQCh. 13 - Prob. 60PQCh. 13 - Prob. 61PQCh. 13 - Prob. 62PQCh. 13 - A uniform cylinder of radius r = 10.0 cm and mass...Ch. 13 - Prob. 64PQCh. 13 - A thin, spherical shell of mass m and radius R...Ch. 13 - To give a pet hamster exercise, some people put...Ch. 13 - Prob. 67PQCh. 13 - Prob. 68PQCh. 13 - The velocity of a particle of mass m = 2.00 kg is...Ch. 13 - A ball of mass M = 5.00 kg and radius r = 5.00 cm...Ch. 13 - A long, thin rod of mass m = 5.00 kg and length =...Ch. 13 - A solid sphere and a hollow cylinder of the same...Ch. 13 - A uniform disk of mass m = 10.0 kg and radius r =...Ch. 13 - When a person jumps off a diving platform, she...Ch. 13 - One end of a massless rigid rod of length is...Ch. 13 - A uniform solid sphere of mass m and radius r is...Ch. 13 - Prob. 77PQCh. 13 - A cam of mass M is in the shape of a circular disk...Ch. 13 - Prob. 79PQCh. 13 - Consider the downhill race in Example 13.9 (page...Ch. 13 - Prob. 81PQ
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- No chatgpt pls will upvotearrow_forwarda cubic foot of argon at 20 degrees celsius is isentropically compressed from 1 atm to 425 KPa. What is the new temperature and density?arrow_forwardCalculate the variance of the calculated accelerations. The free fall height was 1753 mm. The measured release and catch times were: 222.22 800.00 61.11 641.67 0.00 588.89 11.11 588.89 8.33 588.89 11.11 588.89 5.56 586.11 2.78 583.33 Give in the answer window the calculated repeated experiment variance in m/s2.arrow_forward
- How can i solve this if n1 (refractive index of gas) and n2 (refractive index of plastic) is not known. And the brewsters angle isn't knownarrow_forward2. Consider the situation described in problem 1 where light emerges horizontally from ground level. Take k = 0.0020 m' and no = 1.0001 and find at which horizontal distance, x, the ray reaches a height of y = 1.5 m.arrow_forward2-3. Consider the situation of the reflection of a pulse at the interface of two string described in the previous problem. In addition to the net disturbances being equal at the junction, the slope of the net disturbances must also be equal at the junction at all times. Given that p1 = 4.0 g/m, H2 = 9.0 g/m and Aj = 0.50 cm find 2. A, (Answer: -0.10 cm) and 3. Ay. (Answer: 0.40 cm)please I need to show all work step by step problems 2 and 3arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
What is Torque? | Physics | Extraclass.com; Author: Extraclass Official;https://www.youtube.com/watch?v=zXxrAJld9mo;License: Standard YouTube License, CC-BY