
Concept explainers
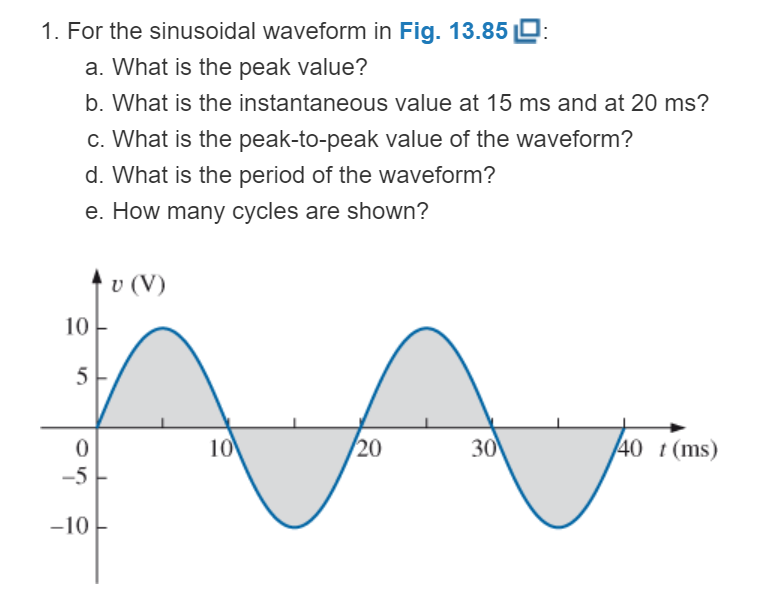
For the sinusoidal waveform in Fig. 13.85:
a. What is the peak value?
b. What is the instantaneous value at 15 ms and at 20 ms?
c. What is the peak-to-peak value of the waveform?
d. What is the period of the waveform?
e. How many cycles are shown?
(a)
Peak value of sinusoidal signal.
Answer to Problem 1P
The peak value is
Explanation of Solution
Calculation:
Peak value is the maximum value of an alternating quantity over one cycle duration.
So peak value is
Conclusion:
Thus, peak value is
(b)
Instantaneous value at
Answer to Problem 1P
The Instantaneous value at
Explanation of Solution
Calculation:
Instantaneous value is the valueof an alternating quantity at a particular value of time in a cycle.
So Instantaneous value at
Conclusion:
Thus, Instantaneous value at
(c)
Peak-to-peak value of sinusoidal signal.
Answer to Problem 1P
The peak-to-peak value of sinusoidal signal is
Explanation of Solution
Calculation:
Peak to peak value is the difference in the value of positive peak and negative peak of a waveform.
Write the expression for peak to peak value.
Here,
Substitute
Conclusion:
Thus, Peak-to-peak value of sinusoidal signal is
(d)
Value of period of the waveform.
Answer to Problem 1P
The value of period of the wave form is
Explanation of Solution
Calculation:
Period is the time taken by a waveform to complete its one cycle.
Waveform completes its one cycle in
Conclusion:
Thus, value of period of the wave form is
(e)
Value of number of cycles.
Answer to Problem 1P
The value of total number of cycle is
Explanation of Solution
Calculation:
There is
Conclusion:
Thus, value of total number of cycle is
Want to see more full solutions like this?
Chapter 13 Solutions
Introductory Circuit Analysis (13th Edition)
- I need Integration of equations S₁ (w) = In (|w] + 1)arrow_forwardFor the area shown in the figure, write the limits of integration using both the vertical and horizontal cross-sections, then evaluate the integrals. . Find the Fourier expression of the following periodic function 3 -3-2xarrow_forwardI need a solution from an expert without artificial intelligence. Choose the correct answer: 1. In AMI code, the shapes of "1" and "O" are, bit dependent, not related to each other). 2. In FDM the guard band is used to decrease, maintain, not related to). 3. Higher number of levels in PCM produces, (the same, opposite to each other, next the overlap between FDM signals. (increase, (higher quantization error, less number of bits per sample, lower quantization error, the same number of bits per sample). Fe Av 4. If the maximum shift in frequency is 70 kHz and the minimum deviation in frequency of the actual signal is 109.93 MHz, what is the carrier frequency? (110 MHz, 110 kHz, 107 kHz, 102 MHz) 5. TDM of signals requires them to have the same amplitude, sampling frequency, energy). 6. In standard AM, the last step in the transmitter is subtracting, multiplying, dividing). . In digital carrier systems, PSK). (maximum frequency, maximum the carrier signal. (adding, has higher bandwidth.…arrow_forward
- Need Handwritten step by step solution. Do not use chatgpt or AIarrow_forwardA linear electrical load draws 11 A at a 0.72 lagging power factor./1 153. When a capacitor is connected, the line current dropped to 122 A and the power factor improved to 0.98 lagging. Supply frequency is 50 Hz. a. Let the current drawn from the source before and after introduction of the capacitor be 11 and 12 respectively. Take the source voltage as the reference and express 11 and 12 as vector quantities in polar form. b. Obtain the capacitor current, IC = 12 - 11, graphically as well as using complex number manipulation. Compare the results. c. Express the waveforms of the source current before (11(t)) and after (12(t)) introduction of the capacitor in the form Im sin(2лft + 0). Hand sketch them on the same graph. Clearly label your plots. d. Analytically solve i2(t) – i1(t) using the theories of trigonometry to obtain the capacitor current in the form, ¡C(t) = ICm sin(2πft + OC). Compare the result with the result in Part b.arrow_forwardTransmission line data:Data:• Active power of the load (P): 50 kW• Power factor of the load (PF): 0.8 (lagging)• Line-to-line voltage at the load (V_LC): 13.8 kV• Line resistance (R): 2 Ω• Line inductance (L): 0.8 H• Line capacitance (C): 0.0003 F• Required series compensation: 60% of the line impedance.• Line length: 250 kmDetermine:1. Characteristic impedance and propagation constant.2. The generalized long line constants A, B, C, D.3. Total voltage, current and power at the generating end.4. Voltage regulation.5. Parameters A, B, C, D of the compensation circuit.6. New generalized constants of the power system afterseries compensation.7. Conclusion of the results obtained.arrow_forward
- 3.18 In a single-phase half-wave ac-dc converter, the average value of the load current is 1.78 A. If the converter is operated from a 240 V, 50 Hz supply and if the average value of the output voltage is 27% of the maximum possible value, calculate the following, assume the load to be resistive. (a) Load resistance (b) Firing angle (c) Average output voltage (d) The rms load voltage (e) The rms load current (f) DC power (g) AC power (h) Rectifier efficiency (i) Form factor (j) Ripple factorarrow_forwardTo find the Fourier series for the periodic function f(x) = 2 -2 when π < x < 0 - when 0 < x < πarrow_forwardDon't use ai to answer I will report you answerarrow_forward
- Don't use ai to answer I will report you answerarrow_forwardDisassemmble In another way f(t) = [sin(200πt) - cos(300πt)]2arrow_forward☑ 口 ☐ : Homework help starts here! Home | bartleby → https://www.bartleby.com Answered: Decompose using relationships 3 S(+) = 50 sin 3 (500πiz) | bartleby ASK AN EXPERT √ MATH SOLVER Decompose using relationships 3 S(+) = 50 sin 3 (500... Steps "Disassemble in another way." f(+)= 50 Sin³ (500+) Step 1 To decompose f(t)=50 Sin³ (500x+), use trigonometric indentity for Sin³ (e) Sin³ (0)- 3 Sin (e)-Sin (30) 4 Step2: Apply indentity to f(t). f(+)= 50 Sin³ (500+) = 50. 3 Sin (500+) - Sin (3*500π+) = 50. = = 12.5 4 3 Sin (500+)-Sin (1500+) 4 [3 Sin (580x+)-Sin (1500x+)] 37.5 Sin (500+)-12.5 Sin (1500π+) final decomposed form is, PM 05:2 19/12/2024 દ ))^ C W E × م اكتب هنا للبحثarrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





