Chapter 13, Problem 12RQ

When a fluid flows around an object, it creates a force, called the drag force, that pulls on the object. The coefficient of drag (C_d) is a dimensionless number that describes the relationship between the force created and the fluid and object properties, given as

$C_d=\frac{F_D}{\frac{1}{2}\rho {\upsilon }^2{A}_P}$

Where F_D is drag force, ρ is the fluid density, and υ is the velocity of the object relative to the fluid. The area of the object the force acts upon is A_P, and for spheres is given by the area of a circle. The Reynolds number in this situation is written as

$\mathrm{Re}=\frac{D_P\rho \upsilon }{\mu }$

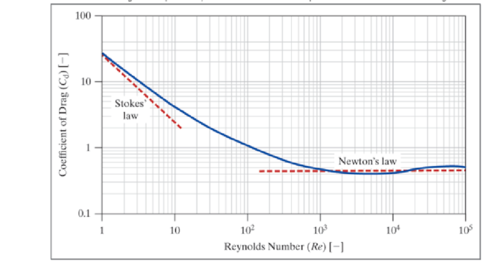
where D_P is the diameter of the object the force acts upon. The following chart shows this relationship. The dashed lines show the predicted theories of Stokes and Newton compared to the solid line of actual results.

1. a. If the Reynolds number is 500, what is the coefficient of drag?
2. b. If the coefficient of drag is 2, what is the Reynolds number?

   Ethylene glycol has a dynamic viscosity of 9.13 centipoise and a specific gravity of 1.109.

3. c. If the fluid flows around a sphere of diameter 1 centimeter travelling at a velocity of 2.15 centimeters per second, determine the drag force on the particle in units of newtons. (Hint: First determine the Reynolds number.)
4. d. If a coefficient of drag of 10 is produced, what is the diameter of the particle? Assume the fluid moving at 1 centimeter per second (Hint: First determine the Reynolds number.)