Chapter 12, Problem 76SE

a.

To determine

Find the regression line for the variables fracture toughness $\left(y\right)$ and mode-mixity angle $\left(x\right)$.

Test whether there is enough evidence to conclude that the predictor variable mode-mixity angle is useful for predicting the value of the response variable fracture toughness.

Answer to Problem 76SE

The regression line for the variables fracture toughness $\left(y\right)$ and mode-mixity angle $\left(x\right)$ is $\underset{\_}{\stackrel{⌢}{y}=-115+38.07x}$.

There is sufficient evidence to conclude that the predictor variable mode-mixity angle is useful for predicting the value of the response variable fracture toughness.

Explanation of Solution

Given info:

The data represents the values of the variables fracture toughness $\left(y\right)$ and mode-mixity angle $\left(x\right)$ for a sample of sandwich panels. The variable fracture toughness is measured in $\left(\frac{\text{N}}{\text{m}}\right)$ and the variable mode-mixity angle is measured in degrees.

Calculation:

Linear regression model:

A linear regression model is given as $\widehat{y}=b_0+b_{1}x$ where be the predicted values of response variable and x be the predictor variable. The $b_1$ be the slope and $b_0$ be the intercept of the line.

A linear regression model is given as $\widehat{y}={\widehat{\beta }}_0+{\widehat{\beta }}_{1}x$ where $\widehat{y}$ be the predicted values of response variable and x be the predictor variable. The ${\widehat{\beta }}_1$ be the estimate of slope and ${\widehat{\beta }}_0$ be the estimate of intercept of the line.

Regression:

Software procedure:

Step by step procedure to obtain regression equation using MINITAB software is given as,

• Choose Stat > Regression > Fit Regression Line.
• In Response (Y), enter the column of Fracture toughness.
• In Predictor (X), enter the column of Mode-mixity angle.
• Click OK.

The output using MINITAB software is given as,

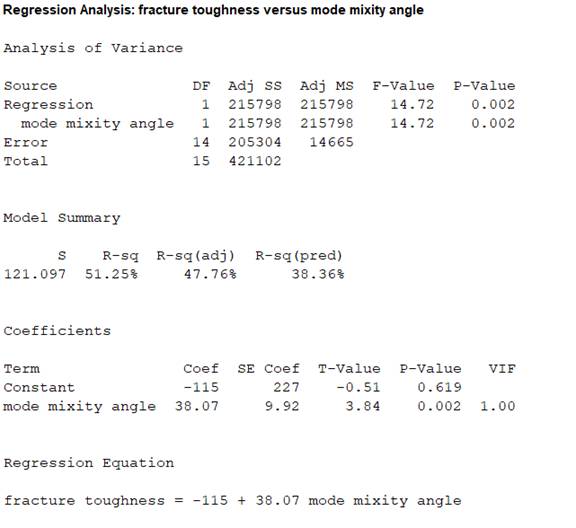
From the MINITAB output, the regression line is $\stackrel{⌢}{y}=-115+38.07x$.

Thus, the regression line for the variables fracture toughness $\left(y\right)$ and mode-mixity angle $\left(x\right)$ is $\underset{\_}{\stackrel{⌢}{y}=-115+38.07x}$.

Interpretation:

The slope estimate implies an increase in fracture toughness by 38.07 $\left(\frac{\text{N}}{\text{m}}\right)$ for every 1 degree increase in mode-mixity angle.

The test hypotheses are given below:

Null hypothesis:

$H_0:{\beta }_1=0$

That is, there is no useful relationship between the variables fracture toughness $\left(y\right)$ and mode-mixity angle $\left(x\right)$.

Alternative hypothesis:

$H_1:{\beta }_1\ne 0$

That is, there is useful relationship between the variables fracture toughness $\left(y\right)$ and mode-mixity angle $\left(x\right)$.

T-test statistic:

The test statistic is,

$t=\frac{{\widehat{\beta }}_1-{\beta }_1}{s_{{\widehat{\beta }}_1}}\sim t\left(n-2\right)$

From the MINITAB output, the test statistic is 3.84 and the P-value is 0.002.

Thus, the value of test statistic is 3.84 and P-value is 0.002.

Level of significance:

Here, level of significance is not given.

So, the prior level of significance $\alpha =0.05$ can be used.

Decision rule based on p-value:

If $P\text{-value}\le \alpha$, then reject the null hypothesis $H_0$.

If $P\text{-value}>\alpha$, then fail to reject the null hypothesis $H_0$.

Conclusion:

The P-value is 0.002 and $\alpha$ value is 0.05.

Here, P-value is less than the $\alpha$ value.

That is $0.002\left(=p\right)<0.05\left(=\alpha \right)$.

By the rejection rule, reject the null hypothesis.

Thus, there is enough evidence to conclude that the predictor variable mode-mixity angle is useful for predicting the value of the response variable fracture toughness.

b.

To determine

Test whether there is enough evidence to conclude that the change in fracture toughness associated with 1 degree increase in mode-mixity angle is greater than 50$\left(\frac{\text{N}}{\text{m}}\right)$.

Answer to Problem 76SE

There is no sufficient evidence to conclude that the change in fracture toughness associated with 1 degree increase in mode-mixity angle is greater than 50$\left(\frac{\text{N}}{\text{m}}\right)$.

Explanation of Solution

Calculation:

From the MINITAB output obtained in part (a), the slope coefficient of the regression equation is $b_1={\widehat{\beta }}_1=38.07$.

Here, ${\widehat{\beta }}_1$ be the slope of the sample regression line and ${\beta }_1$ is the slope of the population regression line.

Claim:

Here, the claim is that the true average change in the fracture toughness associated with 1 degree increase in mode-mixity angle is greater than 50$\left(\frac{\text{N}}{\text{m}}\right)$.

The test hypotheses are given below:

Null hypothesis:

$H_0:{\beta }_1\le 50$

That is, the average change in the fracture toughness associated with 1 degree increase in mode-mixity angle is less than or equal to 50$\left(\frac{\text{N}}{\text{m}}\right)$.

Alternative hypothesis:

$H_1:{\beta }_1>50$

That is, the average change in the fracture toughness associated with 1 degree increase in mode-mixity angle is greater than 50$\left(\frac{\text{N}}{\text{m}}\right)$.

Test statistic:

The test statistic is,

$t=\frac{{\widehat{\beta }}_1-{\beta }_1}{s_{{\widehat{\beta }}_1}}\sim t\left(n-2\right)$

Degrees of freedom:

The number of concrete beams that are sampled is $n=16$

The degrees of freedom is,

$\begin{array}{c}d.f=n-2\\ =16-2\\ =14\end{array}$

Thus, the degree of freedom is 14.

Level of significance:

Here, level of significance is not given.

So, the prior level of significance $\alpha =0.05$ can be used.

Critical value:

Software procedure:

Step by step procedure to obtain the critical value using the MINITAB software:

• Choose Graph > Probability Distribution Plot choose View Probability > OK.
• From Distribution, choose ‘t’ distribution and enter 14 as degrees of freedom.
• Click the Shaded Area tab.
• Choose Probability Value and Right Tail for the region of the curve to shade.
• Enter the Probability value as 0.05.
• Click OK.

Output using the MINITAB software is given below:

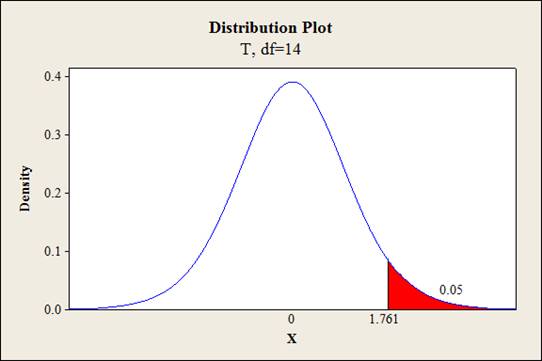
From the output, the critical value is 1.761.

Thus, the critical value is $\left(t_{{}_{0.05,14}}\right)=1.761$.

From the MINITAB output obtained in part (a), the estimate of error standard deviation of slope coefficient is $s_{{\widehat{\beta }}_1}=9.92$.

Test statistic under null hypothesis:

Under the null hypothesis, the test statistic is obtained as follows:

$\begin{array}{c}t=\frac{{\widehat{\beta }}_1-{\beta }_1}{s_{{\widehat{\beta }}_1}}\\ =\frac{38.07-50}{9.92}\\ =-1.2026\end{array}$

Thus, the test statistic is -1.2026.

Decision criteria for the classical approach:

If $t>t_{\alpha }\left(\text{test}\text{statistic}\text{> critical}\text{value}\right)$, then reject the null hypothesis $\left(H_0\right)$.

Conclusion:

Here, the test statistic is -1.2026 and critical value is 1.761.

The t statistic is less than the critical value.

That is, $-1.2026\left(\text{=test statistic}\right)<1.761\left(=\text{critical value}\right)$

Thus, the decision rule is, failed to reject the null hypothesis.

Hence, the average change in the fracture toughness associated with 1 degree increase in mode-mixity angle is less than or equal to 50$\left(\frac{\text{N}}{\text{m}}\right)$.

Therefore, there is no sufficient evidence to conclude that the change in fracture toughness associated with 1 degree increase in mode-mixity angle is greater than 50$\left(\frac{\text{N}}{\text{m}}\right)$

c.

To determine

Explain whether the new observations of the variable mode-mixity angle give more precise estimate of slope coefficient than the actual observations.

Answer to Problem 76SE

No, the new observations of the variable mode-mixity angle do not give more precise estimate of slope coefficient than the actual observations.

Explanation of Solution

Given info:

The data represents the new values of the variable mode-mixity angle, at which the response variable fracture toughness is predicted.

Calculation:

Confidence interval:

The general formula for the confidence interval for the slope of the regression line is,

$CI={\widehat{\beta }}_1\pm t_{a/2,\left(n-2\right)}\times s_{{\widehat{\beta }}_1}$

Where, ${\widehat{\beta }}_1$ be the slope of the sample regression line, $s_{{\widehat{\beta }}_1}$ be the estimate of error standard deviation of slope coefficient.

The precision of the confidence interval increases with the decrease in the error standard deviation of the slope.

That is, the precision will be high for lower value of $s_{{\widehat{\beta }}_1}$.

Error sum of square: (SSE)

The variation in the observed values of the response variable that is not explained by the regression is defined as the regression sum of squares. The formula for error sum of square is $SSE={{\displaystyle \sum _i\left(y_i-\widehat{y}\right)}}^2$ where $y_i$ be the predicted value of the i^th observation and $\overline{y}$ be the predicted value for the i^th observation.

Estimate of error standard deviation of slope coefficient:

The general formula for the estimate of error standard deviation of slope coefficient is,

${\sigma }_{{\widehat{\beta }}_1}=\frac{\sigma }{\sqrt{S_{xx}}}$,

The defining formula for $S_{\text{xx}}$ is,

$S_{xx}={\displaystyle \sum _i{x}_i^2}-\frac{{\left({\displaystyle \sum _i{x}_i}\right)}^2}{n}$

Here, the estimate of error standard deviation of slope coefficient depends on the value of $S_{\text{xx}}$. Since the population standard deviation remains same for both the experiments.

The estimate of error standard deviation of slope coefficient decreases with the increase in the value of $S_{\text{xx}}$. And the precision increases with the decrease in the error standard deviation.

The margin of error is product of critical value and standard error of the statistic. The higher width of the confidence interval indicates larger standard error of statistic. Hence, the margin of error also increases.

Therefore, the width of the confidence interval decreases with the decrease in value of error standard deviation. In other words it can be said that the precision decreases with the decrease in the value of $S_{xx}$.

$S_{\text{xx}}$ for old observations:

The value of $S_{\text{xx}}$ is obtained as follows:

$i$	$x_i$	$x_i^2$
1	16.52	272.9104
2	17.53	307.3009
3	18.05	325.8025
4	18.05	325.8025
5	22.39	501.3121
6	23.89	570.7321
7	25.50	650.25
8	24.89	619.5121
9	23.48	551.3104
10	24.98	624.0004
11	25.55	652.8025
12	25.90	670.81
13	22.65	513.0225
14	23.69	561.2161
15	24.15	583.2225
16	24.45	597.8025
Total	${\displaystyle \sum _i{x}_i}=361.67$	${\displaystyle \sum _i{x}_i^2}=8,327.81$

Here, ${\displaystyle \sum _i{x}_i^2}=8,327.81$, ${\displaystyle \sum _i{x}_i}=361.67$ and $n=16$.

Thus, the value of $S_{xx\left(1\right)}$ is,

$\begin{array}{c}{S}_{xx\left(1\right)}={\displaystyle \sum _i{x}_i^2}-\frac{{\left({\displaystyle \sum _i{x}_i}\right)}^2}{n}\\ =8,327.81-\frac{{\left(361.67\right)}^2}{16}\\ =8,327.81-8,175.324\\ =152.486\end{array}$

Hence, the covariance is $S_{xx\left(1\right)}=152.486$

$S_{\text{xx}}$ for new observations:

The value of $S_{xx\left(2\right)}$ is obtained as follows:

$i$	$x_i$	$x_i^2$
1	16	256
2	16	256
3	18	324
4	18	324
5	20	400
6	20	400
7	20	400
8	20	400
9	22	484
10	22	484
11	22	484
12	22	484
13	24	576
14	24	576
15	26	676
16	26	676
Total	${\displaystyle \sum _i{x}_i}=336$	${\displaystyle \sum _i{x}_i^2}=7,200$

Here, ${\displaystyle \sum _i{x}_i^2}=7,200$, ${\displaystyle \sum _i{x}_i}=336$ and $n=16$.

Thus, the value of $S_{xx\left(2\right)}$ is,

$\begin{array}{c}{S}_{xx\left(2\right)}={\displaystyle \sum _i{x}_i^2}-\frac{{\left({\displaystyle \sum _i{x}_i}\right)}^2}{n}\\ =7,200-\frac{{\left(336\right)}^2}{16}\\ =7,200-7,056\\ =144\end{array}$

Hence, the covariance is $S_{xx\left(2\right)}=144$

The value of $S_{\text{xx}}$ is higher for old observations than for new observations.

That is, $152.486>144$

Hence, the estimate of error standard deviation of slope coefficient is lower for old observations.

Therefore, the precision is high for old observations.

Thus, the new observations of the variable mode-mixity angle do not give more precise estimate of slope coefficient than the actual observations.

d.

To determine

Find the interval estimate for the true mean fracture toughness of all sandwich panels with 18 degrees mode-mixity angle.

Find the prediction interval of fracture toughness for a single sandwich panel of 18 degrees mode-mixity angle.

Find the interval estimate for the true mean fracture toughness of all sandwich panels with 22 degrees mode-mixity angle.

Find the prediction interval of fracture toughness for a single sandwich panel of 22 degrees mode-mixity angle.

Answer to Problem 76SE

The 95% specified confidence interval for the true mean fracture toughness of all sandwich panels with 18 degrees mode-mixity angle is $\underset{\_}{\left(453.6507,686.8693\right)}$.

The 95% prediction interval of fracture toughness for a single sandwich panel with 18 degrees mode-mixity angle is $\underset{\_}{\left(285.5331,854.9869\right)}$.

The 95% specified confidence interval for the true mean fracture toughness of all sandwich panels with 22 degrees mode-mixity angle is $\underset{\_}{\left(656.3689,788.7111\right)}$.

The 95% prediction interval of fracture toughness for a single sandwich panel with 22 degrees mode-mixity angle is $\underset{\_}{\left(454.491,990.589\right)}$.

Explanation of Solution

Calculation:

Here, the regression equation is $\stackrel{⌢}{y}=-115+38.07x$. Where y represents the variable fracture toughness and x represents the variable mode-mixity angle.

Expected fracture toughness when the mode-mixity angle is 18 degrees:

The expected fracture toughness with 18 degrees mode-mixity angle is obtained as follows:

$\begin{array}{c}{\mu }_{\widehat{y}}=-115+38.07x\\ =-115+38.07\times 18\\ =570.26\end{array}$

Thus, the expected fracture toughness with 18 degrees mode-mixity angle is 570.26.

95% confidence interval of true mean fracture tough for an angle of 18 degrees:

The general formula for the $\left(1-\alpha \right)$% confidence interval for the conditional mean at $x=x_p$ is,

$CI={\mu }_{\widehat{y}}\pm t_{\left(\frac{\alpha }{2},n-2\right)}s\sqrt{\frac{1}{n}+\frac{{\left(x_p-\overline{x}\right)}^2}{S_{\text{xx}}}}$

Where, ${\widehat{y}}_p$ be the point estimate for the conditional mean of the response variable at $x=x_p$, and $S_{\text{xx}}={\displaystyle \sum _i{x}_i^2}-\frac{{\left({\displaystyle \sum _i{x}_i}\right)}^2}{n}$.

From the MINITAB output in part (a), the value of the standard error of the estimate is $s=121.097$.

The value of $S_{\text{xx}}$ is obtained as follows:

$i$	$x_i$	$x_i^2$
1	16.52	272.9104
2	17.53	307.3009
3	18.05	325.8025
4	18.05	325.8025
5	22.39	501.3121
6	23.89	570.7321
7	25.50	650.25
8	24.89	619.5121
9	23.48	551.3104
10	24.98	624.0004
11	25.55	652.8025
12	25.90	670.81
13	22.65	513.0225
14	23.69	561.2161
15	24.15	583.2225
16	24.45	597.8025
Total	${\displaystyle \sum _i{x}_i}=361.67$	${\displaystyle \sum _i{x}_i^2}=8,327.81$

Here, ${\displaystyle \sum _i{x}_i^2}=8,327.81$, ${\displaystyle \sum _i{x}_i}=361.67$ and $n=16$.

The mean mode-mixity angle is,

$\begin{array}{c}\overline{x}=\frac{{\displaystyle \sum x_i}}{n}\\ =\frac{361.67}{16}\\ =22.6044\end{array}$

Thus, the mean mode-mixity angle is $\underset{\_}{\overline{x}=22.6044}$.

Covariance term $S_{\text{xx}}$:

Thus, the value of $S_{\text{xx}}$ is,

$\begin{array}{c}{S}_{xx\left(1\right)}={\displaystyle \sum _i{x}_i^2}-\frac{{\left({\displaystyle \sum _i{x}_i}\right)}^2}{n}\\ =8,327.81-\frac{{\left(361.67\right)}^2}{16}\\ =8,327.81-8,175.324\\ =152.486\end{array}$

Hence, the covariance is $S_{xx\left(1\right)}=152.486$

Since, the level of confidence is not specified. The prior confidence level 95% can be used.

Critical value:

For 95% confidence level,

$\begin{array}{c}1-\alpha =1-0.95\\ \alpha =0.05\\ \frac{\alpha }{2}=\frac{0.05}{2}\\ =0.025\end{array}$

Degrees of freedom:

The sample size is $n=16$

The degrees of freedom is,

$\begin{array}{c}d.f=n-2\\ =16-2\\ =14\end{array}$

From Table A.5 of the t-distribution in Appendix A, the critical value corresponding to the right tail area 0.025 and 14 degrees of freedom is 2.145.

Thus, the critical value is $\left(t_{{}_{\frac{\alpha }{2},14}}\right)=2.145$.

The 95% confidence interval is,

$\begin{array}{c}C.I={\mu }_{\widehat{y}}-t_{\left(\frac{\alpha }{2},n-2\right)}s\sqrt{\frac{1}{n}+\frac{{\left(x_p-\overline{x}\right)}^2}{S_{\text{xx}}}}\le {\mu }_y\le {\mu }_{\widehat{y}}+t_{\left(\frac{\alpha }{2},n-2\right)}s\sqrt{\frac{1}{n}+\frac{{\left(x_p-\overline{x}\right)}^2}{S_{\text{xx}}}}\\ =\left(570.26\pm 2.145\times 121.097\sqrt{\frac{1}{16}+\frac{{\left(18-22.6044\right)}^2}{152.486}}\right)\\ =\left(570.26\pm 116.6093\right)\\ \simeq \left(453.6507,686.8693\right)\end{array}$

Thus, the 95% specified confidence interval for the true mean fracture toughness of all sandwich panels with 18 degrees mode-mixity angle is $\underset{\_}{\left(453.6507,686.8693\right)}$.

Interpretation:

There is 95% confident that, the true mean fracture toughness of all sandwich panels with 18 degrees mode-mixity angle lies between 453.6507 and 686.8693.

95% prediction interval of fracture tough for an angle of 18 degrees:

Prediction interval for a single future value:

Prediction interval is used to predict a single value of the focus variable that is to be observed at some future time. In other words it can be said that the prediction interval gives a single future value rather than estimating the mean value of the variable.

The general formula for $\left(1-\alpha \right)$% prediction interval for the conditional mean at $x=x_p$ is,

$P.I={\widehat{y}}_p\pm t_{\frac{\alpha }{2}}s\sqrt{1+\frac{1}{n}+\frac{{\left(x_p-{\displaystyle \sum _i\frac{x_i}{n}}\right)}^2}{S_{\text{xx}}}}$

where ${\widehat{y}}_p$ be the predicted value of the response variable at $x=x_p$ and $S_{\text{xx}}={\displaystyle \sum _i{x}_i^2}-\frac{{\left({\displaystyle \sum _i{x}_i}\right)}^2}{n}$

The 95% prediction interval is,

$\begin{array}{c}P.I={\widehat{y}}_p\pm t_{\frac{\alpha }{2}}s\sqrt{1+\frac{1}{n}+\frac{{\left(x_p-\overline{x}\right)}^2}{S_{\text{xx}}}}\\ =570.26\pm \left(2.145\right)\left(121.097\right)\sqrt{1+\frac{1}{16}+\frac{{\left(18-22.6044\right)}^2}{154.486}}\\ =570.26\pm 284.9869\\ \simeq \left(285.5331,854.9869\right)\end{array}$

Thus, the 95% prediction interval of fracture toughness for a single sandwich panel with 18 degrees mode-mixity angle is $\underset{\_}{\left(285.5331,854.9869\right)}$.

Interpretation:

For repeated samples, there is 95% confident that the fracture toughness for a single sandwich panel with 18 degrees mode-mixity angle lies between 285.5331 and 854.9569.

Expected fracture toughness when the mode-mixity angle is 22 degrees:

The expected fracture toughness with 22 degrees mode-mixity angle is obtained as follows:

$\begin{array}{c}{\mu }_{\widehat{y}}=-115+38.07x\\ =-115+38.07\times 22\\ =722.54\end{array}$

Thus, the expected fracture toughness with 22 degrees mode-mixity angle is 722.54.

95% confidence interval of true mean fracture tough for an angle of 22 degrees:

The 95% confidence interval is,

$\begin{array}{c}C.I={\mu }_{\widehat{y}}-t_{\left(\frac{\alpha }{2},n-2\right)}s\sqrt{\frac{1}{n}+\frac{{\left(x_p-\overline{x}\right)}^2}{S_{\text{xx}}}}\le {\mu }_y\le {\mu }_{\widehat{y}}+t_{\left(\frac{\alpha }{2},n-2\right)}s\sqrt{\frac{1}{n}+\frac{{\left(x_p-\overline{x}\right)}^2}{S_{\text{xx}}}}\\ =\left(722.54\pm 2.145\times 121.097\sqrt{\frac{1}{16}+\frac{{\left(22-22.6044\right)}^2}{152.486}}\right)\\ =\left(722.54\pm 66.17111\right)\\ \simeq \left(656.3689,788.7111\right)\end{array}$

Thus, the 95% specified confidence interval for the true mean fracture toughness of all sandwich panels with 22 degrees mode-mixity angle is $\underset{\_}{\left(656.3689,788.7111\right)}$.

Interpretation:

There is 95% confident that, the true mean fracture toughness of all sandwich panels with 22 degrees mode-mixity angle lies between 656.3689 and 788.7111.

95% prediction interval of fracture tough for an angle of 22 degrees:

The 95% prediction interval is,

$\begin{array}{c}P.I={\widehat{y}}_p\pm t_{\frac{\alpha }{2}}s\sqrt{1+\frac{1}{n}+\frac{{\left(x_p-\overline{x}\right)}^2}{S_{\text{xx}}}}\\ =722.54\pm \left(2.145\right)\left(121.097\right)\sqrt{1+\frac{1}{16}+\frac{{\left(22-22.6044\right)}^2}{154.486}}\\ =722.54\pm 284.9869\\ \simeq \left(454.491,990.589\right)\end{array}$

Thus, the 95% prediction interval of fracture toughness for a single sandwich panel with 22 degrees mode-mixity angle is $\underset{\_}{\left(454.491,990.589\right)}$.

Interpretation:

For repeated samples, there is 95% confident that the fracture toughness for a single sandwich panel with 22 degrees mode-mixity angle lies between 454.491 and 990.589.