College Algebra (Collegiate Math)
College Algebra (Collegiate Math)
2nd Edition
ISBN: 9780077836344
Author: Julie Miller, Donna Gerken
Publisher: McGraw-Hill Education
bartleby

Videos

Textbook Question
Book Icon
Chapter 1.2, Problem 55PE

Consider a seesaw with two children of masses m 1 and m 2 on either side. Suppose that the position of the fulcrum (pivot point) is labeled as the origin, x 5 0. Further suppose that the position of each child relative to the origin is x 1 and x 2 , respectively. The seesaw will be in equilibrium if m 1 x 1 + m 2 x 2 = 0. Use this equation for Exercises 55–58.

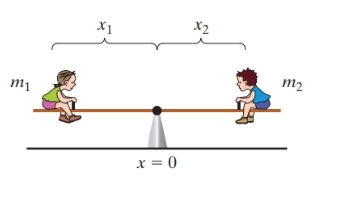
Chapter 1.2, Problem 55PE, Consider a seesaw with two children of masses and on either side. Suppose that the position of the

Find x 2 so that the system of masses is in equilibrium.

m 1 = 30  kg , x 1 = − 12  m and m 2 = 20  kg , x 2 = ?

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 1.2, Problem 54PE
Next
Chapter 1.2, Problem 56PE
Students have asked these similar questions
In Exercises 9–24, find the equation of each of the circles from the given information.
In Exercises 5–12, find the standard form of the equation of each hyperbola satisfying the given conditions. 5. Foci: (0, –3), (0, 3); vertices: (0, –1), (0, 1) 6. Foci: (0, –6), (0, 6); vertices: (0, -2), (0, 2) 7. Foci: (-4, 0), (4, 0); vertices: (-3, 0), (3,0) 8. Foci: (-7, 0), (7, 0); vertices: (-5, 0), (5,0) 9. Endpoints of transverse axis: (0, -6), (0, 6); asymptote: y = 2x 10. Endpoints of transverse axis: (-4,0), (4, 0); asymptote: y = 2r 11. Center: (4, -2); Focus: (7, -2); vertex: (6, -2) 12. Center: (-2, 1); Focus: (-2, 6); vertex: (-2, 4)
Find x such that the points A(x, 5), B(2, 3), and C(4, - 5) are collinear.

Chapter 1 Solutions

College Algebra (Collegiate Math)

Ch. 1.1 - Skill Practice 1 Solve. Ch. 1.1 - Skill Practice 2 Solve. y+52y24=y+73+1Ch. 1.1 - Skill Practice 3 To rent a storage unit, a...Ch. 1.1 - Skill Practice 4 Identify each equation as a...Ch. 1.1 - Skill Practice 5 Solve the equation and check the...Ch. 1.1 - Skill Practice 6 Solve the equation and check the...Ch. 1.1 - Skill Practice 7 Solve the equation....Ch. 1.1 - Skill Practice 8 Solve for the indicated...Ch. 1.1 - Skill Practice 9 Solve the equation for x....Ch. 1.1 - 1. An equation that can be written in the form,...
Ch. 1.1 - A linear equation is also called a...Ch. 1.1 - A __________ to an equation is the value of the...Ch. 1.1 - A _________equation is one that is true for some...Ch. 1.1 - 5. An_________ is an equation that is true for...Ch. 1.1 - A ___________ is an equation that is false for all...Ch. 1.1 - 7. A ___________equation is an equation in which...Ch. 1.1 - 8. If an equation has no solution, then the...Ch. 1.1 - For Exercises 910, determine if the equation is...Ch. 1.1 - For Exercises 9–10, determine if the equation is...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 11–30, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 11–30, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 11–30, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - For Exercises 11–30, solve the equation. (See...Ch. 1.1 - For Exercises 11–30, solve the equation. (See...Ch. 1.1 - For Exercises 1130, solve the equation. (See...Ch. 1.1 - In the mid-nineteenth century, explorers used the...Ch. 1.1 - For a recent year, the cost C(in$) for tuition and...Ch. 1.1 - 33. The annual per capita spending for...Ch. 1.1 - Prob. 34PECh. 1.1 - A motorist drives on State Road 417 to and from...Ch. 1.1 - A subway ride is $2.25 per ride. a. Write a model...Ch. 1.1 - 37. Helene considers two jobs. One pays $45,000/yr...Ch. 1.1 - Tasha considers two sales jobs for different...Ch. 1.1 - For Exercises 3944, identify the equation as a...Ch. 1.1 - For Exercises 3944, identify the equation as a...Ch. 1.1 - For Exercises 3944, identify the equation as a...Ch. 1.1 - For Exercises 3944, identify the equation as a...Ch. 1.1 - For Exercises 39–44, identify the equation as a...Ch. 1.1 - For Exercises 3944, identify the equation as a...Ch. 1.1 - For Exercises 4548, determine the restrictions on...Ch. 1.1 - For Exercises 4548, determine the restrictions on...Ch. 1.1 - For Exercises 45–48, determine the restrictions on...Ch. 1.1 - For Exercises 45–48, determine the restrictions on...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 49–66, solve the equation. (See...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 49–66, solve the equation. (See...Ch. 1.1 - For Exercises 49–66, solve the equation. (See...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 49–66, solve the equation. (See...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 4966, solve the equation. (See...Ch. 1.1 - For Exercises 49–66, solve the equation. (See...Ch. 1.1 - For Exercises 6788, solve for the specified...Ch. 1.1 - For Exercises 67–88, solve for the specified...Ch. 1.1 - For Exercises 67–88, solve for the specified...Ch. 1.1 - For Exercises 6788, solve for the specified...Ch. 1.1 - For Exercises 67–88, solve for the specified...Ch. 1.1 - For Exercises 67–88, solve for the specified...Ch. 1.1 - For Exercises 6788, solve for the specified...Ch. 1.1 - For Exercises 67–88, solve for the specified...Ch. 1.1 - For Exercises 6788, solve for the specified...Ch. 1.1 - For Exercises 67–88, solve for the specified...Ch. 1.1 - For Exercises 67–88, solve for the specified...Ch. 1.1 - For Exercises 6788, solve for the specified...Ch. 1.1 - For Exercises 67–88, solve for the specified...Ch. 1.1 - For Exercises 6788, solve for the specified...Ch. 1.1 - For Exercises 67–88, solve for the specified...Ch. 1.1 - For Exercises 6788, solve for the specified...Ch. 1.1 - For Exercises 67–88, solve for the specified...Ch. 1.1 - For Exercises 67–88, solve for the specified...Ch. 1.1 - For Exercises 6788, solve for the specified...Ch. 1.1 - For Exercises 6788, solve for the specified...Ch. 1.1 - For Exercises 6788, solve for the specified...Ch. 1.1 - For Exercises 6788, solve for the specified...Ch. 1.1 - For Exercises 89–102, solve the equation. 89. Ch. 1.1 - For Exercises 89102, solve the equation....Ch. 1.1 - For Exercises 89102, solve the equation....Ch. 1.1 - For Exercises 89102, solve the equation....Ch. 1.1 - For Exercises 89–102, solve the equation. 93. Ch. 1.1 - For Exercises 89102, solve the equation....Ch. 1.1 - For Exercises 89102, solve the equation....Ch. 1.1 - For Exercises 89102, solve the equation....Ch. 1.1 - For Exercises 89–102, solve the equation. 97. Ch. 1.1 - For Exercises 89102, solve the equation....Ch. 1.1 - For Exercises 89102, solve the equation....Ch. 1.1 - For Exercises 89102, solve the equation....Ch. 1.1 - For Exercises 89102, solve the equation....Ch. 1.1 - For Exercises 89102, solve the equation....Ch. 1.1 - Suppose that 40 deer are introduced in a protected...Ch. 1.1 - Prob. 104PECh. 1.1 - Prob. 105PECh. 1.1 - Prob. 106PECh. 1.1 - Prob. 107PECh. 1.1 - Prob. 108PECh. 1.1 - Prob. 109PECh. 1.1 - Prob. 110PECh. 1.1 - Explain why the equation x+1=x+2 has no solution.Ch. 1.1 - 112. Explain the difference in the process to...Ch. 1.1 - Prob. 113PECh. 1.1 - Prob. 114PECh. 1.1 - Prob. 115PECh. 1.1 - For Exercises 113116, find the value of a so that...Ch. 1.2 - Skill Practice 1 Franz borrowed a total of...Ch. 1.2 - Skill Practice 2 How much 4% acid solution should...Ch. 1.2 - Skill Practice 3 Rene drove from Miami to Orlando,...Ch. 1.2 - Prob. 4SPCh. 1.2 - Skill Practice 5 For the 104th Congress, there...Ch. 1.2 - Prob. 1PECh. 1.2 - Prob. 2PECh. 1.2 - Prob. 3PECh. 1.2 - Prob. 4PECh. 1.2 - Prob. 5PECh. 1.2 - Prob. 6PECh. 1.2 - Rocco borrowed a total of $5000 from two student...Ch. 1.2 - 8. Laura borrowed a total of $22,000 from two...Ch. 1.2 - Prob. 9PECh. 1.2 - Ebony bought a 5-yr Treasury note that paid the...Ch. 1.2 - 11. Ethanol fuel mixtures have “E” numbers that...Ch. 1.2 - A nurse mixes 60 cc of a 50% saline solution with...Ch. 1.2 - Prob. 13PECh. 1.2 - Prob. 14PECh. 1.2 - Two passengers leave the airport at Kansas City,...Ch. 1.2 - Prob. 16PECh. 1.2 - Prob. 17PECh. 1.2 - Prob. 18PECh. 1.2 - Prob. 19PECh. 1.2 - Prob. 20PECh. 1.2 - Prob. 21PECh. 1.2 - Prob. 22PECh. 1.2 - At a construction site, cement, sand, and gravel...Ch. 1.2 - The property tax on a $180,000 house is $1296. At...Ch. 1.2 - In addition to measuring a persons individual HDL...Ch. 1.2 - For a recent Congress, there were 10 more...Ch. 1.2 - When studying wildlife populations, biologists...Ch. 1.2 - 28. To estimate the number of bass in a lake, a...Ch. 1.2 - Prob. 29PECh. 1.2 - Suppose that a shallow earthquake occurs in which...Ch. 1.2 - 31. Suppose that a merchant buys a patio set from...Ch. 1.2 - Prob. 32PECh. 1.2 - Prob. 33PECh. 1.2 - Prob. 34PECh. 1.2 - Prob. 35PECh. 1.2 - Prob. 36PECh. 1.2 - 37. A vertical pole is placed in the ground at a...Ch. 1.2 - Prob. 38PECh. 1.2 - 39. A tank contains 40 L of a mixture of plant...Ch. 1.2 - Prob. 40PECh. 1.2 - 41. The perimeter of a rectangular lot of land is...Ch. 1.2 - Prob. 42PECh. 1.2 - 43. A contractor must tile a rectangular kitchen...Ch. 1.2 - Max and Molly plan to put down all-weather...Ch. 1.2 - Aliyah earned an $8000 bonus from her sales job...Ch. 1.2 - 46. Caitlin invested money in two mutual funds-a...Ch. 1.2 - Proportions are used in geometry with similar...Ch. 1.2 - Prob. 48PECh. 1.2 - Is it possible for the measures of the angles in a...Ch. 1.2 - Bob wants to change a $100 bill into an equal...Ch. 1.2 - Prob. 51PECh. 1.2 - One number is 25 more than another number. The...Ch. 1.2 - The sum of the digits of a two-digit number is 14....Ch. 1.2 - Prob. 54PECh. 1.2 - Consider a seesaw with two children of masses and...Ch. 1.2 - Consider a seesaw with two children of masses m1...Ch. 1.2 - Prob. 57PECh. 1.2 - Consider a seesaw with two children of masses and...Ch. 1.3 - Skill Practice 1 Write each expression in terms of...Ch. 1.3 - Skill Practice 2 Multiply or divide as indicated....Ch. 1.3 - Skill Practice 3 Simplify each expression and...Ch. 1.3 - Skill Practice 4 Simplify. a. i13 b. i103 c. i64...Ch. 1.3 - Prob. 5SPCh. 1.3 - Prob. 6SPCh. 1.3 - Skill Practice 7 Multiply. Write the result in the...Ch. 1.3 - Prob. 8SPCh. 1.3 - Prob. 1PECh. 1.3 - For a positive real number b, the value b=.Ch. 1.3 - 3. Given a complex number, the value of a is...Ch. 1.3 - Given a complex number a+ib, the expression aib is...Ch. 1.3 - For Exercises 5–22, write each expression in terms...Ch. 1.3 - For Exercises 522, write each expression in terms...Ch. 1.3 - Prob. 7PECh. 1.3 - For Exercises 522, write each expression in terms...Ch. 1.3 - For Exercises 5–22, write each expression in terms...Ch. 1.3 - For Exercises 522, write each expression in terms...Ch. 1.3 - Prob. 11PECh. 1.3 - For Exercises 5–22, write each expression in terms...Ch. 1.3 - For Exercises 5–22, write each expression in terms...Ch. 1.3 - Prob. 14PECh. 1.3 - For Exercises 5–22, write each expression in terms...Ch. 1.3 - For Exercises 5–22, write each expression in terms...Ch. 1.3 - For Exercises 522, write each expression in terms...Ch. 1.3 - Prob. 18PECh. 1.3 - For Exercises 522, write each expression in terms...Ch. 1.3 - Prob. 20PECh. 1.3 - For Exercises 5–22, write each expression in terms...Ch. 1.3 - For Exercises 522, write each expression in terms...Ch. 1.3 - For Exercises 23–28, determine the real and...Ch. 1.3 - For Exercises 2328, determine the real and...Ch. 1.3 - For Exercises 2328, determine the real and...Ch. 1.3 - For Exercises 23–28, determine the real and...Ch. 1.3 - For Exercises 23–28, determine the real and...Ch. 1.3 - For Exercises 2328, determine the real and...Ch. 1.3 - For Exercises 29–40, simplify each expression and...Ch. 1.3 - For Exercises 29–40, simplify each expression and...Ch. 1.3 - For Exercises 29–40, simplify each expression and...Ch. 1.3 - For Exercises 2940, simplify each expression and...Ch. 1.3 - For Exercises 29–40, simplify each expression and...Ch. 1.3 - Prob. 34PECh. 1.3 - For Exercises 2940, simplify each expression and...Ch. 1.3 - Prob. 36PECh. 1.3 - For Exercises 2940, simplify each expression and...Ch. 1.3 - Prob. 38PECh. 1.3 - For Exercises 2940, simplify each expression and...Ch. 1.3 - Prob. 40PECh. 1.3 - For Exercises 4144, simplify the powers of i. (See...Ch. 1.3 - Prob. 42PECh. 1.3 - Prob. 43PECh. 1.3 - Prob. 44PECh. 1.3 - For Exercises 45–68, perform the indicated...Ch. 1.3 - For Exercises 4568, perform the indicated...Ch. 1.3 - For Exercises 4568, perform the indicated...Ch. 1.3 - For Exercises 4568, perform the indicated...Ch. 1.3 - Prob. 49PECh. 1.3 - For Exercises 4568, perform the indicated...Ch. 1.3 - Prob. 51PECh. 1.3 - Prob. 52PECh. 1.3 - For Exercises 4568, perform the indicated...Ch. 1.3 - Prob. 54PECh. 1.3 - For Exercises 45–68, perform the indicated...Ch. 1.3 - Prob. 56PECh. 1.3 - For Exercises 45–68, perform the indicated...Ch. 1.3 - Prob. 58PECh. 1.3 - For Exercises 4568, perform the indicated...Ch. 1.3 - Prob. 60PECh. 1.3 - For Exercises 45–68, perform the indicated...Ch. 1.3 - Prob. 62PECh. 1.3 - For Exercises 4568, perform the indicated...Ch. 1.3 - Prob. 64PECh. 1.3 - For Exercises 4568, perform the indicated...Ch. 1.3 - For Exercises 4568, perform the indicated...Ch. 1.3 - Prob. 67PECh. 1.3 - For Exercises 45–68, perform the indicated...Ch. 1.3 - Prob. 69PECh. 1.3 - For Exercises 6972, for each given number, (a)...Ch. 1.3 - Prob. 71PECh. 1.3 - For Exercises 6972, for each given number, (a)...Ch. 1.3 - Prob. 73PECh. 1.3 - For Exercises 7388, perform the indicated...Ch. 1.3 - Prob. 75PECh. 1.3 - Prob. 76PECh. 1.3 - For Exercises 7388, perform the indicated...Ch. 1.3 - For Exercises 7388, perform the indicated...Ch. 1.3 - For Exercises 7388, perform the indicated...Ch. 1.3 - Prob. 80PECh. 1.3 - For Exercises 73–88, perform the indicated...Ch. 1.3 - For Exercises 7388, perform the indicated...Ch. 1.3 - Prob. 83PECh. 1.3 - For Exercises 7388, perform the indicated...Ch. 1.3 - Prob. 85PECh. 1.3 - Prob. 86PECh. 1.3 - Prob. 87PECh. 1.3 - Prob. 88PECh. 1.3 - Prob. 89PECh. 1.3 - Prob. 90PECh. 1.3 - Prob. 91PECh. 1.3 - Prob. 92PECh. 1.3 - Prob. 93PECh. 1.3 - Prob. 94PECh. 1.3 - Prob. 95PECh. 1.3 - Prob. 96PECh. 1.3 - Prob. 97PECh. 1.3 - Prob. 98PECh. 1.3 - Prob. 99PECh. 1.3 - Prob. 100PECh. 1.3 - Prob. 101PECh. 1.3 - Prob. 102PECh. 1.3 - Prob. 103PECh. 1.3 - Prob. 104PECh. 1.3 - Prob. 105PECh. 1.3 - Prob. 106PECh. 1.3 - For Exercises 105110, factor the expressions over...Ch. 1.3 - Prob. 108PECh. 1.3 - Prob. 109PECh. 1.3 - For Exercises 105110, factor the expressions over...Ch. 1.3 - Prob. 111PECh. 1.3 - Prob. 112PECh. 1.3 - Prob. 113PECh. 1.3 - Prob. 114PECh. 1.4 - Skill Practice 1 Solve the equations. a. b. Ch. 1.4 - Skill Practice 2 Solve the equations by using the...Ch. 1.4 - Skill Practice 3 Determine the value of n that...Ch. 1.4 - Prob. 4SPCh. 1.4 - Prob. 5SPCh. 1.4 - Prob. 6SPCh. 1.4 - Skill Practice 7 Solve the equation by applying...Ch. 1.4 - Skill Practice 8 Use the discriminant to determine...Ch. 1.4 - Prob. 9SPCh. 1.4 - Skill Practice 10 Solve for p. cp2dp=kCh. 1.4 - 1. A _________ equation is a second-degree...Ch. 1.4 - Prob. 2PECh. 1.4 - Prob. 3PECh. 1.4 - Prob. 4PECh. 1.4 - Prob. 5PECh. 1.4 - Prob. 6PECh. 1.4 - For Exercises 718, solve by applying the zero...Ch. 1.4 - For Exercises 718, solve by applying the zero...Ch. 1.4 - For Exercises 7–18, solve by applying the zero...Ch. 1.4 - For Exercises 718, solve by applying the zero...Ch. 1.4 - For Exercises 7–18, solve by applying the zero...Ch. 1.4 - For Exercises 7–18, solve by applying the zero...Ch. 1.4 - For Exercises 7–18, solve by applying the zero...Ch. 1.4 - For Exercises 7–18, solve by applying the zero...Ch. 1.4 - For Exercises 7–18, solve by applying the zero...Ch. 1.4 - For Exercises 718, solve by applying the zero...Ch. 1.4 - For Exercises 7–18, solve by applying the zero...Ch. 1.4 - For Exercises 7–18, solve by applying the zero...Ch. 1.4 - For Exercises 1930, solve by using the square root...Ch. 1.4 - Prob. 20PECh. 1.4 - For Exercises 19–30, solve by using the square...Ch. 1.4 - Prob. 22PECh. 1.4 - For Exercises 19–30, solve by using the square...Ch. 1.4 - Prob. 24PECh. 1.4 - Prob. 25PECh. 1.4 - For Exercises 1930, solve by using the square root...Ch. 1.4 - For Exercises 1930, solve by using the square root...Ch. 1.4 - Prob. 28PECh. 1.4 - For Exercises 1930, solve by using the square root...Ch. 1.4 - Prob. 30PECh. 1.4 - For Exercises 31–38, determine the value of n that...Ch. 1.4 - For Exercises 3138, determine the value of n that...Ch. 1.4 - Prob. 33PECh. 1.4 - Prob. 34PECh. 1.4 - For Exercises 31–38, determine the value of n that...Ch. 1.4 - Prob. 36PECh. 1.4 - Prob. 37PECh. 1.4 - Prob. 38PECh. 1.4 - For Exercises 3950, solve by completing the square...Ch. 1.4 - Prob. 40PECh. 1.4 - For Exercises 39–50, solve by completing the...Ch. 1.4 - For Exercises 39–50, solve by completing the...Ch. 1.4 - For Exercises 39–50, solve by completing the...Ch. 1.4 - Prob. 44PECh. 1.4 - For Exercises 39–50, solve by completing the...Ch. 1.4 - Prob. 46PECh. 1.4 - For Exercises 3950, solve by completing the square...Ch. 1.4 - Prob. 48PECh. 1.4 - For Exercises 39–50, solve by completing the...Ch. 1.4 - For Exercises 39–50, solve by completing the...Ch. 1.4 - For Exercises 5154, identify values of a, b, and c...Ch. 1.4 - Prob. 52PECh. 1.4 - For Exercises 5154, identify values of a, b, and c...Ch. 1.4 - Prob. 54PECh. 1.4 - For Exercises 55–70, solve by using the quadratic...Ch. 1.4 - For Exercises 5570, solve by using the quadratic...Ch. 1.4 - For Exercises 55–70, solve by using the quadratic...Ch. 1.4 - Prob. 58PECh. 1.4 - For Exercises 55–70, solve by using the quadratic...Ch. 1.4 - Prob. 60PECh. 1.4 - For Exercises 5570, solve by using the quadratic...Ch. 1.4 - Prob. 62PECh. 1.4 - For Exercises 5570, solve by using the quadratic...Ch. 1.4 - For Exercises 5570, solve by using the quadratic...Ch. 1.4 - Prob. 65PECh. 1.4 - Prob. 66PECh. 1.4 - For Exercises 55–70, solve by using the quadratic...Ch. 1.4 - Prob. 68PECh. 1.4 - Prob. 69PECh. 1.4 - For Exercises 5570, solve by using the quadratic...Ch. 1.4 - Prob. 71PECh. 1.4 - Prob. 72PECh. 1.4 - Prob. 73PECh. 1.4 - Prob. 74PECh. 1.4 - Prob. 75PECh. 1.4 - Prob. 76PECh. 1.4 - Prob. 77PECh. 1.4 - Prob. 78PECh. 1.4 - For Exercises 7996, solve the equation by using...Ch. 1.4 - Prob. 80PECh. 1.4 - For Exercises 7996, solve the equation by using...Ch. 1.4 - Prob. 82PECh. 1.4 - For Exercises 7996, solve the equation by using...Ch. 1.4 - For Exercises 79–96, solve the equation by using...Ch. 1.4 - Prob. 85PECh. 1.4 - For Exercises 7996, solve the equation by using...Ch. 1.4 - For Exercises 79–96, solve the equation by using...Ch. 1.4 - Prob. 88PECh. 1.4 - Prob. 89PECh. 1.4 - For Exercises 79–96, solve the equation by using...Ch. 1.4 - For Exercises 79–96, solve the equation by using...Ch. 1.4 - Prob. 92PECh. 1.4 - Prob. 93PECh. 1.4 - For Exercises 79–96, solve the equation by using...Ch. 1.4 - Prob. 95PECh. 1.4 - Prob. 96PECh. 1.4 - Prob. 97PECh. 1.4 - Prob. 98PECh. 1.4 - Prob. 99PECh. 1.4 - Prob. 100PECh. 1.4 - Prob. 101PECh. 1.4 - For Exercises 97104, (a) evaluate the discriminant...Ch. 1.4 - Prob. 103PECh. 1.4 - Prob. 104PECh. 1.4 - For Exercises 105118, solve for the indicated...Ch. 1.4 - Prob. 106PECh. 1.4 - For Exercises 105118, solve for the indicated...Ch. 1.4 - For Exercises 105–118, solve for the indicated...Ch. 1.4 - For Exercises 105118, solve for the indicated...Ch. 1.4 - Prob. 110PECh. 1.4 - Prob. 111PECh. 1.4 - Prob. 112PECh. 1.4 - For Exercises 105–118, solve for the indicated...Ch. 1.4 - For Exercises 105–118, solve for the indicated...Ch. 1.4 - Prob. 115PECh. 1.4 - Prob. 116PECh. 1.4 - Prob. 117PECh. 1.4 - Prob. 118PECh. 1.4 - Prob. 119PECh. 1.4 - Prob. 120PECh. 1.4 - Prob. 121PECh. 1.4 - Prob. 122PECh. 1.4 - Prob. 123PECh. 1.4 - Prob. 124PECh. 1.4 - Prob. 125PECh. 1.4 - Prob. 126PECh. 1.4 - Prob. 127PECh. 1.4 - For Exercises 123–132, write an equation with...Ch. 1.4 - Prob. 129PECh. 1.4 - Prob. 130PECh. 1.4 - Prob. 131PECh. 1.4 - Prob. 132PECh. 1.4 - Prob. 133PECh. 1.4 - Prob. 134PECh. 1.4 - Prob. 1PRECh. 1.4 - Prob. 2PRECh. 1.4 - Prob. 3PRECh. 1.4 - Prob. 4PRECh. 1.4 - Prob. 5PRECh. 1.4 - Prob. 6PRECh. 1.4 - For Exercises 18, identify the statement as an...Ch. 1.4 - For Exercises 1–8, identify the statement as an...Ch. 1.5 - Skill Practice 1 A box is to be formed by taking a...Ch. 1.5 - Skill Practice 2 A sail on a sailboat is in the...Ch. 1.5 - Skill Practice 3 A fireworks mortar is launched...Ch. 1.5 - Prob. 1PECh. 1.5 - 2. Write a formula for the area of a circle of...Ch. 1.5 - 3. Write a formula for the volume of a rectangular...Ch. 1.5 - Prob. 4PECh. 1.5 - For Exercises 512, refer to the geometry formulas...Ch. 1.5 - Prob. 6PECh. 1.5 - For Exercises 512, refer to the geometry formulas...Ch. 1.5 - Prob. 8PECh. 1.5 - For Exercises 5–12, refer to the geometry formulas...Ch. 1.5 - Prob. 10PECh. 1.5 - For Exercises 5–12, refer to the geometry formulas...Ch. 1.5 - For Exercises 512, refer to the geometry formulas...Ch. 1.5 - A rectangular garden covers 40yd2. The length is 2...Ch. 1.5 - A rectangular piece of carpet covers 200yd2. The...Ch. 1.5 - The height of a triangular truss is 8 ft less than...Ch. 1.5 - Prob. 16PECh. 1.5 - 17. a. Write an equation representing the fact...Ch. 1.5 - Prob. 18PECh. 1.5 - a. Write an equation representing the fact that...Ch. 1.5 - Prob. 20PECh. 1.5 - 21. On moving day, Guyton needs to rent a truck....Ch. 1.5 - 22. Lorene plans to make several open-topped boxes...Ch. 1.5 - Prob. 23PECh. 1.5 - Prob. 24PECh. 1.5 - Prob. 25PECh. 1.5 - The front face of a house is in the shape of a...Ch. 1.5 - Prob. 27PECh. 1.5 - Prob. 28PECh. 1.5 - The sail on a sailboat is in the shape of two...Ch. 1.5 - Prob. 30PECh. 1.5 - Prob. 31PECh. 1.5 - Prob. 32PECh. 1.5 - In a round-robin tennis tournament, each player...Ch. 1.5 - Prob. 34PECh. 1.5 - The population P of a culture of Pseudomonas...Ch. 1.5 - Prob. 36PECh. 1.5 - The distance d (in ft) required to stop a car that...Ch. 1.5 - Prob. 38PECh. 1.5 - For Exercises 3942, use the model s=12gt2+v0t+s0...Ch. 1.5 - For Exercises 39–42, use the model with or ....Ch. 1.5 - Prob. 41PECh. 1.5 - For Exercises 39–42, use the model with or ....Ch. 1.5 - Prob. 43PECh. 1.5 - An artist has been commissioned to make a stained...Ch. 1.5 - 45. A farmer has 160 yd of fencing material and...Ch. 1.5 - Prob. 46PECh. 1.6 - Skill Practice 1 Solve the equation....Ch. 1.6 - Skill Practice 2 Solve the equation. w4=27wCh. 1.6 - Prob. 3SPCh. 1.6 - Skill Practice 4 A fishing boat can travel 60 km...Ch. 1.6 - Skill Practice 5 Solve the equation. a. 5|24t|=50...Ch. 1.6 - Skill Practice 6 Solve the equation. a....Ch. 1.6 - Skill Practice 7 Solve the equation. Ch. 1.6 - Prob. 8SPCh. 1.6 - Skill Practice 9 Solve the equation. 2(x4)3/4=54Ch. 1.6 - Prob. 10SPCh. 1.6 - Prob. 11SPCh. 1.6 - Prob. 1PECh. 1.6 - Prob. 2PECh. 1.6 - The equation m2/3+10m1/3+9=0 is said to be in...Ch. 1.6 - Prob. 4PECh. 1.6 - For Exercises 5–20, solve the equation. (See...Ch. 1.6 - For Exercises 520, solve the equation. (See...Ch. 1.6 - For Exercises 5–20, solve the equation. (See...Ch. 1.6 - For Exercises 520, solve the equation. (See...Ch. 1.6 - For Exercises 520, solve the equation. (See...Ch. 1.6 - Prob. 10PECh. 1.6 - For Exercises 5–20, solve the equation. (See...Ch. 1.6 - For Exercises 5–20, solve the equation. (See...Ch. 1.6 - For Exercises 5–20, solve the equation. (See...Ch. 1.6 - Prob. 14PECh. 1.6 - For Exercises 520, solve the equation. (See...Ch. 1.6 - Prob. 16PECh. 1.6 - For Exercises 520, solve the equation. (See...Ch. 1.6 - Prob. 18PECh. 1.6 - For Exercises 5–20, solve the equation. (See...Ch. 1.6 - For Exercises 520, solve the equation. (See...Ch. 1.6 - For Exercises 21–28, solve the equation. (See...Ch. 1.6 - Prob. 22PECh. 1.6 - For Exercises 2128, solve the equation. (See...Ch. 1.6 - Prob. 24PECh. 1.6 - For Exercises 21–28, solve the equation. (See...Ch. 1.6 - Prob. 26PECh. 1.6 - For Exercises 21–28, solve the equation. (See...Ch. 1.6 - For Exercises 21–28, solve the equation. (See...Ch. 1.6 - Prob. 29PECh. 1.6 - A plane travels 800 mi from Dallas, Texas, to...Ch. 1.6 - Jean runs 6 mi and then rides 24 mi on her bicycle...Ch. 1.6 - Prob. 32PECh. 1.6 - For Exercises 3354, solve the equations. (See...Ch. 1.6 - For Exercises 3354, solve the equations. (See...Ch. 1.6 - For Exercises 3354, solve the equations. (See...Ch. 1.6 - Prob. 36PECh. 1.6 - For Exercises 3354, solve the equations. (See...Ch. 1.6 - Prob. 38PECh. 1.6 - For Exercises 3354, solve the equations. (See...Ch. 1.6 - Prob. 40PECh. 1.6 - For Exercises 33–54, solve the equations. (See...Ch. 1.6 - Prob. 42PECh. 1.6 - For Exercises 33–54, solve the equations. (See...Ch. 1.6 - Prob. 44PECh. 1.6 - For Exercises 33–54, solve the equations. (See...Ch. 1.6 - Prob. 46PECh. 1.6 - Prob. 47PECh. 1.6 - Prob. 48PECh. 1.6 - Prob. 49PECh. 1.6 - Prob. 50PECh. 1.6 - Prob. 51PECh. 1.6 - Prob. 52PECh. 1.6 - Prob. 53PECh. 1.6 - Prob. 54PECh. 1.6 - For Exercises 55–80, solve the equation. (See...Ch. 1.6 - Prob. 56PECh. 1.6 - Prob. 57PECh. 1.6 - Prob. 58PECh. 1.6 - For Exercises 5580, solve the equation. (See...Ch. 1.6 - Prob. 60PECh. 1.6 - For Exercises 5580, solve the equation. (See...Ch. 1.6 - Prob. 62PECh. 1.6 - For Exercises 55–80, solve the equation. (See...Ch. 1.6 - Prob. 64PECh. 1.6 - For Exercises 55–80, solve the equation. (See...Ch. 1.6 - Prob. 66PECh. 1.6 - Prob. 67PECh. 1.6 - Prob. 68PECh. 1.6 - Prob. 69PECh. 1.6 - Prob. 70PECh. 1.6 - For Exercises 55–80, solve the equation. (See...Ch. 1.6 - Prob. 72PECh. 1.6 - Prob. 73PECh. 1.6 - Prob. 74PECh. 1.6 - Prob. 75PECh. 1.6 - For Exercises 5580, solve the equation. (See...Ch. 1.6 - For Exercises 5580, solve the equation. (See...Ch. 1.6 - Prob. 78PECh. 1.6 - Prob. 79PECh. 1.6 - Prob. 80PECh. 1.6 - For Exercises 81–106, make an appropriate...Ch. 1.6 - For Exercises 81–106, make an appropriate...Ch. 1.6 - For Exercises 81–106, make an appropriate...Ch. 1.6 - Prob. 84PECh. 1.6 - For Exercises 81106, make an appropriate...Ch. 1.6 - Prob. 86PECh. 1.6 - For Exercises 81–106, make an appropriate...Ch. 1.6 - Prob. 88PECh. 1.6 - Prob. 89PECh. 1.6 - Prob. 90PECh. 1.6 - Prob. 91PECh. 1.6 - Prob. 92PECh. 1.6 - Prob. 93PECh. 1.6 - Prob. 94PECh. 1.6 - Prob. 95PECh. 1.6 - Prob. 96PECh. 1.6 - Prob. 97PECh. 1.6 - Prob. 98PECh. 1.6 - For Exercises 81–106, make an appropriate...Ch. 1.6 - Prob. 100PECh. 1.6 - Prob. 101PECh. 1.6 - Prob. 102PECh. 1.6 - Prob. 103PECh. 1.6 - Prob. 104PECh. 1.6 - Prob. 105PECh. 1.6 - Prob. 106PECh. 1.6 - For Exercises 107–118, solve for the indicated...Ch. 1.6 - Prob. 108PECh. 1.6 - Prob. 109PECh. 1.6 - Prob. 110PECh. 1.6 - For Exercises 107–118, solve for the indicated...Ch. 1.6 - Prob. 112PECh. 1.6 - Prob. 113PECh. 1.6 - Prob. 114PECh. 1.6 - Prob. 115PECh. 1.6 - Prob. 116PECh. 1.6 - For Exercises 107–118, solve for the indicated...Ch. 1.6 - Prob. 118PECh. 1.6 - Prob. 119PECh. 1.6 - Prob. 120PECh. 1.6 - Prob. 121PECh. 1.6 - For Exercises 121–122, solve the equation. 122. Ch. 1.6 - Prob. 123PECh. 1.6 - The distance d (in miles) that an observer can see...Ch. 1.6 - The percentage of drug released in the bloodstream...Ch. 1.6 - Prob. 126PECh. 1.6 - Prob. 127PECh. 1.6 - Prob. 128PECh. 1.6 - Prob. 129PECh. 1.6 - Prob. 130PECh. 1.6 - Prob. 131PECh. 1.6 - Prob. 132PECh. 1.6 - Joan and Henry both work for a mail-order company...Ch. 1.6 - Prob. 134PECh. 1.6 - Prob. 135PECh. 1.6 - Debbie is in a boat in the ocean 48 mi from point...Ch. 1.7 - Skill Practice 1 Solve the inequality. Graph the...Ch. 1.7 - Prob. 2SPCh. 1.7 - Skill Practice 3 Solve. 14y1or3+y5Ch. 1.7 - Prob. 4SPCh. 1.7 - Prob. 5SPCh. 1.7 - Prob. 6SPCh. 1.7 - Prob. 7SPCh. 1.7 - Prob. 8SPCh. 1.7 - Prob. 9SPCh. 1.7 - Prob. 10SPCh. 1.7 - Prob. 1PECh. 1.7 - Prob. 2PECh. 1.7 - Prob. 3PECh. 1.7 - Prob. 4PECh. 1.7 - Prob. 5PECh. 1.7 - Prob. 6PECh. 1.7 - Prob. 7PECh. 1.7 - Prob. 8PECh. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 9-26, solve the inequality. Graph...Ch. 1.7 - For Exercises 27-34, solve the compound...Ch. 1.7 - For Exercises 27-34, solve the compound...Ch. 1.7 - For Exercises 27-34, solve the compound...Ch. 1.7 - For Exercises 27-34, solve the compound...Ch. 1.7 - For Exercises 27-34, solve the compound...Ch. 1.7 - For Exercises 27-34, solve the compound...Ch. 1.7 - For Exercises 27-34, solve the compound...Ch. 1.7 - For Exercises 27-34, solve the compound...Ch. 1.7 - Write 2.8y15 as two separate inequalities joined...Ch. 1.7 - Write 12z2.4 as two separate inequalities joined...Ch. 1.7 - For Exercises 37-42, solve the compound...Ch. 1.7 - For Exercises 37-42, solve the compound...Ch. 1.7 - For Exercises 37-42, solve the compound...Ch. 1.7 - For Exercises 37-42, solve the compound...Ch. 1.7 - For Exercises 37-42, solve the compound...Ch. 1.7 - Prob. 42PECh. 1.7 - Prob. 43PECh. 1.7 - Prob. 44PECh. 1.7 - Prob. 45PECh. 1.7 - Prob. 46PECh. 1.7 - For Exercises 47-60, solve the inequality, and...Ch. 1.7 - For Exercises 47-60, solve the inequality, and...Ch. 1.7 - For Exercises 47-60, solve the inequality, and...Ch. 1.7 - For Exercises 47-60, solve the inequality, and...Ch. 1.7 - For Exercises 47-60, solve the inequality, and...Ch. 1.7 - For Exercises 47-60, solve the inequality, and...Ch. 1.7 - For Exercises 47-60, solve the inequality, and...Ch. 1.7 - For Exercises 47-60, solve the inequality, and...Ch. 1.7 - Prob. 55PECh. 1.7 - Prob. 56PECh. 1.7 - Prob. 57PECh. 1.7 - For Exercises 47-60, solve the inequality, and...Ch. 1.7 - Prob. 59PECh. 1.7 - Prob. 60PECh. 1.7 - Prob. 61PECh. 1.7 - Prob. 62PECh. 1.7 - Prob. 63PECh. 1.7 - Prob. 64PECh. 1.7 - Prob. 65PECh. 1.7 - Prob. 66PECh. 1.7 - Prob. 67PECh. 1.7 - Prob. 68PECh. 1.7 - Prob. 69PECh. 1.7 - Prob. 70PECh. 1.7 - Prob. 71PECh. 1.7 - Prob. 72PECh. 1.7 - Prob. 73PECh. 1.7 - Prob. 74PECh. 1.7 - Prob. 75PECh. 1.7 - Prob. 76PECh. 1.7 - Prob. 77PECh. 1.7 - Prob. 78PECh. 1.7 - Prob. 79PECh. 1.7 - The lengths of the sides of a triangle are given...Ch. 1.7 - Prob. 81PECh. 1.7 - Prob. 82PECh. 1.7 - Prob. 83PECh. 1.7 - Prob. 84PECh. 1.7 - Prob. 85PECh. 1.7 - Prob. 86PECh. 1.7 - Prob. 87PECh. 1.7 - Prob. 88PECh. 1.7 - Prob. 89PECh. 1.7 - Prob. 90PECh. 1.7 - Prob. 91PECh. 1.7 - Prob. 92PECh. 1.7 - Prob. 93PECh. 1.7 - Prob. 94PECh. 1.7 - Prob. 95PECh. 1.7 - Prob. 96PECh. 1.7 - Prob. 97PECh. 1.7 - Prob. 98PECh. 1.7 - Prob. 99PECh. 1.7 - Prob. 100PECh. 1.7 - Prob. 101PECh. 1.7 - Prob. 102PECh. 1.7 - Prob. 103PECh. 1.7 - Prob. 104PECh. 1.7 - Prob. 105PECh. 1.7 - Prob. 106PECh. 1.7 - Prob. 107PECh. 1.7 - Prob. 108PECh. 1.7 - Prob. 109PECh. 1.7 - Explain why x2=4 is equivalent to the equation...Ch. 1.7 - Prob. 111PECh. 1.7 - Prob. 112PECh. 1.7 - Prob. 113PECh. 1.7 - Prob. 114PECh. 1.7 - Prob. 115PECh. 1.7 - Prob. 116PECh. 1.7 - Solve the inequality for p:|pp|zpqn. (Do not...Ch. 1.7 - Prob. 118PECh. 1.7 - Prob. 1PRECh. 1.7 - Prob. 2PRECh. 1.7 - Prob. 3PRECh. 1.7 - Prob. 4PRECh. 1.7 - Prob. 5PRECh. 1.7 - Prob. 6PRECh. 1.7 - Prob. 7PRECh. 1.7 - Prob. 8PRECh. 1.7 - Prob. 9PRECh. 1.7 - Prob. 10PRECh. 1.7 - Prob. 11PRECh. 1.7 - Prob. 12PRECh. 1.7 - For Exercises 1-20, a. Identify the type of...Ch. 1.7 - Prob. 14PRECh. 1.7 - Prob. 15PRECh. 1.7 - For Exercises 1-20, a. Identify the type of...Ch. 1.7 - Prob. 17PRECh. 1.7 - Prob. 18PRECh. 1.7 - Prob. 19PRECh. 1.7 - Prob. 20PRECh. 1 - In Calculus you will see the symbol y . For...Ch. 1 - Prob. 2EICCh. 1 - Prob. 3EICCh. 1 - Prob. 4EICCh. 1 - Prob. 5EICCh. 1 - Prob. 6EICCh. 1 - Prob. 7EICCh. 1 - Prob. 8EICCh. 1 - Prob. 9EICCh. 1 - For Exercises 8-10, a. Simplify the expression. Do...Ch. 1 - Prob. 11EICCh. 1 - Prob. 12EICCh. 1 - Prob. 13EICCh. 1 - 14. A water trough has a cross section in the...Ch. 1 - Prob. 15EICCh. 1 - 1. Determine the restrictions on x for the...Ch. 1 - For Exercises 2-9, solve the equation. 2. Ch. 1 - For Exercises 2-9, solve the equation. 3. Ch. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Cassandra bought a 10-yr Treasury note that paid...Ch. 1 - Prob. 16RECh. 1 - Suppose that 250 ft3 of dry concrete mixture is...Ch. 1 - When Kevin commuted to work one morning, his...Ch. 1 - Prob. 19RECh. 1 - Monique plans to join a gym so that she can use...Ch. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - One pump can drain a pond in 22 hr. Working with a...Ch. 1 - Prob. 24RECh. 1 - Prob. 25RECh. 1 - For Exercises 26-28, write each expression in...Ch. 1 - Prob. 27RECh. 1 - For Exercises 26-28, write each expression in...Ch. 1 - Prob. 29RECh. 1 - 30. Simplify the powers of...Ch. 1 - Prob. 31RECh. 1 - For Exercises 31-40, perform the indicated...Ch. 1 - Prob. 33RECh. 1 - For Exercises 31-40, perform the indicated...Ch. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - For Exercises 41-46, solve the equation. 3y24y=86yCh. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - For Exercises 41-46, solve the equation. 44. Ch. 1 - For Exercises 41-46, solve the equation....Ch. 1 - Prob. 46RECh. 1 - For Exercises 47-48, determine the value of n that...Ch. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - For Exercises 51-52, answer true or false. 52. The...Ch. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - A television has a 50-in. diagonal screen. If the...Ch. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - Prob. 64RECh. 1 - For Exercises 65-82, solve the equation....Ch. 1 - For Exercises 65-82, solve the equation. 66. Ch. 1 - For Exercises 65-82, solve the equation. 67. Ch. 1 - For Exercises 65-82, solve the equation. 68. Ch. 1 - For Exercises 65-82, solve the equation....Ch. 1 - Prob. 70RECh. 1 - Prob. 71RECh. 1 - For Exercises 65-82, solve the equation. 72. Ch. 1 - Prob. 73RECh. 1 - Prob. 74RECh. 1 - For Exercises 65-82, solve the equation. 75. Ch. 1 - For Exercises 65-82, solve the equation. |6w|+7=2Ch. 1 - Prob. 77RECh. 1 - Prob. 78RECh. 1 - Prob. 79RECh. 1 - Prob. 80RECh. 1 - Prob. 81RECh. 1 - Prob. 82RECh. 1 - Prob. 83RECh. 1 - Prob. 84RECh. 1 - Prob. 85RECh. 1 - For Exercises 86-89, solve the inequality. Graph...Ch. 1 - For Exercises 86-89, solve the inequality. Graph...Ch. 1 - Prob. 88RECh. 1 - Prob. 89RECh. 1 - Prob. 90RECh. 1 - Prob. 91RECh. 1 - Prob. 92RECh. 1 - For Exercises 92-95, solve the compound...Ch. 1 - Prob. 94RECh. 1 - Prob. 95RECh. 1 - Prob. 96RECh. 1 - Prob. 97RECh. 1 - Prob. 98RECh. 1 - Prob. 99RECh. 1 - Prob. 100RECh. 1 - For Exercises 99-105, solve the equation or...Ch. 1 - For Exercises 99-105, solve the equation or...Ch. 1 - Prob. 103RECh. 1 - Prob. 104RECh. 1 - For Exercises 99-105, solve the equation or...Ch. 1 - Prob. 106RECh. 1 - Prob. 107RECh. 1 - Prob. 1TCh. 1 - 2. Simplify the powers of...Ch. 1 - Prob. 3TCh. 1 - Prob. 4TCh. 1 - Prob. 5TCh. 1 - Prob. 6TCh. 1 - Prob. 7TCh. 1 - Prob. 8TCh. 1 - For Exercises 9-24, solve the equation. 2d=1d+7Ch. 1 - Prob. 10TCh. 1 - Prob. 11TCh. 1 - Prob. 12TCh. 1 - For Exercises 9-24, solve the equation. (3x4)22=11Ch. 1 - Prob. 14TCh. 1 - For Exercises 9-24, solve the equation....Ch. 1 - Prob. 16TCh. 1 - Prob. 17TCh. 1 - For Exercises 9-24, solve the equation....Ch. 1 - For Exercises 9-24, solve the equation. 19. Ch. 1 - Prob. 20TCh. 1 - Prob. 21TCh. 1 - Prob. 22TCh. 1 - For Exercises 9-24, solve the equation. 2=|x3|6Ch. 1 - For Exercises 81106, make an appropriate...Ch. 1 - For Exercises 25-28, solve for the indicated...Ch. 1 - Prob. 26TCh. 1 - Prob. 27TCh. 1 - For Exercises 25-28, solve for the indicated...Ch. 1 - For Exercises 29-31, solve the compound...Ch. 1 - Prob. 30TCh. 1 - Prob. 31TCh. 1 - For Exercises 32-35, solve the equations and...Ch. 1 - Prob. 33TCh. 1 - Prob. 34TCh. 1 - Prob. 35TCh. 1 - Prob. 36TCh. 1 - 37. Two passengers leave the airport at Denver,...Ch. 1 - Prob. 38TCh. 1 - Prob. 39TCh. 1 - Prob. 40TCh. 1 - A varsity soccer player kicks a soccer ball...Ch. 1 - Prob. 42TCh. 1 - The equation r=3Vh gives the radius r of a right...Ch. 1 - For Exercises 1-7, perform the indicated...Ch. 1 - For Exercises 1-7, perform the indicated...Ch. 1 - For Exercises 1-7, perform the indicated...Ch. 1 - For Exercises 1-7, perform the indicated...Ch. 1 - For Exercises 1-7, perform the indicated...Ch. 1 - For Exercises 1-7, perform the indicated...Ch. 1 - For Exercises 1-7, perform the indicated...Ch. 1 - a. Write an absolute value expression that...Ch. 1 - Prob. 9CRECh. 1 - Divide and write the answer in the form a+bi....Ch. 1 - 11. Stephan borrowed a total of $8000 in two...Ch. 1 - Prob. 12CRECh. 1 - Prob. 13CRECh. 1 - For Exercises 12-17, solve the equation....Ch. 1 - For Exercises 12-17, solve the equation. x+42=xCh. 1 - Prob. 16CRECh. 1 - Prob. 17CRECh. 1 - Prob. 18CRECh. 1 - Prob. 19CRECh. 1 - Prob. 20CRE
Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
SEE MORE TEXTBOOKS
UG/ linear equation in linear algebra; Author: The Gate Academy;https://www.youtube.com/watch?v=aN5ezoOXX5A;License: Standard YouTube License, CC-BY
System of Linear Equations-I; Author: IIT Roorkee July 2018;https://www.youtube.com/watch?v=HOXWRNuH3BE;License: Standard YouTube License, CC-BY