
Numerical Methods for Engineers
7th Edition
ISBN: 9780073397924
Author: Steven C. Chapra Dr., Raymond P. Canale
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 12, Problem 34P
Mechanical/Aerospace Engineering
Three blocks are connected by a weightless cord and rest on an inclined plane (Fig. P12.34a). Employing a procedure similar to the one used in the analysis of the falling parachutists in Example 9.11 yields the following set of simultaneous equations (free-body diagrams are shown in Fig. P12.34b):
100a+T=519.72
50a−T+R=216.55
20a−R=108.28
Solve for acceleration a and the tensions T and R in the two ropes.
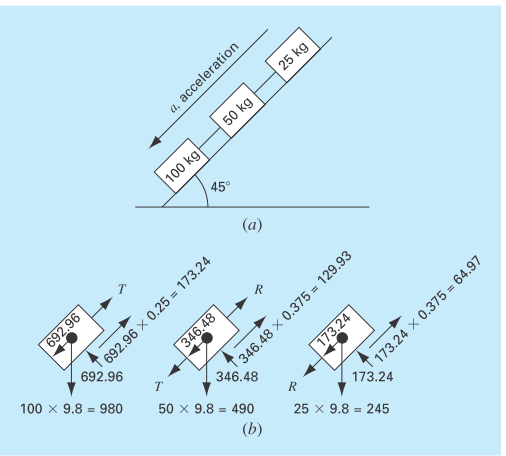
FIGURE P12.34
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Do College Students With Part-Time Jobs Sleep Less?
College students were surveyed about the number of hours they sleep each night.Group A = With part-time jobs | Group B = Without jobs
Group A: 6, 5, 7, 6, 5Group B: 8, 7, 9, 8, 7
Instructions:
State your hypothesis and perform a two-sample t-test with all formulas.
Create histograms for each group. Label axes and add titles.
Comment on the distribution shape (e.g., normal, skewed, etc.).Solve on pen and paper
This is advanced mathematics question that need detailed solutions
Question:
Let F be a field. Prove that F contains a unique smallest subfield, called the prime subfield, which is
isomorphic to either Q or Zp for some prime p.
Instructions:
•
Begin by identifying the identity element 1 € F.
•
Use the closure under addition and inverses to build a subring.
•
•
•
Show that either the map ZF or Q →F is an embedding.
Prove minimality and uniqueness.
Discuss the characteristic of a field and link it to the structure of the prime subfield.
Chapter 12 Solutions
Numerical Methods for Engineers
Ch. 12 - Chemical/Bio Engineering
12.1 Perform the same...Ch. 12 - Chemical/Bio Engineering If the input to reactor 3...Ch. 12 - Chemical/Bio Engineering Because the system shown...Ch. 12 - Chemical/Bio Engineering
12.4 Recompute the...Ch. 12 - Chemical/Bio Engineering Solve the same system as...Ch. 12 - Chemical/Bio Engineering
12.6 Figure P12.6 shows...Ch. 12 - Chemical/Bio Engineering
12.7 Employing the same...Ch. 12 - Chemical/Bio Engineering The Lower Colorado River...Ch. 12 - Chemical/Bio Engineering A stage extraction...Ch. 12 - Chemical/Bio Engineering
12.10 An irreversible,...
Ch. 12 - Chemical/Bio Engineering
12.11 A peristaltic pump...Ch. 12 - Chemical/Bio Engineering
12.12 Figure P12.12...Ch. 12 - Civil/Environmental Engineering A civil engineer...Ch. 12 - Civil/Environmental Engineering Perform the same...Ch. 12 - Civil/Environmental Engineering
12.15 Perform the...Ch. 12 - Civil/Environmental Engineering Calculate the...Ch. 12 - Civil/Environmental Engineering In the example for...Ch. 12 - Civil/Environmental Engineering Employing the same...Ch. 12 - Civil/Environmental Engineering Solve for the...Ch. 12 - Prob. 20PCh. 12 - Prob. 21PCh. 12 - Civil/Environmental Engineering
12.22 A truss is...Ch. 12 - Electrical Engineering
12.23 Perform the same...Ch. 12 - Electrical Engineering Perform the same...Ch. 12 - Electrical Engineering
12.25 Solve the circuit in...Ch. 12 - Electrical Engineering
12.26 An electrical...Ch. 12 - Electrical Engineering
12.27 Determine the...Ch. 12 - Electrical Engineering Determine the currents for...Ch. 12 - Electrical Engineering The following system of...Ch. 12 - Electrical Engineering
12.30 The following system...Ch. 12 - Mechanical/Aerospace Engineering Perform the same...Ch. 12 - Mechanical/Aerospace Engineering
12.32 Perform the...Ch. 12 - Mechanical/Aerospace Engineering
12.33 Idealized...Ch. 12 - Mechanical/Aerospace Engineering Three blocks are...Ch. 12 - Mechanical/Aerospace Engineering Perform a...Ch. 12 - Mechanical/Aerospace Engineering Perform the same...Ch. 12 - Mechanical/Aerospace Engineering
12.37 Consider...Ch. 12 - Mechanical/Aerospace Engineering The steady-state...Ch. 12 - Mechanical/Aerospace Engineering
12.40 A rod on a...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Topic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forward
- Complete solution requiredarrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forward
- Do on pen and paper onlyarrow_forwardProblem 9: The 30-kg pipe is supported at A by a system of five cords. Determine the force in each cord for equilibrium. B 60º A E Harrow_forwardd((x, y), (z, w)) = |xz|+|yw|, show that whether d is a metric on R² or not?. Q3/Let R be a set of real number and d: R² x R² → R such that -> d((x, y), (z, w)) = max{\x - zl, ly - w} show that whether d is a metric on R² or not?. Q4/Let X be a nonempty set and d₁, d₂: XXR are metrics on X let d3,d4, d5: XX → R such that d3(x, y) = 4d2(x, y) d4(x, y) = 3d₁(x, y) +2d2(x, y) d5(x,y) = 2d₁ (x,y))/ 1+ 2d₂(x, y). Show that whether d3, d4 and d5 are metric on X or not?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Matrix Factorization - Numberphile; Author: Numberphile;https://www.youtube.com/watch?v=wTUSz-HSaBg;License: Standard YouTube License, CC-BY