
Airline Revenue An airline has two classes of service: first class and coach. Management's experience has been that each aircraft should have at least 8 but no more than 16 first- class seats and at least 80 but no more than 120 coach seats
(a) If management decides that the ratio of first-class seats to coach seats should never exceed , with how many of each type of seat should an aircraft be configured to maximize revenue?
(b) If management decides that the ratio of first-class seats to coach seats should never exceed , with how many of each type of seat should an aircraft be configured to maximize revenue?
(c) If you were management, what would you do?
[Hint: Assume that the airline charges for a coach seat and for a first-class seat; .]
To solve: The given linear programming problem.
Answer to Problem 31AYU
Solution:
a. The revenue is maximized when the aircraft is configured with 10 First Class seats and 120 coach seats.
b. The revenue is maximized when the aircraft is configured with 15 First Class seats and 120 coach seats.
c. First Class Seats to Coach Seats does not exceed ratio.
Explanation of Solution
Given:
- Each aircraft should have at least 8 but not more than 16 first class seats.
- Each aircraft should have at least 80 by not more than 120 coach seats.
- is the charges for a coach seat and is the charges for First class seat such that and .
Calculation:
Begin by assigning symbols for the two variables.
be the number of First Class seats.
be the number of Coach seats.
If be the total revenue,
The goal is to maximize subject to certain constraints on . Because represents number of seats, the only meaningful values of are non-negative.
Therefore, .
Also from the given data we get,
a. If the ratio of first class to coach seats should not exceed , the following can be written or .
Therefore, the linear programming problem may be stated as,
Maximize, .
Subject to,
The graph of the constraints is illustrated in the figure below.
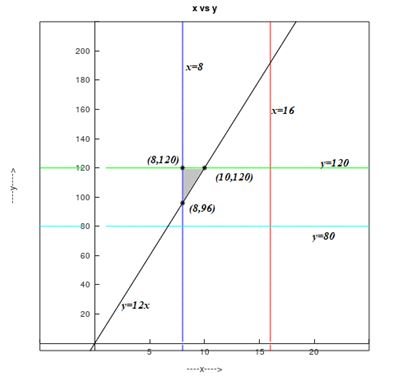
The corner points are as follows:
| Corner points are | Value of objective function
|
Since , the revenue is maximized when the aircraft is configured with 10 First Class seats and 120 coach seats.
b. If the ratio of first class to coach seats should not exceed , the following can be written or .
Therefore, the linear programming problem may be stated as,
Maximize, .
Subject to,
The graph of the constraints is illustrated in the figure below.
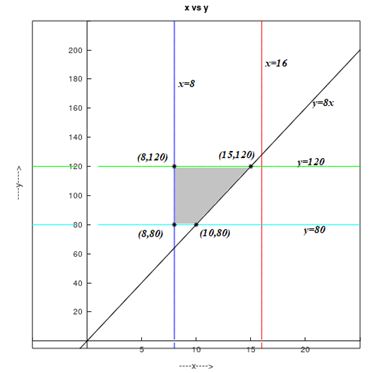
The corner points are as follows:
| Corner points are | Value of objective function
|
Since , the revenue is maximized when the aircraft is configured with 15 First Class seats and 120 coach seats.
c. If the ratio of first class seats to coach seats should not exceed , the total revenue is . If the ratio of first class seats to coach seats should not exceed , the total revenue is . Since , the revenue is maximized when First Class Seats to Coach Seats ration does not exceed ratio.
Chapter 11 Solutions
Precalculus
Additional Math Textbook Solutions
Precalculus: Mathematics for Calculus (Standalone Book)
Elementary Statistics (13th Edition)
Basic Business Statistics, Student Value Edition
College Algebra with Modeling & Visualization (5th Edition)
University Calculus: Early Transcendentals (4th Edition)
College Algebra (7th Edition)
- practice problem please help!arrow_forwardFind a parameterization for a circle of radius 4 with center (-4,-6,-3) in a plane parallel to the yz plane. Write your parameterization so the y component includes a positive cosine.arrow_forward~ exp(10). A 3. Claim number per policy is modelled by Poisson(A) with A sample x of N = 100 policies presents an average = 4 claims per policy. (i) Compute an a priory estimate of numbers of claims per policy. [2 Marks] (ii) Determine the posterior distribution of A. Give your argument. [5 Marks] (iii) Compute an a posteriori estimate of numbers of claims per policy. [3 Marks]arrow_forward
- 2. The size of a claim is modelled by F(a, λ) with a fixed a a maximum likelihood estimate of A given a sample x with a sample mean x = 11 = 121. Give [5 Marks]arrow_forwardRobbie Bearing Word Problems Angles name: Jocelyn date: 1/18 8K 2. A Delta airplane and an SouthWest airplane take off from an airport at the same time. The bearing from the airport to the Delta plane is 23° and the bearing to the SouthWest plane is 152°. Two hours later the Delta plane is 1,103 miles from the airport and the SouthWest plane is 1,156 miles from the airport. What is the distance between the two planes? What is the bearing from the Delta plane to the SouthWest plane? What is the bearing to the Delta plane from the SouthWest plane? Delta y SW Angles ThreeFourthsMe MATH 2arrow_forwardFind the derivative of the function. m(t) = -4t (6t7 - 1)6arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





