Calculus Early Transcendentals, Binder Ready Version
Calculus Early Transcendentals, Binder Ready Version
11th Edition
ISBN: 9781118883822
Author: Howard Anton, Irl C. Bivens, Stephen Davis
Publisher: WILEY
bartleby

Concept explainers

Vertices Of An Ellipse
In the study of the conic section of the geometry, An ellipse is a plane curve surrounding two focal points, or foci where the set of all locus of points in the plane has their sum of the distances to the two foci is constant. On the ellipse curve, it is…
bartleby

Videos

Textbook Question
Book Icon
Chapter 11.7, Problem 54ES

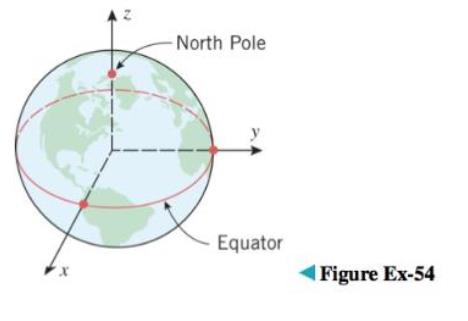
The Earth’s rotation causes a flattening at the poles, so its shape is often modeled as an oblate spheroid rather than a sphere (see Exercise 53 for terminology). One of the models used by global positioning satellites is the World Geodetic System of 1984 (WGS-84), which treats the Earth as an oblate spheroid whose equatorial radius is 6378.1370 km and whose polar radius (the distance from the Earth’s center to the poles) is 6356.5231 km. Use the WGS-84 model to find an equation for the surface of the Earth relative to the coordinate system shown in the ac-companying figure.

Chapter 11.7, Problem 54ES, The Earth’s rotation causes a flattening at the poles, so its shape is often modeled as an oblate

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 11.7, Problem 53ES
Next
Chapter 11.7, Problem 55ES
Students have asked these similar questions
I do not understand your writing, and can you explane it any more?
Write the equation of a sphere of radius 3 in all three coordinates--cartesian, cylindrical, and spherical.
What are the coordinates of the top point of an equilateral triangle if the corners of its base are on (0,0) and (100,0)?

Chapter 11 Solutions

Calculus Early Transcendentals, Binder Ready Version

Ch. 11.1 - The distance between the point 1,2,0and4,0,5is.Ch. 11.1 - The graph of x32+y22+z+12=16 is a of radius ...Ch. 11.1 - The shortest distance from the point (4, 0, 5) to...Ch. 11.1 - Let S be the graph of x2+z2+6z=16in3-space. (a)...Ch. 11.1 - In each part, find the coordinates of the eight...Ch. 11.1 - A cube of side 4 has its geometric center at the...Ch. 11.1 - Suppose that a box has its faces parallel to the...Ch. 11.1 - Suppose that a box has its faces paralled to the...Ch. 11.1 - Interpret the graph of x=1 in the contexts of (a)...Ch. 11.1 - Consider the points P(3, 1,0) and Q(1,4,4). (a)...
Ch. 11.1 - (a) Consider a box whose sides have lengths a,b,...Ch. 11.1 - (a) Make a conjecture about the set of points in...Ch. 11.1 - Find the center and radius of the sphere that has...Ch. 11.1 - Show that (4,5,2), (1,7,3), and (2, 4, 5) are...Ch. 11.1 - (a) Show that 2,1,6,4,7,9,and8,5,6 are the...Ch. 11.1 - Find the distance from the point 5,2,3 to the...Ch. 11.1 - In each part, find the standard equation of the...Ch. 11.1 - Find equation of two spheres that are centered at...Ch. 11.1 - In each part, find an equation of the sphere with...Ch. 11.1 - (a) Find an equation of the sphere that is...Ch. 11.1 - A sphere has center in the first octant and is...Ch. 11.1 - A sphere has center in the first octant and is...Ch. 11.1 - Determine whether the statement is true or false....Ch. 11.1 - Determine whether the statement is true or false....Ch. 11.1 - Determine whether the statement is true or false....Ch. 11.1 - Determine whether the statement is true or false....Ch. 11.1 - Describe the surface whose equation is given....Ch. 11.1 - Prob. 24ESCh. 11.1 - Describe the surface whose equation is given....Ch. 11.1 - Describe the surface whose equation is given....Ch. 11.1 - Describe the surface whose equation is given....Ch. 11.1 - Describe the surface whose equation is given....Ch. 11.1 - In each part, sketch the portion of the surface...Ch. 11.1 - In each part, sketch the graph of the equation in...Ch. 11.1 - In each part, sketch the graph of the equation in...Ch. 11.1 - In each part, sketch the graph of the equation in...Ch. 11.1 - In each part, write an equation for the surface....Ch. 11.1 - Find equation for the following right circular...Ch. 11.1 - Sketch the surface in 3-space. y=sinxCh. 11.1 - Sketch the surface in 3-space. y=exCh. 11.1 - Sketch the surface in 3-space. z=1y2Ch. 11.1 - Sketch the surface in 3-space. z=cosxCh. 11.1 - Sketch the surface in 3-space. 2x+z=3Ch. 11.1 - Sketch the surface in 3-space. 2x+3y=6Ch. 11.1 - Sketch the surface in 3-space. 4x2+9z2=36Ch. 11.1 - Sketch the surface in 3-space. z=3xCh. 11.1 - Sketch the surface in 3-space. y24z2=4Ch. 11.1 - Sketch the surface in 3-space. yz=1Ch. 11.1 - Generate the curve y=x3/1+x2 in the xy-plane using...Ch. 11.1 - Use a graphing utility to generate the curve...Ch. 11.1 - If a bug walks on the sphere x2+y2+z2+2x2y4z3=0...Ch. 11.1 - Describe the set of all points in 3-space whose...Ch. 11.1 - Describe the set of all points in 3-space whose...Ch. 11.1 - The distance between a point Px,y,z and the point...Ch. 11.1 - As shown in the accompanying figure, a bowling...Ch. 11.1 - Consider the equation x2+y2+z2+Gx+Hy+Iz+J=0 and...Ch. 11.1 - (a) The accompanying figure shows a surface of...Ch. 11.1 - In each part, use the idea in Exercise 53(a) to...Ch. 11.1 - Show that for all values of and, and the point...Ch. 11.1 - Explain how you might determine whether a set of...Ch. 11.1 - Discuss what happens geometrically when equations...Ch. 11.2 - Ifv=3,1,7andw=4,10,5,thenav=bv+w=cvw=d2v=Ch. 11.2 - Prob. 2QCECh. 11.2 - The unit vector in 2-space that makes an angle of...Ch. 11.2 - Consider points A3,4,0andB0,0,5. (a) AB= (b) If v...Ch. 11.2 - Prob. 1ESCh. 11.2 - Prob. 2ESCh. 11.2 - Prob. 3ESCh. 11.2 - Sketch the vector with their initial points at the...Ch. 11.2 - Prob. 5ESCh. 11.2 - Prob. 6ESCh. 11.2 - Find the component of the vector P1P2....Ch. 11.2 - Find the component of the vector P1P2....Ch. 11.2 - (a) Find the terminal point of v=3i2j if the...Ch. 11.2 - (a) Find the terminal point of v=7,6 if the...Ch. 11.2 - Perform the stated operations on the given vectors...Ch. 11.2 - Perform the stated operations on the given vectors...Ch. 11.2 - Find the norm of v....Ch. 11.2 - Prob. 14ESCh. 11.2 - Letu=i3j+2k,v=i+j,andw=2i+2j4k. Find...Ch. 11.2 - Is it possible to have uv=u+v if u and are nonzero...Ch. 11.2 - Determine whether the statement is true or false....Ch. 11.2 - Prob. 18ESCh. 11.2 - Determine whether the statement is true or false....Ch. 11.2 - Prob. 20ESCh. 11.2 - Prob. 21ESCh. 11.2 - Find unit vector that satisfy the stated...Ch. 11.2 - Find the vectors that satisfy the stated...Ch. 11.2 - Find the vectors that satisfy the stated...Ch. 11.2 - In each part, find the component form of the...Ch. 11.2 - Find the component forms of v+wandvw in 2-space,...Ch. 11.2 - Find the component form of v+w, given that v and w...Ch. 11.2 - Find the component form of v+w, given that v and w...Ch. 11.2 - In each part, sketch the vector u+v+w and express...Ch. 11.2 - In each pat of exercise 29, sketch the vector uv+w...Ch. 11.2 - Let u=1,3,v=2,1,w=4,1. Find the vector x that...Ch. 11.2 - Let u=1,1,v=0,1,w=3,4. Find the vector x that...Ch. 11.2 - Find u and v if u+2v=3ikand3uv=i+j+k.Ch. 11.2 - Find u and v if u+v=2,3and3u+2v=1,2.Ch. 11.2 - Use vector to find the lengths of the diagonals of...Ch. 11.2 - Use vector to find the fourth vertex of a...Ch. 11.2 - (a) Given that v=3, find all values of k such that...Ch. 11.2 - What do you know about k and v if kv=0?Ch. 11.2 - Prob. 39ESCh. 11.2 - In each part, find two unit vector in 3-space that...Ch. 11.2 - Let r=x,y be an arbitrary vector. In each part,...Ch. 11.2 - Let r=x,yandr0=x0,y0. In each part, describe the...Ch. 11.2 - Let r=x,y,z be an arbitrary vector. In each part,...Ch. 11.2 - Let r1=x1,y1,r2=x2,y2andr=x,y. Assuming that...Ch. 11.2 - Find the magnitude of the resultant force and the...Ch. 11.2 - Find the magnitude of the resultant force and the...Ch. 11.2 - Find the magnitude of the resultant force and the...Ch. 11.2 - Find the magnitude of the resultant force and the...Ch. 11.2 - Find the magnitude of the resultant force and the...Ch. 11.2 - Find the magnitude of the resultant force and the...Ch. 11.2 - Prob. 51ESCh. 11.2 - Prob. 52ESCh. 11.2 - The accompanying figure shows a 250 lb traffic...Ch. 11.2 - Find the tensions in the cables shown in the...Ch. 11.2 - Prob. 55ESCh. 11.2 - A block weighing 100 N is suspended by cables A...Ch. 11.2 - A vector w is said to be a liner combination of...Ch. 11.2 - A vector w is a linear combination of the vectors...Ch. 11.2 - Prob. 59ESCh. 11.2 - Prove parts (a), (c), and (e) of Theorem 11.2.6...Ch. 11.2 - Prove parts (d), (g), and (h) of Theorem 11.2.6...Ch. 11.2 - Prove part (f) of Theorem 11.2.6 geometrically.Ch. 11.2 - Use vectors to prove that the line segment joining...Ch. 11.2 - Use vectors to prove that the midpoints of the...Ch. 11.3 - 3,1,26,0,5=Ch. 11.3 - Suppose that u, v, and w are vector in 3-space...Ch. 11.3 - Prob. 3QCECh. 11.3 - The direction cosines of2,1,3arecos=,cos=,andcos=.Ch. 11.3 - Prob. 5QCECh. 11.3 - Prob. 1ESCh. 11.3 - Prob. 2ESCh. 11.3 - Prob. 3ESCh. 11.3 - Does the tringle in 3-space with vertices...Ch. 11.3 - The accompanying figure shows eight vector that...Ch. 11.3 - The accompanying figure shows six vector that are...Ch. 11.3 - (a) Use vectors to show that...Ch. 11.3 - Prob. 8ESCh. 11.3 - In each part, determine whether the given...Ch. 11.3 - The first, second, and third component of the...Ch. 11.3 - The i, j, and k component of the “race vector�...Ch. 11.3 - Let u=1,2,v=4,2,andw=6,0. find au7v+wbuwwcuvwduvw.Ch. 11.3 - Find r so that the vector from the point A1,1,3 to...Ch. 11.3 - Find two unit vector in 2-space that make an angle...Ch. 11.3 - Find the direction cosines of v and confirm that...Ch. 11.3 - Prob. 16ESCh. 11.3 - Show that the direction cosines of a vector...Ch. 11.3 - Let and be the angles shown in the accompanying...Ch. 11.3 - The accompanying figure shown a cube. (a) Find the...Ch. 11.3 - Show the two nonzero vectors v1andv2 are...Ch. 11.3 - Prob. 21ESCh. 11.3 - Find, to the nearest degree, the acute angle...Ch. 11.3 - Find, to the nearest degree, the angles that a...Ch. 11.3 - In each part, find the vector component of v along...Ch. 11.3 - Prob. 25ESCh. 11.3 - Express the vector v as the sum of a vector...Ch. 11.3 - Express the vector v as the sum of a vector...Ch. 11.3 - Determine whether the statement is true or false....Ch. 11.3 - Determine whether the statement is true or false....Ch. 11.3 - Determine whether the statement is true or false....Ch. 11.3 - Determine whether the statement is true or false....Ch. 11.3 - Prob. 32ESCh. 11.3 - Use the method of Exercise 32 to find the distance...Ch. 11.3 - Prob. 34ESCh. 11.3 - For the child in Exercise 34, estimate how much...Ch. 11.3 - Suppose that the slide in Exercise 34 is 4 m long....Ch. 11.3 - Prob. 37ESCh. 11.3 - Prob. 38ESCh. 11.3 - Prob. 39ESCh. 11.3 - Prob. 40ESCh. 11.3 - Let u and v be adjacent sides of a parallelogram....Ch. 11.3 - Let u and v be adjacent sides of a parallelogram....Ch. 11.3 - Prob. 43ESCh. 11.3 - Prob. 44ESCh. 11.3 - Show that if v1,v2,andv3 are mutually orthogonal...Ch. 11.3 - Show that the three vectors...Ch. 11.3 - For each x in ,+, be the vector from the origin to...Ch. 11.3 - Let u be a unit vector in the xy-plane of an...Ch. 11.3 - Prove parts (b) and (e) of Theorem 11.3.2 for...Ch. 11.3 - Discuss some for the similarities and differences...Ch. 11.4 - a3245=b321321555=Ch. 11.4 - 1,2,03,0,4=Ch. 11.4 - Suppose that u, v, and w are vectors in 3-space...Ch. 11.4 - Let u=i5k,v=2i4j+k,andw=3i2j+5k. auvw= (b) The...Ch. 11.4 - (a) Use a determinant to find the cross product...Ch. 11.4 - In each part, use the two methods in Exercise 1 to...Ch. 11.4 - Find uv and check that it is orthogonal to both u...Ch. 11.4 - Find uv and check that it is orthogonal to both u...Ch. 11.4 - Find uv and check that it is orthogonal to both u...Ch. 11.4 - Find uv and check that it is orthogonal to both u...Ch. 11.4 - Let u=2,1,3,v=0,1,7,andw=1,4,5. Find...Ch. 11.4 - Use a CAS or a calculating utility that can...Ch. 11.4 - Find the direction cosines of uv for the vectors u...Ch. 11.4 - Find two unit vectors that are orthogonal to both...Ch. 11.4 - Find two unit vectors that are normal to the plane...Ch. 11.4 - Find two unit vectors that are parallel to the...Ch. 11.4 - Determine whether the statement is true or false....Ch. 11.4 - Determine whether the statement is true or false....Ch. 11.4 - Determine whether the statement is true or false....Ch. 11.4 - Determine whether the statement is true or false....Ch. 11.4 - Find the area of the parallelogram that has u and...Ch. 11.4 - Find the area of the parallelogram that has u and...Ch. 11.4 - Find the area of the triangle with vertices P, Q,...Ch. 11.4 - Find the area of the triangle with vertices P, Q,...Ch. 11.4 - Finduvw. u=2i3j+k,v=4i+j3k,w=j+5kCh. 11.4 - Finduvw. u=1,2,2,v=0,3,2,w=4,1,3Ch. 11.4 - Prob. 23ESCh. 11.4 - Prob. 24ESCh. 11.4 - Use a scalar triple product to find the volume of...Ch. 11.4 - Use a scalar triple product to find the volume of...Ch. 11.4 - In each part, use a scalar triple product to...Ch. 11.4 - Suppose that uvw=3. Find auwvbvwucwuvdvuweuwvfvww.Ch. 11.4 - Consider the parallelepiped with adjacent edges...Ch. 11.4 - Show that in 3-space the distance d from a point P...Ch. 11.4 - Use the result in Exercise 30 to find the distance...Ch. 11.4 - It is a theorem of solid geometry that the volume...Ch. 11.4 - Use the result of Exercise 32 to find the volume...Ch. 11.4 - Prob. 34ESCh. 11.4 - Let A, B, C, and D be four distinct points in...Ch. 11.4 - Let A, B, and C be three distinct noncollinear...Ch. 11.4 - Prob. 37ESCh. 11.4 - Prob. 38ESCh. 11.4 - The accompanying figure shows a force F of 10 lb...Ch. 11.4 - Prob. 40ESCh. 11.4 - As shown in the accompanying figure, a force of...Ch. 11.4 - Prove parts (b) and (c) of Theorem 11.4.3.Ch. 11.4 - Prove parts (d) and (e) of Theorem 11.4.3.Ch. 11.4 - Prove part (b) of Theorem 11.4.1 for 33...Ch. 11.4 - Expressions of the form uvwanduvw are called...Ch. 11.4 - (a) Use the result in Exercise 45 to show that uvw...Ch. 11.4 - In each part, use the result in Exercise 45 to...Ch. 11.4 - Prove: If a, b, c, and d lie in the same plane...Ch. 11.4 - Use a CAS to approximate the minimum area of a...Ch. 11.4 - If a force F is applied to an object at a point Q,...Ch. 11.4 - Discuss some of the similarities and differences...Ch. 11.5 - Prob. 1QCECh. 11.5 - Parametric equation for the line through (5 3 7)...Ch. 11.5 - Parametric equation for the line segment joining...Ch. 11.5 - The line through the points 3,8,4and1,0,8...Ch. 11.5 - (a) Find parametric equations for the lines...Ch. 11.5 - (a) Find parametric equations for the line...Ch. 11.5 - Find parametric equations for the line through...Ch. 11.5 - Find parametric equations for the line through...Ch. 11.5 - Find parametric equations for the line whose...Ch. 11.5 - Find parametric equations for the line whose...Ch. 11.5 - Find a point P on the line and a vector v parallel...Ch. 11.5 - Find a point P on the line and a vector v parallel...Ch. 11.5 - Express the given parametric equations of a line...Ch. 11.5 - Express the given parametric equations of a line...Ch. 11.5 - Determine whether the statement is true or false....Ch. 11.5 - Determine whether the statement is true or false....Ch. 11.5 - Determine whether the statement is true or false....Ch. 11.5 - Determine whether the statement is true or false....Ch. 11.5 - Find parametric equations of the line that...Ch. 11.5 - Find parametric equations of the line that...Ch. 11.5 - Find parametric equations of the line that...Ch. 11.5 - Find parametric equations of the line that...Ch. 11.5 - Find parametric equations of the line that...Ch. 11.5 - Find parametric equations of the line that...Ch. 11.5 - Find parametric equations of the line that...Ch. 11.5 - Find parametric equations of the line that...Ch. 11.5 - Where does the line x=1+3t,y=2t intersect...Ch. 11.5 - Where does the line x,y=4t,3t intersect the circle...Ch. 11.5 - Find the intersections of the lines with the...Ch. 11.5 - Find the intersections of the lines with the...Ch. 11.5 - Where does the line x=1+t,y=3t,z=2t intersect the...Ch. 11.5 - Where does the line x=2t,y=3t,z=1+2t intersect the...Ch. 11.5 - Show that the lines L1andL2 intersect, and find...Ch. 11.5 - Show that the lines L1andL2 intersect, and find...Ch. 11.5 - Show that the lines L1andL2 are skew....Ch. 11.5 - Show that the lines L1andL2 are skew....Ch. 11.5 - Determine whether the lines L1andL2 are parallel....Ch. 11.5 - Determine whether the lines L1andL2 are parallel....Ch. 11.5 - Determine whether the points P1,P2,andP3 lie on...Ch. 11.5 - Determine whether the points P1,P2,andP3 lie on...Ch. 11.5 - Show that the lines L1andL2 are the same....Ch. 11.5 - Show that the lines L1andL2 are the same....Ch. 11.5 - Prob. 39ESCh. 11.5 - Prob. 40ESCh. 11.5 - Sketch the vectors r0=2,0andr1=1,3, and then...Ch. 11.5 - Sketch the vectors r0=2,0,4andr1=0,4,0, and then...Ch. 11.5 - Describe the line segment represented by the...Ch. 11.5 - Describe the line segment represented by the...Ch. 11.5 - Find the point on the line segment joining...Ch. 11.5 - Find the point on the line segment joining...Ch. 11.5 - Use the method in Exercise 32 of Section 11.3 to...Ch. 11.5 - Use the method in Exercise 32 of Section 11.3 to...Ch. 11.5 - Show that the lines L1andL2 are parallel, and find...Ch. 11.5 - Show that the lines L1andL2 are parallel, and find...Ch. 11.5 - (a) Find parametric equations for the line through...Ch. 11.5 - Let L be the line that passes through the point...Ch. 11.5 - (a) Describe the line whose symmetric equations...Ch. 11.5 - Consider the lines L1andL2 whose symmetric...Ch. 11.5 - Let L1andL2 be the lines whose parametric...Ch. 11.5 - Let L1andL2 be the lines whose parametric...Ch. 11.5 - Find parametric equations of the line that...Ch. 11.5 - Find parametric equations of the line that...Ch. 11.5 - Two bugs are walking along lines in 3-space. At...Ch. 11.5 - Suppose that the temperature Tat a point x,y,z on...Ch. 11.6 - The point-normal form of the equation of the plane...Ch. 11.6 - A normal vector for the plane 4x2y+7z11=0is.Ch. 11.6 - A normal vector for the plane through the point...Ch. 11.6 - The acute angle of intersection of the planes...Ch. 11.6 - The distance between the point (9,8,3) and the...Ch. 11.6 - Find equation of the planes P1,P2,andP3 that are...Ch. 11.6 - Find equation of the planes P1,P2,andP3 that are...Ch. 11.6 - Find an equation of the plane that passes through...Ch. 11.6 - Find an equation of the plane that passes through...Ch. 11.6 - Find an equation of the plane that passes through...Ch. 11.6 - Find an equation of the plane that passes through...Ch. 11.6 - Find an equation of the plane indicated in the...Ch. 11.6 - Find an equation of the plane indicated in the...Ch. 11.6 - Find an equation of the plane indicated in the...Ch. 11.6 - Find an equation of the plane indicated in the...Ch. 11.6 - Find an equation of the plane that passes through...Ch. 11.6 - Find an equation of the plane that passes through...Ch. 11.6 - Determine whether the planes are parallel,...Ch. 11.6 - Determine whether the planes are parallel,...Ch. 11.6 - Determine whether the line and plane are parallel,...Ch. 11.6 - Determine whether the line and plane are parallel,...Ch. 11.6 - Determine whether the line and plane intersect; if...Ch. 11.6 - Determine whether the line and plane intersect; if...Ch. 11.6 - Find the acute angle of intersection of the planes...Ch. 11.6 - Find the acute angle of intersection of the planes...Ch. 11.6 - Determine whether the statement is true or false....Ch. 11.6 - Prob. 22ESCh. 11.6 - True-False Determine whether the statement is true...Ch. 11.6 - True-False Determine whether the statement is true...Ch. 11.6 - Find an equation of the plane that satisfies the...Ch. 11.6 - Find the equation of the plane that satisfies the...Ch. 11.6 - Find the equation of the plane that satisfies the...Ch. 11.6 - Find the equation of the plane that satisfies the...Ch. 11.6 - Find the equation of the plane that satisfies the...Ch. 11.6 - Find the equation of the plane that satisfies the...Ch. 11.6 - Find the equation of the plane that satisfies the...Ch. 11.6 - Find the equation of the plane that satisfies the...Ch. 11.6 - Find the equation of the plane that satisfies the...Ch. 11.6 - Find the equation of the plane that satisfies the...Ch. 11.6 - Find parametric equation of the line through the...Ch. 11.6 - Let L be the line x=3t+1,y=5t,z=t. (a) Show that L...Ch. 11.6 - Prob. 37ESCh. 11.6 - Show that the lines...Ch. 11.6 - Do the points 1,0,1,0,2,3,2,1,1, and 4,2,3 lie in...Ch. 11.6 - Show that if a, b, and c, are nonzero, then the...Ch. 11.6 - Find the parametric equation of the line of...Ch. 11.6 - Find the parametric equation of the line of...Ch. 11.6 - Find the distance between the point and the plane....Ch. 11.6 - Find the distance between the point and the plane....Ch. 11.6 - Find the distance between the given parallel...Ch. 11.6 - Find the distance between the given parallel...Ch. 11.6 - Prob. 47ESCh. 11.6 - Prob. 48ESCh. 11.6 - Find an equation of the sphere with center 2,1,3...Ch. 11.6 - Locate the point of intersection of the plane...Ch. 11.6 - Show that the line x=1+t,y=3+2t,z=t and the plane...Ch. 11.6 - Formulas (1), (2), (3), (5), and (10), which apply...Ch. 11.6 - (a) Show the distance D between parallel planes...Ch. 11.7 - For the surface 4x2+y2+z2=9, classify the...Ch. 11.7 - For the surface 4x2+z2y2=9, classify the indicated...Ch. 11.7 - For the surface 4x2+y2z=0, classify the indicated...Ch. 11.7 - Classify each surface as an ellipsoid, hyperboloid...Ch. 11.7 - Identify the quadric surface as an ellipsoid,...Ch. 11.7 - Identify the quadric surface as an ellipsoid,...Ch. 11.7 - Find the equation for and sketch the surface that...Ch. 11.7 - Find an equation for and sketch the surface that...Ch. 11.7 - The given equation represent quadric surfaces...Ch. 11.7 - For each of the surfaces in Exercise 5, find the...Ch. 11.7 - Prob. 7ESCh. 11.7 - Prob. 8ESCh. 11.7 - In these exercises, traces of the surfaces in the...Ch. 11.7 - In these exercises, traces of the surfaces in the...Ch. 11.7 - Determine whether the statement is true or false....Ch. 11.7 - Determine whether the statement is true or false....Ch. 11.7 - Determine whether the statement is true or false....Ch. 11.7 - Determine whether the statement is true or false....Ch. 11.7 - Identify and sketch the quadric surface....Ch. 11.7 - Identify and sketch the quadric surface....Ch. 11.7 - Identify and sketch the quadric surface....Ch. 11.7 - Identify and sketch the quadric surface. x2+y2z2=9Ch. 11.7 - Identify and sketch the quadric surface....Ch. 11.7 - Prob. 20ESCh. 11.7 - Identify and sketch the quadric surface....Ch. 11.7 - Identify and sketch the quadric surface....Ch. 11.7 - Identify and sketch the quadric surface. z=y2x2Ch. 11.7 - Identify and sketch the quadric surface. 16z=y2x2Ch. 11.7 - Identify and sketch the quadric surface. 4z=x2+2y2Ch. 11.7 - Identify and sketch the quadric surface. z3x23y2=0Ch. 11.7 - The given equation represents a quadric surface...Ch. 11.7 - The given equation represents a quadric surface...Ch. 11.7 - The given equation represents a quadric surface...Ch. 11.7 - The given equation represents a quadric surface...Ch. 11.7 - The given equation represents a quadric surface...Ch. 11.7 - The given equation represents a quadric surface...Ch. 11.7 - Sketch the surface. z=x2+y2Ch. 11.7 - Sketch the surface. z=1x2y2Ch. 11.7 - Sketch the surface. z=x2+y21Ch. 11.7 - Sketch the surface. z=1+x2+y2Ch. 11.7 - Identify the surface and make a rough sketch that...Ch. 11.7 - Identify the surface and make a rough sketch that...Ch. 11.7 - Identify the surface and make a rough sketch that...Ch. 11.7 - Identify the surface and make a rough sketch that...Ch. 11.7 - Use the ellipsoid 4x2+9y2+18z2=72 in in these...Ch. 11.7 - Use the ellipsoid 4x2+9y2+18z2=72 in in these...Ch. 11.7 - These exercises refer to the hyperbolic paraboloid...Ch. 11.7 - These exercises refer to the hyperbolic paraboloid...Ch. 11.7 - These exercises refer to the hyperbolic paraboloid...Ch. 11.7 - These exercises refer to the hyperbolic paraboloid...Ch. 11.7 - Sketch the region enclosed between the surfaces...Ch. 11.7 - Sketch the region enclosed between the surfaces...Ch. 11.7 - Find an equation for the surface generation by...Ch. 11.7 - Find an equation for the surface generation by...Ch. 11.7 - Find an equation of the surface consisting of all...Ch. 11.7 - Find an equation of the surface consisting of all...Ch. 11.7 - If a sphere x2a2+y2a2+z2a2=1 of radius a is...Ch. 11.7 - The Earth’s rotation causes a flattening at the...Ch. 11.7 - Use the method of slicing to show that the volume...Ch. 11.7 - Discuss some of the connections between conic...Ch. 11.7 - Give a sequence of steps for determining the type...Ch. 11.8 - The conversion formula from cylindrical...Ch. 11.8 - The conversion formulas from spherical coordinates...Ch. 11.8 - The conversion formulas from spherical coordinates...Ch. 11.8 - Prob. 4QCECh. 11.8 - Prob. 5QCECh. 11.8 - Convert from rectangular to cylindrical...Ch. 11.8 - Convert from rectangular to cylindrical...Ch. 11.8 - Convert from cylindrical to rectangular...Ch. 11.8 - Convert from cylindrical to rectangular...Ch. 11.8 - Convert from rectangular to spherical coordinates....Ch. 11.8 - Convert from rectangular to spherical coordinates....Ch. 11.8 - Convert from spherical to rectangular coordinates....Ch. 11.8 - Convert from spherical to rectangular coordinates....Ch. 11.8 - Convert from cylindrical to spherical coordinates....Ch. 11.8 - Convert from cylindrical to spherical coordinates....Ch. 11.8 - Convert from spherical to cylindrical coordinates....Ch. 11.8 - Convert from spherical to cylindrical coordinates....Ch. 11.8 - Use a CAS or a programmable calculating utility to...Ch. 11.8 - Use a CAS or a programmable calculating utility to...Ch. 11.8 - Determine whether the statement is true or false....Ch. 11.8 - Prob. 16ESCh. 11.8 - Prob. 17ESCh. 11.8 - Prob. 18ESCh. 11.8 - An equation is given in cylindrical coordinates....Ch. 11.8 - An equation is given in cylindrical coordinates....Ch. 11.8 - Prob. 21ESCh. 11.8 - An equation is given in cylindrical coordinates....Ch. 11.8 - An equation is given in cylindrical coordinates....Ch. 11.8 - An equation is given in cylindrical coordinates....Ch. 11.8 - Prob. 25ESCh. 11.8 - An equation is given in cylindrical coordinates....Ch. 11.8 - An equation is given in spherical coordinates....Ch. 11.8 - An equation is given in spherical coordinates....Ch. 11.8 - An equation is given in spherical coordinates....Ch. 11.8 - An equation is given in spherical coordinates....Ch. 11.8 - An equation is given in spherical coordinates....Ch. 11.8 - An equation is given in spherical coordinates....Ch. 11.8 - An equation is given in spherical coordinates....Ch. 11.8 - An equation is given in spherical coordinates....Ch. 11.8 - Prob. 35ESCh. 11.8 - An equation of a surface is given in rectangular...Ch. 11.8 - An equation of a surface is given in rectangular...Ch. 11.8 - An equation of a surface is given in rectangular...Ch. 11.8 - An equation of a surface is given in rectangular...Ch. 11.8 - An equation of a surface is given in rectangular...Ch. 11.8 - An equation of a surface is given in rectangular...Ch. 11.8 - An equation of a surface is given in rectangular...Ch. 11.8 - Prob. 43ESCh. 11.8 - An equation of a surface is given in rectangular...Ch. 11.8 - An equation of a surface is given in rectangular...Ch. 11.8 - An equation of a surface is given in rectangular...Ch. 11.8 - Describe the region in 3-space that satisfies the...Ch. 11.8 - Describe the region in 3-space that satisfies the...Ch. 11.8 - Describe the region in 3-space that satisfies the...Ch. 11.8 - Describe the region in 3-space that satisfies the...Ch. 11.8 - St. Petersburg (Leningrad), Russia, is located at...Ch. 11.8 - (a) Show that the curve of intersection of the...Ch. 11.8 - The accompanying figure shows a right circular...Ch. 11.8 - Referring to Exercise 53, use a graphing utility...Ch. 11.8 - The shape of a natural draft cooling tower for a...Ch. 11.8 - Assuming it to be hollow, estimate the volume of...Ch. 11 - (a) What is the difference between a vector and a...Ch. 11 - (a) Sketch vectors u and v for which u+vanduv are...Ch. 11 - (a) Draw a picture that shows the direction angles...Ch. 11 - (a) Make a table that shows all possible cross...Ch. 11 - In each part, find an equation of the sphere with...Ch. 11 - Find the largest and smallest distances between...Ch. 11 - Given the points P3,4,Q1,1,andR5,2, use vector...Ch. 11 - Let u=3,5,1andv=2,2,3. Find a2u+5vb1vvcuduv.Ch. 11 - Prob. 9RECh. 11 - Let r0=x0,y0,z0andr=x,y,z. Describe the set of all...Ch. 11 - Prob. 11RECh. 11 - Find the vector with length 5 and direction angles...Ch. 11 - Assuming that force is in pounds and distance is...Ch. 11 - Assuming that force is in newtons and distance is...Ch. 11 - (a) Find the area of the triangle with vertices...Ch. 11 - True or false? Explain your reasoning....Ch. 11 - Prob. 17RECh. 11 - Prob. 18RECh. 11 - Prob. 19RECh. 11 - (a) Find parametric equations for the intersection...Ch. 11 - Find an equation of the plane that is parallel to...Ch. 11 - Find an equation of the plane through the point...Ch. 11 - What condition must the constants satisfy for the...Ch. 11 - Prob. 24RECh. 11 - In each part, identify the surface by completing...Ch. 11 - In each part, express the equation in cylindrical...Ch. 11 - In each part, express the equation in rectangular...Ch. 11 - Sketch the solid in 3-space that is described in...Ch. 11 - Sketch the solid in 3-space that is described in...Ch. 11 - Sketch the solid in 3-space that is described in...Ch. 11 - Sketch the solid in 3-space that is described in...Ch. 11 - Sketch the surface whose equation in spherical...

Additional Math Textbook Solutions

Find more solutions based on key concepts
A categorical variable has three categories, with the following frequencies of occurrence: a. Compute the perce...

Basic Business Statistics, Student Value Edition

Whether the requirements for a hypothesis test are satisfied or not.

Elementary Statistics

Siblings The histogram shows the distribution of the numbers of siblings (brothers and sisters) for 2000 adults...

Introductory Statistics

Integrals involving tan x and sec x Evaluate the following integrals. 35. tan34xdx

Calculus: Early Transcendentals (2nd Edition)

CHECK POINT I You deposit $3000 in s savings account at Yourtown Bank, which has rate of 5%. Find the interest ...

Thinking Mathematically (6th Edition)

In Exercises 1–6, determine from the graph whether the function has any absolute extreme values on [a, b]. Then...

University Calculus: Early Transcendentals (4th Edition)

Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
SEE MORE TEXTBOOKS
What is Ellipse?; Author: Don't Memorise;https://www.youtube.com/watch?v=nzwCInIMlU4;License: Standard YouTube License, CC-BY