Chapter 11.5, Problem 57P

A block of weight W is dropped from a height h onto the horizontal beam AB and hits point D. (a) Denoting by y_m the exact value of the maximum deflection at D and by y’_m the value obtained by neglecting the effect of this deflection on the change in potential energy of the block, show that the absolute value of the relative error is (y’_m — y_m)/y_m, never exceeding y^’_m /2h. (b) Check the result obtained in part a by solving part a of Prob. 11.52 without taking y_m into account when determining the change in potential energy of the load, and comparing the answer obtained in this way with the exact answer to that problem.

11.52 The 2-kg block D is dropped from the position shown onto the end of a 16-mm-diameter rod. Knowing that E = 200 GPa, determine (a) the maximum deflection of end A, (b) the maximum bending moment in the rod, (c) the maximum normal stress in the rod.

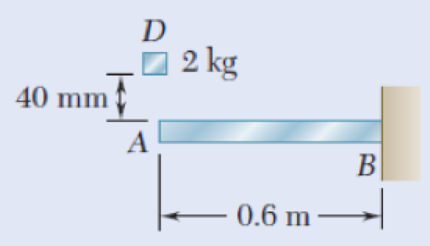
Fig. P11.52

To determine

The absolute value of the relative error $\frac{{y^{\prime }}_m-y_m}{y_m}\le \frac{{y^{\prime }}_m}{2h}$

Answer to Problem 57P

The absolute value of the relative error $\underset{\_}{\frac{{y^{\prime }}_m-y_m}{y_m}\le \frac{{y^{\prime }}_m}{2h}}$ is proved.

Explanation of Solution

Calculation:

Sketch the loading diagram as shown in Figure 1.

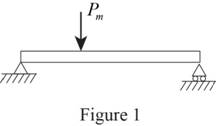
Refer to Figure 1.

Apply the spring constant k for the load applied at point D.

The load $P_m=k{y}_m$

Calculate the maximum strain energy $\left(U_m\right)$ as shown below.

$U_m=\frac{1}{2}{P}_m{y}_m$

Substitute $k{y}_m$ for $P_m$.

$\begin{array}{c}{U}_m=\frac{1}{2}k{y}_m\times y_m\\ =\frac{1}{2}k{y}_m^2\end{array}$

Calculate the work of the block exactly as shown below.

$\text{Work}=W\left(h+y_m\right)$

Calculate the work of the block approximately as shown below.

$\text{Work}=Wh$

Equating work and strain energy as shown below.

$\text{Work}=\text{Strain}\text{Energy}\left(U_m\right)$ (1)

Equating work and strain energy exactly as shown below

Substitute $\frac{1}{2}k{y}_m^2$ for $U_m$ and $W\left(h+y_m\right)$ for $\text{Work}$ in Equation (1).

$\begin{array}{l}\frac{1}{2}k{y}_m^2=W\left(h+y_m\right)\\ \frac{1}{2}k{y}_m^2=Wh+W{y}_m\end{array}$ (2)

Equating work and strain energy exactly as shown below

Substitute $\frac{1}{2}k{y^{\prime }}_m^2$ for $U_m$ and $Wh$ for $\text{Work}$ in Equation (1).

$\frac{1}{2}k{y^{\prime }}_m^2=Wh$ (3)

Here, ${y^{\prime }}_m$ is the approximate value of $y_m$.

$\begin{array}{l}\frac{{y^{\prime }}_m^2}{h}=\frac{2W}{k}\\ {y^{\prime }}_m^2=\frac{2Wh}{k}\\ {y^{\prime }}_m=\sqrt{\frac{2Wh}{k}}\end{array}$ (4)

Subtracting Equation (3) from Equation (2) as shown below.

$\begin{array}{l}\frac{1}{2}k{y}_m^2-\frac{1}{2}k{y^{\prime }}_m^2=Wh+W{y}_m-Wh\\ \frac{1}{2}k\left(y_m^2-{y^{\prime }}_m^2\right)=W{y}_m\\ \frac{1}{2}k\left(y_m-{y^{\prime }}_m\right)\left(y_m+{y^{\prime }}_m\right)=W{y}_m\\ \frac{y_m-{y^{\prime }}_m}{y_m}=\frac{2W}{k\left(y_m+{y^{\prime }}_m\right)}\end{array}$

Here, $\frac{y_m-{y^{\prime }}_m}{y_m}$ is the relative error

Substitute $\frac{{y^{\prime }}_m^2}{h}$ for $\frac{2W}{k}$.

$\begin{array}{c}\frac{y_m-{y^{\prime }}_m}{y_m}=\frac{1}{\left(y_m+{y^{\prime }}_m\right)}\frac{{y^{\prime }}_m^2}{h}\\ =\frac{{y^{\prime }}_m^2}{h\left(y_m+{y^{\prime }}_m\right)}<\frac{{y^{\prime }}_m}{2h}\end{array}$

Hence, the absolute value of the relative error $\underset{\_}{\frac{{y^{\prime }}_m-y_m}{y_m}\le \frac{{y^{\prime }}_m}{2h}}$ is proved.

To determine

The relative error of the block.

Answer to Problem 57P

The relative error of the block is $\underset{\_}{0.152}$.

Explanation of Solution

Given information:

The mass of the block is $m=2\text{kg}$.

The modulus of elasticity is $E=200\text{GPa}$ .

The diameter of the rod is $d=16\text{mm}$.

The length of the beam is $L=0.6\text{m}$.

The dropping height is $h=40\text{mm}$.

Calculation:

Refer to part (a).

The relative error is $\frac{y_m-{y^{\prime }}_m}{y_m}$ (5)

Consider the acceleration due to gravity as $g=9.81\text{m}/{\text{s}}^2$.

Calculate the weight of the block as shown below.

$W=mg$

Substitute $2\text{kg}$ for m and $9.81\text{m}/{\text{s}}^2$ for g.

$\begin{array}{c}W=2\text{kg}\times 9.81\text{m}/{\text{s}}^2\\ =19.62\text{kg}\cdot \text{m}/{\text{s}}^2\times \frac{1\text{N}}{1\text{kg}\cdot \text{m}/{\text{s}}^2}\\ =19.62\text{N}\end{array}$

Calculate the moment of inertia $\left(I\right)$ of the rod as shown below.

$I=\frac{\pi d^4}{64}$

Substitute $16\text{mm}$ for d.

$\begin{array}{c}I=\frac{\pi \times {16}^4}{64}\\ =3,217{\text{mm}}^{\text{4}}\times {\left(\frac{1\text{m}}{1,000\text{mm}}\right)}^4\\ =3.217\times {10}^{-9}{\text{m}}^4\end{array}$

Calculate the moment of inertia $\left(I\right)$ of the rod as shown below.

$I=\frac{\pi d^4}{64}$

Substitute $16\text{mm}$ for d.

$\begin{array}{c}I=\frac{\pi \times {16}^4}{64}\\ =3,217{\text{mm}}^{\text{4}}\times {\left(\frac{1\text{m}}{1,000\text{mm}}\right)}^4\\ =3.217\times {10}^{-9}{\text{m}}^4\end{array}$

Calculate the centroid (c) of the rod as shown below.

$c=\frac{d}{2}$

Substitute $16\text{mm}$ for d.

$\begin{array}{c}c=\frac{16}{2}\\ =8\text{mm}\end{array}$

Sketch the deformation diagram as shown in Figure 2.

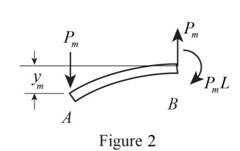
Refer to Figure 2.

Refer to Appendix D “Beam Deflections and Slope” in the text book,

Calculate the maximum deflection $\left(y_m\right)$ as shown below.

$y_m=\frac{P_m{L}^3}{3EI}$

Substitute $200\text{GPa}$ for E, $0.6\text{m}$ for L, and $3.217\times {10}^{-9}{\text{m}}^4$ for I.

$\begin{array}{c}{y}_m=\frac{P_m\times {\left(0.6\text{m}\right)}^3}{3\times 200\text{GPa}\times \frac{{10}^9\text{N}/{\text{m}}^2}{1\text{GPa}}\times 3.217\times {10}^{-9}{\text{m}}^4}\\ y_m=1.119\times {10}^{-4}{P}_m\\ P_m=8,936.6y_m\end{array}$

Calculate the maximum strain energy $\left(U_m\right)$ as shown below.

$U_m=\frac{1}{2}{P}_m{y}_m$

Substitute $8,936.6y_m$ for $P_m$.

$\begin{array}{c}{U}_m=\frac{1}{2}\times 8,936.6y_m\times y_m\\ =4,468.3y_m^2\end{array}$

Calculate the work of the block as shown below.

$\text{Work}=W\left(h+y_m\right)$

Substitute $19.62\text{N}$ for W and $40\text{mm}$ for h.

$\begin{array}{c}\text{Work}=19.62\text{N}\left(40\text{mm}\times \frac{1\text{m}}{1,000\text{mm}}+y_m\right)\\ =19.62\left(0.04+y_m\right)\\ =0.7848+19.62y_m\end{array}$

Calculate the maximum deflection $\left(y_m\right)$ as shown below.

$\text{Work}=\text{Strain}\text{Energy}\left(U_m\right)$

Substitute $4,468.3y_m^2$ for $\left(U_m\right)$ and $0.7848+19.62y_m$ for $\text{Work}$.

$\begin{array}{l}4,468.3y_m^2=0.7848+19.62y_m\\ 4,468.3y_m^2-19.62y_m-0.7848=0\\ y_m=0.015628\text{m}\times \frac{1,000\text{mm}}{1\text{m}}\\ y_m=15.63\text{mm}\end{array}$

Calculate the spring constant $\left(k\right)$ as shown below.

$k=\frac{3EI}{L^3}$

Substitute $200\text{GPa}$ for E, $0.6\text{m}$ for L, and $3.217\times {10}^{-9}{\text{m}}^4$ for I.

$\begin{array}{c}k=\frac{3\times 200\text{GPa}\times \frac{{10}^9\text{N}/{\text{m}}^2}{1\text{GPa}}\times 3.217\times {10}^{-9}{\text{m}}^4}{{\left(0.6\text{m}\right)}^3}\\ =8.936\times {10}^3\text{N}/\text{m}\end{array}$

Calculate the approximate value of $y_m$ $\left({y^{\prime }}_m\right)$ as shown below.

Substitute $19.62\text{N}$ for W, $8.936\times {10}^3\text{N}/\text{m}$ for k, and $40\text{mm}$ for h in Equation (4).

$\begin{array}{c}{y^{\prime }}_m=\sqrt{\frac{2\times 19.62\text{N}\times 40\text{mm}\times \frac{1\text{m}}{1,000\text{mm}}}{8.936\times {10}^3\text{N}/\text{m}}}\\ =\sqrt{1.7565\times {10}^{-4}}\\ =0.01325\text{m}\times \frac{1,000\text{mm}}{1\text{m}}\\ =13.25\text{mm}\end{array}$

Calculate the relative error as shown below.

Substitute $15.63\text{mm}$ for $y_m$ and $13.25\text{mm}$ for ${y^{\prime }}_m$ in Equation (5).

$\begin{array}{c}\text{Relative}\text{error}=\frac{15.63-13.25}{15.63}\\ =0.152\end{array}$

To check:

$\begin{array}{c}\frac{{y^{\prime }}_m}{2h}=\frac{13.25}{2\times 40}\\ =0.166>\text{Relative}\text{error}=0.152\end{array}$

Therefore, the relative error is $\underset{\_}{0.152}$.