Beginning and Intermediate Algebra
Beginning and Intermediate Algebra
5th Edition
ISBN: 9781259616754
Author: Julie Miller, Molly O'Neill, Nancy Hyde
Publisher: McGraw-Hill Education
bartleby

Videos

Textbook Question
Book Icon
Chapter 11.4, Problem 84PE

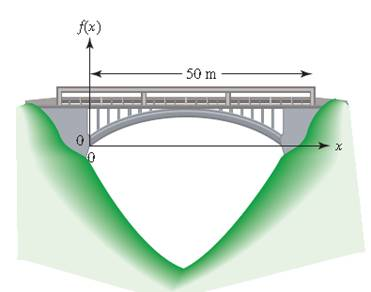
A 50-m bridge over a crevasse is supported by a parabolic arch. The function defined by f ( x ) = − 0.16 ( x − 25 ) 2 + 100 (where 0 ≤ x ≤ 50 ) approximates the height f ( x ) (in feet) of the supporting arch x meters from the end of the bridge (see figure).

a.What is the location of the vertex of the arch?

b.What is the maximum height of the arch (relative to the origin)?

Chapter 11.4, Problem 84PE, A 50-m bridge over a crevasse is supported by a parabolic arch. The function defined by f ( x ) = −

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 11.4, Problem 83PE
Next
Chapter 11.4, Problem 85PE

Chapter 11 Solutions

Beginning and Intermediate Algebra

Ch. 11.1 - Solve using the square root property. 25 a 2 = 16Ch. 11.1 - Solve using the square root property. 8 x 2 + 72 =...Ch. 11.1 - Solve using the square root property. ( t − 5 ) 2...Ch. 11.1 - Determine the value of that makes the polynomial...Ch. 11.1 - Determine the value of n that makes the polynomial...Ch. 11.1 - Prob. 6SPCh. 11.1 - Prob. 7SPCh. 11.1 - Prob. 8SPCh. 11.1 - Prob. 9SPCh. 11.1 - Prob. 10SP
Ch. 11.1 - Prob. 11SPCh. 11.1 - Prob. 12SPCh. 11.1 - Prob. 1PECh. 11.1 - Prob. 2PECh. 11.1 - Prob. 3PECh. 11.1 - Prob. 4PECh. 11.1 - Prob. 5PECh. 11.1 - Prob. 6PECh. 11.1 - Prob. 7PECh. 11.1 - Prob. 8PECh. 11.1 - Prob. 9PECh. 11.1 - Prob. 10PECh. 11.1 - Prob. 11PECh. 11.1 - Prob. 12PECh. 11.1 - Prob. 13PECh. 11.1 - Prob. 14PECh. 11.1 - Prob. 15PECh. 11.1 - Prob. 16PECh. 11.1 - Prob. 17PECh. 11.1 - Prob. 18PECh. 11.1 - Prob. 19PECh. 11.1 - Prob. 20PECh. 11.1 - Prob. 21PECh. 11.1 - 22. Given the equation , match the following...Ch. 11.1 - Prob. 23PECh. 11.1 - Prob. 24PECh. 11.1 - Prob. 25PECh. 11.1 - Prob. 26PECh. 11.1 - Prob. 27PECh. 11.1 - Prob. 28PECh. 11.1 - Prob. 29PECh. 11.1 - Prob. 30PECh. 11.1 - Prob. 31PECh. 11.1 - Prob. 32PECh. 11.1 - Prob. 33PECh. 11.1 - Prob. 34PECh. 11.1 - Prob. 35PECh. 11.1 - Prob. 36PECh. 11.1 - Prob. 37PECh. 11.1 - Prob. 38PECh. 11.1 - Prob. 39PECh. 11.1 - What types of quadratic equations can be solved by...Ch. 11.1 - Prob. 41PECh. 11.1 - Prob. 42PECh. 11.1 - Prob. 43PECh. 11.1 - Prob. 44PECh. 11.1 - Prob. 45PECh. 11.1 - Prob. 46PECh. 11.1 - Prob. 47PECh. 11.1 - Prob. 48PECh. 11.1 - Prob. 49PECh. 11.1 - Prob. 50PECh. 11.1 - Prob. 51PECh. 11.1 - Prob. 52PECh. 11.1 - Prob. 53PECh. 11.1 - Prob. 54PECh. 11.1 - Prob. 55PECh. 11.1 - Prob. 56PECh. 11.1 - Prob. 57PECh. 11.1 - Prob. 58PECh. 11.1 - Prob. 59PECh. 11.1 - Prob. 60PECh. 11.1 - Prob. 61PECh. 11.1 - Prob. 62PECh. 11.1 - Prob. 63PECh. 11.1 - Prob. 64PECh. 11.1 - Prob. 65PECh. 11.1 - Prob. 66PECh. 11.1 - Prob. 67PECh. 11.1 - Prob. 68PECh. 11.1 - A corner shelf is to be made from a triangular...Ch. 11.1 - Prob. 70PECh. 11.1 - Prob. 71PECh. 11.1 - Prob. 72PECh. 11.1 - Prob. 73PECh. 11.1 - If we ignore air resistance, the distance d ( t )...Ch. 11.2 - Solve the equation by using the quadratic formula....Ch. 11.2 - Solve the equation by using the quadratic formula....Ch. 11.2 - Steve and Tammy leave a campground, hiking on two...Ch. 11.2 - A rocket is launched the top of a 96 -ft building...Ch. 11.2 - Prob. 5SPCh. 11.2 - Use the discriminant to determine the type and...Ch. 11.2 - Use the discriminant to determine the type and...Ch. 11.2 - Use the discriminant to determine the type and...Ch. 11.2 - Given f ( x ) = x 2 + 5 x + 2 , Find the...Ch. 11.2 - Given f ( x ) = x 2 + 5 x + 2 , Find the x -and y...Ch. 11.2 - Given f ( x ) = 2 x 2 − 3 x + 5 , Find the...Ch. 11.2 - Given f ( x ) = 2 x 2 − 3 x + 5 , Find the y...Ch. 11.2 - Solve using any method. 2 t ( t − 1 ) + t 2 = 5Ch. 11.2 - Solve using any method. x 2 − 4 x = − 7Ch. 11.2 - Solve using any method. 1 5 x 2 − 4 5 x + 1 2 = 0Ch. 11.2 - Solve using any method. 4 y 2 − 13 = 0Ch. 11.2 - a. For the equation a x 2 + b x + c = 0 ( a ≠ 0 )...Ch. 11.2 - Use substitution to determine if x = − 3 + 5 is a...Ch. 11.2 - For Exercises 3–6, simplify the expression. 16 −...Ch. 11.2 - For Exercises 3–6, simplify the expression. 18 +...Ch. 11.2 - For Exercises 3–6, simplify the expression. 5. Ch. 11.2 - For Exercises 3–6, simplify the expression. 10 − −...Ch. 11.2 - For Exercises 7-8, determine whether the equation...Ch. 11.2 - For Exercises 7-8, determine whether the equation...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - Prob. 10PECh. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - Prob. 19PECh. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - Prob. 28PECh. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - Prob. 30PECh. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - For Exercises 9–34, solve the equation by using...Ch. 11.2 - Prob. 34PECh. 11.2 - For Exercises 35–38, factor the expression. Then...Ch. 11.2 - For Exercises 35–38, factor the expression. Then...Ch. 11.2 - For Exercises 35–38, factor the expression. Then...Ch. 11.2 - For Exercises 35–38, factor the expression. Then...Ch. 11.2 - The volume of a cube is 27 ft 3 . Find the lengths...Ch. 11.2 - The volume of a rectangular box is 64 ft 3 . If...Ch. 11.2 - The hypotenuse of a right triangle measures 4 in....Ch. 11.2 - The length of one leg of a right triangle is 1 cm...Ch. 11.2 - The hypotenuse of a right triangle is 10.2 m long....Ch. 11.2 - The hypotenuse of a right triangle is 17 ft long....Ch. 11.2 - The fatality rate (in fatalities per 100 million...Ch. 11.2 - The braking distance (in feet) of a car going v...Ch. 11.2 - Mitch throws a baseball straight up in the air...Ch. 11.2 - An astronaut on the moon throws a rock into the...Ch. 11.2 - For Exercises 49–56, a.Write the equation in the...Ch. 11.2 - For Exercises 49–56, a.Write the equation in the...Ch. 11.2 - For Exercises 49–56, a. Write the equation in the...Ch. 11.2 - For Exercises 49–56, a.Write the equation in the...Ch. 11.2 - For Exercises 49–56, a.Write the equation in the...Ch. 11.2 - For Exercises 49–56, a. Write the equation in the...Ch. 11.2 - For Exercises 49–56, a.Write the equation in the...Ch. 11.2 - For Exercises 49–56, a.Write the equation in the...Ch. 11.2 - For Exercises 57–62, determine the discriminant....Ch. 11.2 - For Exercises 57–62, determine the discriminant....Ch. 11.2 - For Exercises 57–62, determine the discriminant....Ch. 11.2 - For Exercises 57–62, determine the discriminant....Ch. 11.2 - For Exercises 57–62, determine the discriminant....Ch. 11.2 - For Exercises 57–62, determine the discriminant....Ch. 11.2 - For Exercises 63–68, find the x- and y-intercepts...Ch. 11.2 - For Exercises 63–68, find the x- and y-intercepts...Ch. 11.2 - For Exercises 63–68, find the x- and y-intercepts...Ch. 11.2 - For Exercises 63–68, find the x- and y-intercepts...Ch. 11.2 - For Exercises 63–68, find the x- and y-intercepts...Ch. 11.2 - For Exercises 63–68, find the x- and y-intercepts...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - Prob. 83PECh. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - For Exercises 69–86, solve the quadratic equation...Ch. 11.2 - Sometimes students shy away from completing the...Ch. 11.2 - Sometimes students shy away from completing the...Ch. 11.2 - 89. Graph . Compare the x-intercepts with the...Ch. 11.2 - Graph Y 1 = 64 x 3 + 1 . Compare the x-intercepts...Ch. 11.2 - Graph Y 1 = 3 x 3 − 6 x 2 + 6 x . Compare the...Ch. 11.2 - 92. Graph . Compare the x-intercepts with the...Ch. 11.3 - Solve the equation. 1. Ch. 11.3 - Solve the equation. y 2 / 3 − y 1 / 3 = 12Ch. 11.3 - Solve the equation. z − z − 2 = 0Ch. 11.3 - Solve the equation. 9 x 4 + 35 x 2 − 4 = 0Ch. 11.3 - Solve the equation. 5. Ch. 11.3 - 1. a. An equation that can be written in the form...Ch. 11.3 - For Exercises 2–7, solve the quadratic equations....Ch. 11.3 - For Exercises 2–7, solve the quadratic...Ch. 11.3 - For Exercises 2–7, solve the quadratic equations....Ch. 11.3 - For Exercises 2–7, solve the quadratic equations....Ch. 11.3 - For Exercises 2–7, solve the quadratic equations....Ch. 11.3 - For Exercises 2–7, solve the quadratic equations....Ch. 11.3 - a. Solve the quadratic equation by factoring. u 2...Ch. 11.3 - 9. a. Solve the quadratic equation by factoring....Ch. 11.3 - a. Solve the quadratic equation by factoring. u 2...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - For Exercises 11–24, solve the equation by using...Ch. 11.3 - 25. In Example 3, we solved the equation by using...Ch. 11.3 - For Exercises 26–36, solve the equations. (See...Ch. 11.3 - For Exercises 26–36, solve the equations. (See...Ch. 11.3 - For Exercises 26–36, solve the equations. (See...Ch. 11.3 - For Exercises 26–36, solve the equations. (See...Ch. 11.3 - For Exercises 26–36, solve the equations. (See...Ch. 11.3 - For Exercises 26–36, solve the equations. (See...Ch. 11.3 - For Exercises 26–36, solve the equations. (See...Ch. 11.3 - For Exercises 26–36, solve the equations. (See...Ch. 11.3 - For Exercises 26–36, solve the equations. (See...Ch. 11.3 - For Exercises 26–36, solve the equations. (See...Ch. 11.3 - For Exercises 26–36, solve the equations. (See...Ch. 11.3 - For Exercises 37–60, solve the equations. x 4 − 16...Ch. 11.3 - For Exercises 37–60, solve the equations. t 4 −...Ch. 11.3 - For Exercises 37–60, solve the equations. ( 4 x +...Ch. 11.3 - For Exercises 37–60, solve the equations. 40. Ch. 11.3 - For Exercises 37–60, solve the equations. 4 m 4 −...Ch. 11.3 - For Exercises 37–60, solve the equations. 42. Ch. 11.3 - For Exercises 37–60, solve the equations. x 6 − 9...Ch. 11.3 - For Exercises 37–60, solve the equations. 44. Ch. 11.3 - For Exercises 37–60, solve the equations. 45. Ch. 11.3 - For Exercises 37–60, solve the equations. x 2 + 60...Ch. 11.3 - For Exercises 37–60, solve the equations. 47. Ch. 11.3 - For Exercises 37–60, solve the equations. t + 10 =...Ch. 11.3 - For Exercises 37–60, solve the equations. 2 ( t −...Ch. 11.3 - For Exercises 37–60, solve the equations. ( x + 1...Ch. 11.3 - For Exercises 37–60, solve the equations. 51. Ch. 11.3 - For Exercises 37–60, solve the equations. x 2 / 5...Ch. 11.3 - For Exercises 37–60, solve the equations. m 4 + 2...Ch. 11.3 - For Exercises 37–60, solve the equations. 2 c 4 +...Ch. 11.3 - For Exercises 37–60, solve the equations. a 3 + 16...Ch. 11.3 - For Exercises 37–60, solve the equations. b 3 + 9...Ch. 11.3 - For Exercises 37–60, solve the equations. 57. Ch. 11.3 - For Exercises 37–60, solve the equations. y 3 + 8...Ch. 11.3 - For Exercises 37–60, solve the equations. 59. Ch. 11.3 - For Exercises 37–60, solve the equations. ( 5 x +...Ch. 11.3 - a.Solve the equation x 4 + 4 x 2 + 4 = 0 . b.How...Ch. 11.3 - 62. a. Solve the equation . b. How many solutions...Ch. 11.3 - a.Solve the equation x 4 − x 3 − 6 x 2 = 0 . b.How...Ch. 11.3 - a. Solve the equation x 4 − 10 x 2 + 9 = 0 . b....Ch. 11.3 - For Exercises 1–4, solve each equation...Ch. 11.3 - For Exercises 1–4, solve each equation by...Ch. 11.3 - For Exercises 1–4, solve each equation...Ch. 11.3 - For Exercises 1–4, solve each equation...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.3 - In Exercises 5–24, we have presented all types of...Ch. 11.4 - Refer to the graph of f ( x ) = x 2 + k to...Ch. 11.4 - Graph the functions f , g ,     and   h on the...Ch. 11.4 - Refer to the graph of f ( x ) = ( x − h ) 2 to...Ch. 11.4 - Graph the functions f , g ,     and h on the same...Ch. 11.4 - 5. Graph the functions on the same coordinate...Ch. 11.4 - 6. Graph the functions on the same coordinate...Ch. 11.4 - Given the function defined by g ( x ) = 3 ( x + 1...Ch. 11.4 - Given the function defined by h ( x ) = − 1 2 ( x...Ch. 11.4 - a. The graph of a quadratic function, f ( x ) = a...Ch. 11.4 - For Exercises 2–8, solve the equations. 2. Ch. 11.4 - For Exercises 2–8, solve the equations. 3. Ch. 11.4 - For Exercises 2–8, solve the equations. 2 a + 2 =...Ch. 11.4 - For Exercises 2–8, solve the equations. 5 t ( t −...Ch. 11.4 - For Exercises 2–8, solve the equations. 6. Ch. 11.4 - For Exercises 2–8, solve the equations. 7. Ch. 11.4 - For Exercises 2–8, solve the equations. 8. Ch. 11.4 - Describe how the value of k affects the graph of a...Ch. 11.4 - For Exercises 10–17, graph the functions. (See...Ch. 11.4 - For Exercises 10–17, graph the functions. (See...Ch. 11.4 - For Exercises 10–17, graph the functions. (See...Ch. 11.4 - For Exercises 10–17, graph the functions. (See...Ch. 11.4 - For Exercises 10–17, graph the functions. (See...Ch. 11.4 - For Exercises 10–17, graph the functions. (See...Ch. 11.4 - For Exercises 10–17, graph the functions. (See...Ch. 11.4 - For Exercises 10–17, graph the functions. (See...Ch. 11.4 - Describe how the value of h affects the graph of a...Ch. 11.4 - For Exercises 19–26, graph the functions. (See...Ch. 11.4 - For Exercises 19–26, graph the functions. (See...Ch. 11.4 - For Exercises 19–26, graph the functions. (See...Ch. 11.4 - For Exercises 19–26, graph the functions. (See...Ch. 11.4 - For Exercises 19–26, graph the functions. (See...Ch. 11.4 - For Exercises 19–26, graph the functions. (See...Ch. 11.4 - For Exercises 19–26, graph the functions. (See...Ch. 11.4 - For Exercises 19–26, graph the functions. (See...Ch. 11.4 - Describe how the value of a affects the graph of a...Ch. 11.4 - 28. How do you determine whether the graph of a...Ch. 11.4 - For Exercises 29–36, graph the functions. (See...Ch. 11.4 - For Exercises 29–36, graph the functions. (See...Ch. 11.4 - For Exercises 29–36, graph the functions. (See...Ch. 11.4 - For Exercises 29–36, graph the functions. (See...Ch. 11.4 - For Exercises 29–36, graph the functions. (See...Ch. 11.4 - For Exercises 29–36, graph the functions. (See...Ch. 11.4 - For Exercises 29–36, graph the functions. (See...Ch. 11.4 - For Exercises 29–36, graph the functions. (See...Ch. 11.4 - For Exercises 37–44, match the function with its...Ch. 11.4 - For Exercises 37–44, match the function with its...Ch. 11.4 - For Exercises 37–44, match the function with its...Ch. 11.4 - For Exercises 37–44, match the function with its...Ch. 11.4 - For Exercises 37–44, match the function with its...Ch. 11.4 - For Exercises 37–44, match the function with its...Ch. 11.4 - For Exercises 37–44, match the function with its...Ch. 11.4 - For Exercises 37–44, match the function with its...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - For Exercises 45–64, graph the parabola and the...Ch. 11.4 - Compare the graphs of the following equations to...Ch. 11.4 - 66. Compare the graphs of the following equations...Ch. 11.4 - For Exercises 67–78, write the coordinates of the...Ch. 11.4 - For Exercises 67–78, write the coordinates of the...Ch. 11.4 - For Exercises 67–78, write the coordinates of the...Ch. 11.4 - For Exercises 67–78, write the coordinates of the...Ch. 11.4 - For Exercises 67–78, write the coordinates of the...Ch. 11.4 - For Exercises 67–78, write the coordinates of the...Ch. 11.4 - For Exercises 67–78, write the coordinates of the...Ch. 11.4 - For Exercises 67–78, write the coordinates of the...Ch. 11.4 - For Exercises 67–78, write the coordinates of the...Ch. 11.4 - For Exercises 67–78, write the coordinates of the...Ch. 11.4 - For Exercises 67–78, write the coordinates of the...Ch. 11.4 - For Exercises 67–78, write the coordinates of the...Ch. 11.4 - 79. True or false: The function defined by has a...Ch. 11.4 - 80. True or false: The function defined by has a...Ch. 11.4 - 81. True or false: If the vertex represents a...Ch. 11.4 - True or false: If the vertex ( − 2 , 8 )...Ch. 11.4 - Prob. 83PECh. 11.4 - A 50-m bridge over a crevasse is supported by a...Ch. 11.4 - Prob. 85PECh. 11.5 - 1. Given: a. Write the function in the form...Ch. 11.5 - Prob. 2SPCh. 11.5 - Given: f ( x ) = x 2 + 4 x + 6 a. Use the vertex...Ch. 11.5 - 4. An object is launched into the air with an...Ch. 11.5 - Write an equation of the parabola that passes...Ch. 11.5 - 1. a. Given (a ≠ 0), the vertex formula gives the...Ch. 11.5 - How does the graph of f ( x ) = − 2 x 2 compare...Ch. 11.5 - How does the graph of p ( x ) = 1 4 x 2 compare...Ch. 11.5 - How does the graph of Q ( x ) = x 2 − 8 3 compare...Ch. 11.5 - How does the graph of r ( x ) = x 2 + 7 compare...Ch. 11.5 - How does the graph of s ( x ) = ( x − 4 ) 2...Ch. 11.5 - How does the graph of t ( x ) = ( x + 10 ) 2...Ch. 11.5 - Find the coordinates of the vertex of the parabola...Ch. 11.5 - For Exercises 9–16, find the value of n to...Ch. 11.5 - For Exercises 9–16, find the value of n to...Ch. 11.5 - For Exercises 9–16, find the value of n to...Ch. 11.5 - For Exercises 9–16, find the value of n to...Ch. 11.5 - For Exercises 9–16, find the value of n to...Ch. 11.5 - For Exercises 9–16, find the value of n to...Ch. 11.5 - For Exercises 9–16, find the value of n to...Ch. 11.5 - For Exercises 9–16, find the value of n to...Ch. 11.5 - For Exercises 17–28, write the function in the...Ch. 11.5 - For Exercises 17–28, write the function in the...Ch. 11.5 - For Exercises 17–28, write the function in the...Ch. 11.5 - For Exercises 17–28, write the function in the...Ch. 11.5 - For Exercises 17–28, write the function in the...Ch. 11.5 - For Exercises 17–28, write the function in the...Ch. 11.5 - For Exercises 17–28, write the function in the...Ch. 11.5 - For Exercises 17–28, write the function in the...Ch. 11.5 - For Exercises 17–28, write the function in the...Ch. 11.5 - For Exercises 17–28, write the function in the...Ch. 11.5 - For Exercises 17–28, write the function in the...Ch. 11.5 - For Exercises 17–28, write the function in the...Ch. 11.5 - For Exercises 29–40, find the vertex by using the...Ch. 11.5 - For Exercises 29–40, find the vertex by using the...Ch. 11.5 - For Exercises 29–40, find the vertex by using the...Ch. 11.5 - For Exercises 29–40, find the vertex by using the...Ch. 11.5 - For Exercises 29–40, find the vertex by using the...Ch. 11.5 - For Exercises 29–40, find the vertex by using the...Ch. 11.5 - For Exercises 29–40, find the vertex by using the...Ch. 11.5 - For Exercises 29–40, find the vertex by using the...Ch. 11.5 - For Exercises 29–40, find the vertex by using the...Ch. 11.5 - For Exercises 29–40, find the vertex by using the...Ch. 11.5 - For Exercises 29–40, find the vertex by using the...Ch. 11.5 - For Exercises 29–40, find the vertex by using the...Ch. 11.5 - For Exercises 41–44, find the vertex two ways:...Ch. 11.5 - For Exercises 41–44, find the vertex two ways:...Ch. 11.5 - For Exercises 41–44, find the vertex two ways:...Ch. 11.5 - For Exercises 41–44, find the vertex two ways:...Ch. 11.5 - For Exercises 45–52 a. Find the vertex. b. Find...Ch. 11.5 - For Exercises 45–52 a. Find the vertex. b. Find...Ch. 11.5 - For Exercises 45–52 a.Find the vertex. b.Find the...Ch. 11.5 - For Exercises 45–52 a.Find the vertex. b.Find the...Ch. 11.5 - For Exercises 45–52 a. Find the vertex. b. Find...Ch. 11.5 - For Exercises 45–52 a.Find the vertex. b.Find the...Ch. 11.5 - For Exercises 45–52 a.Find the vertex. b.Find the...Ch. 11.5 - For Exercises 45–52 a.Find the vertex. b.Find the...Ch. 11.5 - A set of fireworks mortar shells is launched from...Ch. 11.5 - 54. A baseball player throws a ball, and the...Ch. 11.5 - Gas mileage depends in part on the speed of the...Ch. 11.5 - Gas mileage depends in part on the speed of the...Ch. 11.5 - The Clostridium tetani bacterium is cultured to...Ch. 11.5 - The bacterium Pseudomonas aeruginosa is cultured...Ch. 11.5 - For Exercises 59–64, use the standard form of a...Ch. 11.5 - For Exercises 59–64, use the standard form of a...Ch. 11.5 - For Exercises 59–64, use the standard form of a...Ch. 11.5 - For Exercises 59–64, use the standard form of a...Ch. 11.5 - For Exercises 59–64, use the standard form of a...Ch. 11.5 - For Exercises 59–64, use the standard form of a...Ch. 11.5 - A farmer wants to fence a rectangular corral...Ch. 11.5 - A veterinarian wants to construct two equal-sized...Ch. 11.5 - For Exercises 67–72, graph the functions in...Ch. 11.5 - For Exercises 67–72, graph the functions in...Ch. 11.5 - For Exercises 67–72, graph the functions in...Ch. 11.5 - For Exercises 67–72, graph the functions in...Ch. 11.5 - For Exercises 67–72, graph the functions in...Ch. 11.5 - For Exercises 67–72, graph the functions in...Ch. 11 - Creating a Quadratic Model of the Form y = a ( x −...Ch. 11 - Creating a Quadratic Model of the Form y = a ( x −...Ch. 11 - Creating a Quadratic Model of the Form y = a ( x −...Ch. 11 - Creating a Quadratic Model of the Form y = a ( x −...Ch. 11 - Creating a Quadratic Model of the Form Estimated...Ch. 11 - Creating a Quadratic Model of the Form Estimated...Ch. 11 - Creating a Quadratic Model of the Form y = a ( x −...Ch. 11 - For Exercises 1–8, solve the equations by using...Ch. 11 - For Exercises 1–8, solve the equations by using...Ch. 11 - For Exercises 1–8, solve the equations by using...Ch. 11 - For Exercises 1–8, solve the equations by using...Ch. 11 - For Exercises 1–8, solve the equations by using...Ch. 11 - For Exercises 1–8, solve the equations by using...Ch. 11 - For Exercises 1–8, solve the equations by using...Ch. 11 - For Exercises 1–8, solve the equations by using...Ch. 11 - Prob. 9RECh. 11 - Use the square root property to find the length of...Ch. 11 - Prob. 11RECh. 11 - For Exercises 12–15, find the value of n so that...Ch. 11 - For Exercises 12–15, find the value of n so that...Ch. 11 - For Exercises 12–15, find the value of n so that...Ch. 11 - For Exercises 12–15, find the value of n so that...Ch. 11 - For Exercises 16–21, solve the equation by...Ch. 11 - For Exercises 16–21, solve the equation by...Ch. 11 - For Exercises 16–21, solve the equation by...Ch. 11 - For Exercises 16–21, solve the equation by...Ch. 11 - For Exercises 16–21, solve the equation by...Ch. 11 - For Exercises 16–21, solve the equation by...Ch. 11 - Solve for r. V = π r 2 h ( r > 0 )Ch. 11 - Solve for s. A = 6 s 2 ( s > 0 )Ch. 11 - Prob. 24RECh. 11 - For Exercises 25–30, determine the type (rational,...Ch. 11 - For Exercises 25–30, determine the type (rational,...Ch. 11 - For Exercises 25–30, determine the type (rational,...Ch. 11 - For Exercises 25–30, determine the type (rational,...Ch. 11 - For Exercises 25–30, determine the type (rational,...Ch. 11 - For Exercises 25–30, determine the type (rational,...Ch. 11 - For Exercises 31–38, solve the equations by using...Ch. 11 - For Exercises 31–38, solve the equations by using...Ch. 11 - For Exercises 31–38, solve the equations by using...Ch. 11 - For Exercises 31–38, solve the equations by using...Ch. 11 - For Exercises 31–38, solve the equations by using...Ch. 11 - For Exercises 31–38, solve the equations by using...Ch. 11 - For Exercises 31–38, solve the equations by using...Ch. 11 - For Exercises 31–38, solve the equations by using...Ch. 11 - For Exercises 39–42, solve using any method. 3 x 2...Ch. 11 - For Exercises 39–42, solve using any method. w 8 −...Ch. 11 - For Exercises 39–42, solve using any method. y 2 +...Ch. 11 - For Exercises 39–42, solve using any method. ( a +...Ch. 11 - The landing distance that a certain plane will...Ch. 11 - Prob. 44RECh. 11 - 45. A custom-built kitchen island is in the shape...Ch. 11 - Lincoln, Nebraska, Kansas City, Missouri, and...Ch. 11 - For Exercises 47–56, solve the equations. x − 4 x...Ch. 11 - For Exercises 47–56, solve the equations. 48. Ch. 11 - For Exercises 47–56, solve the equations.   y 4 −...Ch. 11 - For Exercises 47–56, solve the equations. 50. Ch. 11 - For Exercises 47–56, solve the equations. 51. Ch. 11 - For Exercises 47–56, solve the equations. p 2 / 5...Ch. 11 - For Exercises 47–56, solve the equations. 2 t t +...Ch. 11 - For Exercises 47–56, solve the equations. 1 m − 2...Ch. 11 - For Exercises 47–56, solve the equations. 55. Ch. 11 - For Exercises 47–56, solve the equations. ( x 2 −...Ch. 11 - For Exercises 57–64, graph the function and write...Ch. 11 - For Exercises 57–64, graph the function and write...Ch. 11 - For Exercises 57–64, graph the function and write...Ch. 11 - For Exercises 57–64, graph the function and write...Ch. 11 - For Exercises 57–64, graph the function and write...Ch. 11 - For Exercises 57–64, graph the function and write...Ch. 11 - For Exercises 57–64, graph the function and write...Ch. 11 - For Exercises 57–64, graph the function and write...Ch. 11 - For Exercises 65–66, write the coordinates of the...Ch. 11 - For Exercises 65–66, write the coordinates of the...Ch. 11 - For Exercises 67–68, write the equation of the...Ch. 11 - For Exercises 67–68, write the equation of the...Ch. 11 - For Exercises 69–72, write the function in the...Ch. 11 - For Exercises 69–72, write the function in the...Ch. 11 - For Exercises 69–72, write the function in the...Ch. 11 - For Exercises 69–72, write the function in the...Ch. 11 - For Exercises 73–76, find the coordinates of the...Ch. 11 - For Exercises 73–76, find the coordinates of the...Ch. 11 - For Exercises 73–76, find the coordinates of the...Ch. 11 - For Exercises 73–76, find the coordinates of the...Ch. 11 - For the quadratic equation y = 3 4 x 2 − 3 x , a....Ch. 11 - For the quadratic equation y = − ( x + 2 ) 2 + 4 ,...Ch. 11 - Prob. 79RECh. 11 - Prob. 80RECh. 11 - Write an equation of a parabola that passes...Ch. 11 - Prob. 82RECh. 11 - Prob. 1TCh. 11 - Prob. 2TCh. 11 - For Exercises 1–3, solve the equation by using the...Ch. 11 - Find the value of n so that the expression is a...Ch. 11 - Prob. 5TCh. 11 - Prob. 6TCh. 11 - Prob. 7TCh. 11 - Prob. 8TCh. 11 - Prob. 9TCh. 11 - Prob. 10TCh. 11 - The base of a triangle is 3 ft less than twice the...Ch. 11 - Prob. 12TCh. 11 - For Exercises 13–21, solve the equation. x − x − 6...Ch. 11 - Prob. 14TCh. 11 - Prob. 15TCh. 11 - Prob. 16TCh. 11 - Prob. 17TCh. 11 - Prob. 18TCh. 11 - Prob. 19TCh. 11 - Prob. 20TCh. 11 - Prob. 21TCh. 11 - Prob. 22TCh. 11 - Prob. 23TCh. 11 - Prob. 24TCh. 11 - Prob. 25TCh. 11 - Prob. 26TCh. 11 - Prob. 27TCh. 11 - Prob. 28TCh. 11 - Prob. 29TCh. 11 - Prob. 30TCh. 11 - Prob. 31TCh. 11 - Prob. 32TCh. 11 - Prob. 33TCh. 11 - Prob. 34TCh. 11 - Prob. 1CRECh. 11 - Prob. 2CRECh. 11 - Prob. 3CRECh. 11 - Prob. 4CRECh. 11 - Prob. 5CRECh. 11 - Prob. 6CRECh. 11 - Prob. 7CRECh. 11 - Prob. 8CRECh. 11 - 9. Solve the system of equations. Ch. 11 - Prob. 10CRECh. 11 - Prob. 11CRECh. 11 - Prob. 12CRECh. 11 - Prob. 13CRECh. 11 - Prob. 14CRECh. 11 - Prob. 15CRECh. 11 - Prob. 16CRECh. 11 - Prob. 17CRECh. 11 - Prob. 18CRECh. 11 - Prob. 19CRECh. 11 - Prob. 20CRECh. 11 - Prob. 21CRECh. 11 - Prob. 22CRECh. 11 - Prob. 23CRECh. 11 - Prob. 24CRECh. 11 - Prob. 25CRECh. 11 - Prob. 26CRECh. 11 - Prob. 27CRECh. 11 - Prob. 28CRE
Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Text book image
Intermediate Algebra
Algebra
ISBN:9780998625720
Author:Lynn Marecek
Publisher:OpenStax College
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Interpreting Graphs of Quadratic Equations (GMAT/GRE/CAT/Bank PO/SSC CGL) | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=BHgewRcuoRM;License: Standard YouTube License, CC-BY
Solve a Trig Equation in Quadratic Form Using the Quadratic Formula (Cosine, 4 Solutions); Author: Mathispower4u;https://www.youtube.com/watch?v=N6jw_i74AVQ;License: Standard YouTube License, CC-BY