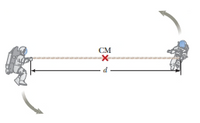
Two astronauts (Fig. P11.39), each having a mass M, are connected by a rope of length d having negligible mass. They are isolated in space, orbiting their center of mass at speeds v. Treating the astronauts as particles, calculate (a) the magnitude of the angular momentum of the two-astronaut system and (b) the rotational energy of the system. By pulling on the rope, one of the astronauts shortens the distance between them to d/2. (c) What is the new angular momentum of the system? (d) What are the astronauts' new speeds? (e) What is the new rotational energy of the system? (f) How much potential energy in the body of the astronaut was converted to mechanical energy in the system when he shortened the rope? Figure P11.39 Problems 39 and 40.

Two 3.50 kg balls are attached to the ends of a thin rod of length 36.0 cm and negligible mass. The rod is free to rotate in a vertical plane without friction about a horizontal axis through its center. With the rod initially horizontal (the figure), a 42.0 g wad of wet putty drops onto one of the balls, hitting it with a speed of 3.25 m/s and then sticking to it. (a) What is the angular speed of the system just after the putty wad hits? (b) What is the ratio of the kinetic energy of the system after the collision to that of the putty wad just before? (c) Through what angle (deg) will the system rotate before it momentarily stops? Putty wad Rotation axis

A 45 kg figure skater is spinning on the toes of her skates at 1.3 rev/s. Her arms are outstretched as far as they will go. In this orientation, the skater can be modeled as a cylindrical torso (40 kg, 20 cm average diameter, 160 cm tall) plus two rod-like arms (2.5 kg each, 71 cm long) attached to the outside of the torso. The skater then raises her arms straight above her head. In this latter orientation, she can be modeled as a 45 kg, 20-cm-diameter, 200-cm-tall cylinder. Part A What is her new rotation frequency, in revolutions per second? Express your answer in revolutions per second. ► View Available Hint(s) W₂ Submit Provide Feedback ΑΣΦ ? rev/s

Two 4.80 kg balls are attached to the ends of a thin rod of length 40.0 cm and negligible mass. The rod is free to rotate in a vertical plane without friction about a horizontal axis through its center. With the rod initially horizontal (the figure), a 690 g wad of wet putty drops onto one of the balls, hitting it with a speed of 4.21 m/s and then sticking to it. (a) What is the angular speed of the system just after the putty wad hits? (b) What is the ratio of the kinetic energy of the system after the collision to that of the putty wad just before? (c) Through what angle (deg) will the system rotate before it momentarily stops? Putry wad Rotation axis (a) Number Units (b) Number Units (c) Number Units

A woman with mass 50 kg is standing on the rim of a large horizontal disk that is rotating at 0.80 rev/s about an axis through its center. The disk has mass 110 kg and radius 4.1 m. Calculate the magnitude of the total angular momentum of the woman–disk system. (Assume that you can treat the woman as a point.)

A person of mass m = 75 kg stands in the center of a large rotating disk with radius R = 5.0 m and total mass M. The rotates without friction and without any external torque, initially at an angular velocity of w. The moment of inertia of a disk is MR. Assume that the person can be approximated as point-like, i.e. the angular momentum is r x p. The person then walks radially outward. (a) What is the angular momentum of the system (person + disk) as a function of the person's radius, r, from the center? Write it in terms of m, M, R, and w. (b) If the disk is initially rotating at wo and it slows to wp =0.8 rad/s when the person is at the very edge, what is the mass of the disk? 1.1 rad/s when the person is in the exact center, (c) What is the rotational kinetic energy of the system before and after the person walks to the edge?