1 Functions And Models 2 Limits And Derivatives 3 Differentiation Rules 4 Applications Of Differentiation 5 Integrals 6 Applications Of Integration 7 Techniques Of Integration 8 Further Applications Of Integration 9 Differential Equations 10 Parametric Equations And Polar Coordinates 11 Sequences, Series, And Power Series 12 Vectors And The Geometry Of Space 13 Vector Functions 14 Partial Derivatives 15 Multiple Integrals 16 Vector Calculus A Numbers, Inequalities, And Absolute Values B Coordinate Geometry And Lines C Graphs Of Second-degree Equations D Trigonometry E Sigma Notation F Proofs Of Theorems G The Logarithm Defined As An Integral expand_more
11.1 Sequences 11.2 Series 11.3 The Integral Test And Estimates Of Sums 11.4 The Comparison Tests 11.5 Alternating Series And Absolute Convergence 11.6 The Ratio And Root Tests 11.7 Strategy For Testing Series 11.8 Power Series 11.9 Representations Of Functions As Power Series 11.10 Taylor And Maclaurin Series 11.11 Applications Of Taylor Polynomials Chapter Questions expand_more
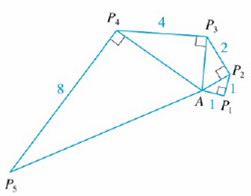
Problem 1CC: (a) What is a convergent sequence? (b) What is a convergent series? (c) What does limnan= 3 mean?... Problem 2CC Problem 3CC Problem 4CC: Suppose an=3 and sn, is the nth partial sum of the series. What is limnan? What is limn sn? Problem 5CC Problem 6CC Problem 7CC Problem 8CC Problem 9CC Problem 10CC Problem 11CC Problem 12CC: Write the binomial series expansion of ( 1 + x)k. What is the radius of convergence of this series? Problem 1TFQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 2TFQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 3TFQ Problem 4TFQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 5TFQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 6TFQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 7TFQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 8TFQ Problem 9TFQ Problem 10TFQ Problem 11TFQ Problem 12TFQ Problem 13TFQ Problem 14TFQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 15TFQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 16TFQ Problem 17TFQ Problem 18TFQ Problem 19TFQ Problem 20TFQ Problem 21TFQ Problem 22TFQ: Determine whether the statement is true or false. If it is true, explain why. If it is false,... Problem 1E: Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. 1.... Problem 2E: Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. 2.... Problem 3E: Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. 3.... Problem 4E: Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. 4.... Problem 5E Problem 6E Problem 7E: Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. 7.... Problem 8E: Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. 8.... Problem 9E Problem 10E Problem 11E: Determine whether the series is convergent or divergent. 11. n=1nn3+1 Problem 12E: Determine whether the series is convergent or divergent. 12. n=1n2+1n3+1 Problem 13E: Determine whether the series is convergent or divergent. 13. n=1n35n Problem 14E: Determine whether the series is convergent or divergent. 14. n=1(1)nn+1 Problem 15E: Determine whether the series is convergent or divergent. 15. n=21nlnn Problem 16E: Determine whether the series is convergent or divergent. 16. n=1ln(n3n+1) Problem 17E Problem 18E Problem 19E Problem 20E Problem 21E Problem 22E: Determine whether the series is convergent or divergent. 22. n=1n+1n1n Problem 23E Problem 24E: Determine whether the series is conditionally convergent, absolutely convergent, or divergent.... Problem 25E: Determine whether the series is conditionally convergent, absolutely convergent, or divergent. 25.... Problem 26E: Determine whether the series is conditionally convergent, absolutely convergent, or divergent.... Problem 27E: Find the sum of the series. 27. n=1(3)n123n Problem 28E: Find the sum of the series. 28. n=11n(n+3) Problem 29E Problem 30E Problem 31E Problem 32E Problem 33E: Show that cosh x1+12x2 for all x. Problem 34E Problem 35E Problem 36E Problem 37E Problem 38E Problem 39E Problem 40E: Find the radius of convergence and interval of convergence of the series. 40. n=1(1)nxnn25n Problem 41E: Find the radius of convergence and interval of convergence of the series. 41. n=1(x+2)nn4n Problem 42E Problem 43E Problem 44E Problem 45E Problem 46E Problem 47E: Find the Maclaurin series for f and the associated radius of convergence. You may use either the... Problem 48E: Find the Maclaurin series for f and the associated radius of convergence. You may use either the... Problem 49E: Find the Maclaurin series for f and the associated radius of convergence. You may use either the... Problem 50E Problem 51E Problem 52E: Find the Maclaurin series for f and the associated radius of convergence. You may use either the... Problem 53E Problem 54E Problem 55E Problem 56E Problem 57E Problem 58E Problem 59E Problem 60E Problem 61E Problem 62E Problem 1P Problem 2P: Let {Pn} be a sequence of points determined as in the figure. Thus |AP1|=1, |PnPn+1|=2n1, and angle... Problem 3P Problem 4P Problem 5P Problem 6P Problem 7P Problem 8P Problem 9P: Find the interval of convergence of n=1n3xn and find its sum. Problem 10P: Suppose you have a large supply of books, all the same size, and you stack them at the edge of a... Problem 11P: Find the sum of the series n=2ln(11n2). Problem 12P Problem 13P Problem 14P Problem 15P Problem 16P Problem 17P Problem 18P Problem 19P Problem 20P Problem 21P Problem 22P: (a) Show that the Maclaurin series of the function f(x)=x1xx2isn=1fnxn wherefn is the nth Fibonacci... Problem 23P: Let u=1+x33!+x66!+x99!+v=x+x44!+x77!+x1010!+w=x22!+x55!+x88!+ Show that u3 + v3 + w3 3uvw = 1. Problem 24P format_list_bulleted


 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning




