
Determine the moments at A,B, and C, then draw the moment diagram for the beam. The moment of inertia of each span is indicated in the figure. Assume the support at B is a roller and A and C are fixed. E = 29(103) ksi.
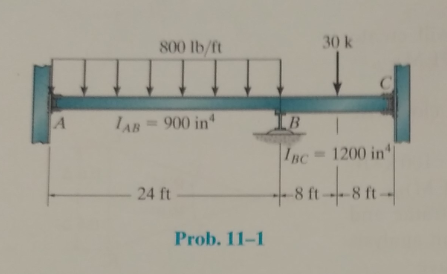
The moments at A, B, and C, and to draw the moment diagram for the beam.
Answer to Problem 11.1P
The moment at A for member AB is,
The moment at B for member BA is,
The moment at B for member BC is,
The moment at C for member CB is,
The following figure shows the moment diagram of the beam.
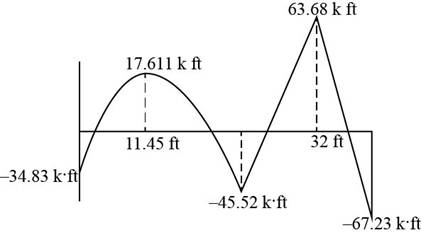
Explanation of Solution
Calculation:
The following figure shows the beam diagram.
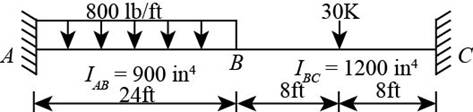
Figure-(1)
Calculate the fixed end moments at every end as shown below.
Calculate fixed end moments of member AB.
Here, given load is
Substitute
Calculate fixed end moments of member BA.
Substitute
Calculate fixed end moments of member BC.
Substitute
Calculate fixed end moments of member CB.
Substitute
Calculate the member relative stiffness factors on either side of B.
Calculate relative stiffness of member BA.
Here,
Substitute
Calculate relative stiffness of member BC.
Substitute
Calculate the distribution factors for different members.
Calculate distribution factors for AB.
Calculate distribution factors for BA.
Substitute
Substitute
Calculate distribution factors for BC.
Substitute
Substitute
Calculate distribution factors for CB.
Calculate the balance moment for each member as shown below.
Calculate balance moment foe BA.
Calculate balance moment for BC.
Draw the moment distribution table as shown below.
| Joints | A | B | C | |
| Member | AB | BA | BC | CB |
| DF | | | | |
| FEM | | | | |
| Balance | - | | | - |
| Carry over moment | | | | |
| Balance | | | | |
| | | | | |
Consider the section AB as shown below.
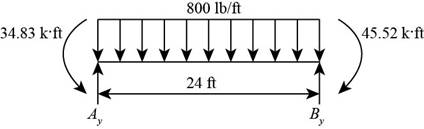
Figure-(2)
Write the Equation for sum of vertical forces.
Here, vertical reaction at A and B are
Write the Equation for sum of moment about A.
Substitute
Calculate the distance at which shear force changing its sign for maximum moment.
Write the Equation for shear force at distance
Equate the value of shear force to zero for distance.
Calculate the value of maximum moment at a distance of
Consider the section BC as shown below.
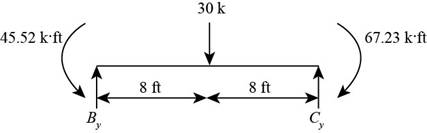
Figure-(3)
Write the Equation for sum of vertical forces.
Write the Equation for sum of moment about B.
Here, vertical reaction at C is
Substitute
For member BC, moment will be maximum at the center.
Calculate maximum moment at the center of BC.
Conclusion:
The moment at A for member AB is,
The moment at B for member BA is,
The moment at B for member BC is,
The moment at C for member CB is,
The following diagram shows the moment diagram of the beam.
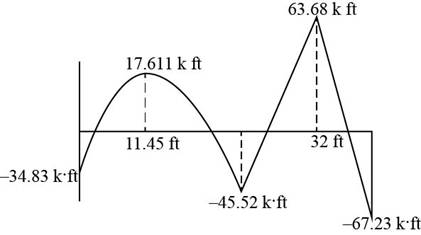
Figure-(4)
Want to see more full solutions like this?
Chapter 11 Solutions
Structural Analysis (10th Edition)
Additional Engineering Textbook Solutions
Elementary Surveying: An Introduction To Geomatics (15th Edition)
Database Concepts (8th Edition)
Java: An Introduction to Problem Solving and Programming (8th Edition)
Web Development and Design Foundations with HTML5 (8th Edition)
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
- subjectarrow_forwardExample 5.2: Design Example of a Square Foundation for a Colum Figure A.3a shows a square column foundation with the followin conditions: Live load=L=675 kN Dead load D= 1125 kN Allowable gross soil-bearing capacity 145 kN/m² Column size-0.5 m x 0.5 m -20.68 MN/m² 1,413.7 MN/m² Let it be required to design the column foundation. 1.25m-D L-675 AN D-1125 AN (a) Column section- 05 m x 0.5marrow_forwardExample 5.3: Design Example of a Rectangular Foundation for Column This section describes the design of a rectangular foundation to support a column having dimensions of 0.4 m x 0.4 m in cross section. Other details are as follows: Dead load D= 290 kN Live load L= 110 kN Depth from the ground surface to the top of the foundation = 1.2 m Allowable gross soil-bearing capacity = 120 kN/m² Maximum width of foundation = B = 1.5 m f, = 413.7 MN/m² f=20.68 MN/m² Unit weight of soil = y = 17.27 kN/m³ Unit weight of concrete = y₁ = 22.97 kN/m³ General Considerations For this design, let us assume a foundation thickness of 0.45 m (Figure A.4a). The weight of foundation/m² = 0.45 y = (0.45) (22.97) = 10.34 kN/m², and the weight of soil above the foundation/m² = (1.2)y = (1.2) (17.27) = 20.72 kN/m² Hence, the net allowable soil- bearing capacity Iqata] =120-10.34-20.72 = 88.94 kN/m² The required area of the foundation = (D+L)/4(all) = (290 + 110)/88.94 = 4.5 m². Hence, the length of the foundation…arrow_forward
- Problem 1 You are in the process of designing a water supply system for the whole lligan City, and the design life of your system is to end in the year 2070. The population in the town has been measured every 10 years since 1980 by the Philippine Statistics Authority, and the reported populations are tabulated below. Estimate the population in the town using (a) arithmetic growth projection, (b) geometric growth projection (exponential formula), (c) declining growth projection (assuming a saturation concentration of 480,000 people), and (d) logistic curve projection. Year Population 1980 167,358 1990 226,568 2000 285,061 2010 322,821 2020 342,618arrow_forwardA frame is loaded by a force Q = 280 N and supported by pins at points B and C as shown below. The distances are given as a = 0.4 m, b = 0.8 m, c = 0.6 m, d = 2.6 m, and e = 1.5 m. b C с d a A B Q D e Determine the reactions at joints B and C. Report all answers in units of N with 2 decimal places of precision. Positive signs indicate that a force component acts in the positive axis direction (i.e. up or right), while a negative sign should be used to indicate a force component acting in a negative axis direction (i.e. down or left). The x-component of the reaction force at joint B, Bx = NⓇ The y-component of the reaction force at joint B, By = NⓇ NⓇ The x-component of the reaction force at joint C, Cx = The y-component of the reaction force at joint C, C₁ = N Numberarrow_forwardD Ø A vertical pole supports a horizontal cable CD and is supported by a ball-and-socket joint at A as shown in the figure below. Cable CD is parallel to the x-z plane (which implies that a vector from C to D has no y-component) and is oriented at an angle = 20° from the x-y plane. The distances are given as h = 10 m, b = 6 m, a = 9 m, and d = 4 m. y a b B The magnitude of the tension force in cable BE, TBE = KN ® F® Determine the following forces for this system if there is a 15 kN tension carried in cable CD. Report all answers in units of kN with 1 decimal place of precision. For the components of the reaction at A, be sure to use a positive or negative sign to indicate the direction of the force (negative signs if the force acts in the negative axial direction). The magnitude of the tension force in cable BF, TBF = KN The x-component of the reaction at joint A, Ax The y-component of the reaction at joint A, A, ®®® The z-component of the reaction at joint A, Az = = KN = KN KNarrow_forward
- (10 points) Problem 4. Suppose only through traffic is allowed on an intersection approach, and traffic arrive at a constant rate of 400 veh/h. Their effective green time is set to 15 seconds. Cycle length is 60 seconds. Estimate the average delay for that approach. Use a saturation flow rate of 1750 veh/h; D/D/1 queuing. Centenniam ad) of gy dov yasm wof ni emilarrow_forwardA vertical pole supports a horizontal cable CD and is supported by a ball-and-socket joint at A as shown in the figure below. Cable CD is parallel to the x-z plane (which implies that a vector from C to D has no y-component) and is oriented at an angle = 20° from the x-y plane. The distances are given as h = 10 m, b = 6 m, a = 9 m, and d = 4 m. D C a B Determine the following forces for this system if there is a 15 kN tension carried in cable CD. Report all answers in units of kN with 1 decimal place of precision. For the components of the reaction at A, be sure to use a positive or negative sign to indicate the direction of the force (negative signs if the force acts in the negative axial direction). The magnitude of the tension force in cable BE, TBE = KN ☑ The magnitude of the tension force in cable BF, TBF = KN The x-component of the reaction at joint A, Ax = ☑ KN The y-component of the reaction at joint A, A, = KN The z-component of the reaction at joint A, Az = KN ☑arrow_forwardA vertical pole supports a horizontal cable CD and is supported by a ball-and-socket joint at A as shown in the figure below. Cable CD is parallel to the x-z plane (which implies that a vector from C to D has no y-component) and is oriented at an angle : = 20° from the x-y plane. The distances are given as h = 10 m, b = 6 m, a = 9 m, and d = 4 m. D C a B x Determine the following forces for this system if there is a 15 kN tension carried in cable CD. Report all answers in units of kN with 1 decimal place of precision. For the components of the reaction at A, be sure to use a positive or negative sign to indicate the direction of the force (negative signs if the force acts in the negative axial direction). The magnitude of the tension force in cable BE, TBE = 4.1 KN The magnitude of the tension force in cable BF, TBF = 41.1 KN The x-component of the reaction at joint A, Ax = 309.C KN ®®®® F The y-component of the reaction at joint A, Ay = -216. KN The z-component of the reaction at…arrow_forward
- A small barrel weighing 400 N is lifted by a pair of tongs as shown. Knowing that h = 200 mm, L₁ = 400 mm, L2 = 120 mm and L3 = 200 mm, determine the magnitude of the forces exerted on member ABD of this machine structure. C L2 A P L1 L3 B D Report your answers in units of N with 2 decimal places of precision. N. The magnitude of the force acting at joint B = The magnitude of the force acting at joint D = N.arrow_forwardA frame is loaded by a force Q = 280 N and supported by pins at points B and C as shown below. The distances are given as a = 0.4 m, b = 0.8 m, c = 0.6 m, d = 2.6 m, and e = 1.5 m. b C C d 11041 A B Q C D e Determine the reactions at joints B and C. Report all answers in units of N with 2 decimal places of precision. Positive signs indicate that a force component acts in the positive axis direction (i.e. up or right), while a negative sign should be used to indicate a force component acting in a negative axis direction (i.e. down or left). The x-component of the reaction force at joint B, Bx = N The y-component of the reaction force at joint B, By = N The x-component of the reaction force at joint C, Cx = N The y-component of the reaction force at joint C, Cy == Narrow_forwardI need help drawing the digram.arrow_forward

 Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning





