
Engineering Mechanics: Statics, Student Value Edition; Modified Mastering Engineering with Pearson eText -- Standalone Access Card -- for Engineering Mechanics: Statics (14th Edition)
14th Edition
ISBN: 9780134246192
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 10.8, Problem 100P
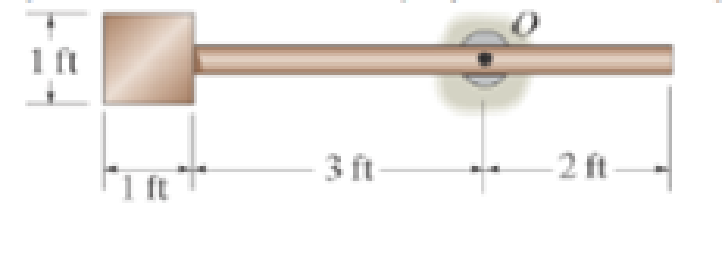
The pendulum consists of a plate having a weight of 12 lb and a slender rod having a weight of 4 lb. Determine the radius of gyration of the pendulum about an axis perpendicular to the page and passing through point O.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The pendulum is suspended from point O and consists of two bars, each weighing 10 lb. Determine the moment of inertia of the pendulum about the axis through the center of mass G.
The pendulum is suspended from point O and consists of two bars, each weighing 10 lb. Determine the moment of inertia of the pendulum about the axis through pin O.
The pendulum consists of a 6.5- kg circular plate and a 2.5- kg slender rod.
Determine the radius of gyration of the pendulum about an axis perpendicular to the page and passing through point O.
Chapter 10 Solutions
Engineering Mechanics: Statics, Student Value Edition; Modified Mastering Engineering with Pearson eText -- Standalone Access Card -- for Engineering Mechanics: Statics (14th Edition)
Ch. 10.3 - Determine the moment of inertia of the shaded area...Ch. 10.3 - Determine the moment of inertia of the shaded area...Ch. 10.3 - Determine the moment of inertia of the shaded area...Ch. 10.3 - Determine the moment of inertia of the shaded area...Ch. 10.3 - Determine the moment of inertia about the x axis.Ch. 10.3 - Determine the moment of inertia about the y axis.Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of Inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...
Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Solve the problem in two ways, using rectangular...Ch. 10.3 - Determine the moment of inertia of the area about...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia about the x axis.Ch. 10.3 - Determine the moment of inertia about the y axis.Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.3 - Prob. 23PCh. 10.3 - Determine the moment of inertia for the shaded...Ch. 10.4 - Determine the moment of inertia of the beams...Ch. 10.4 - Determine the moment of inertia of the beams...Ch. 10.4 - Determine me moment of inertia of the...Ch. 10.4 - Determine the moment of inertia of the...Ch. 10.4 - Determine the moment of inertia of the composite...Ch. 10.4 - Determine the moment of inertia of the composite...Ch. 10.4 - The moment of inertia about the y axis is 264...Ch. 10.4 - Determine the location y of the centroid of the...Ch. 10.4 - Determine,y, which locates the centroidal axis x...Ch. 10.4 - Determine the moment of inertia for the beams...Ch. 10.4 - Determine the moment of inertia for the beams...Ch. 10.4 - Determine the moment of inertia Ix of the shaded...Ch. 10.4 - Determine the moment of inertia Ix of the shaded...Ch. 10.4 - Determine the moment of inertia of the beams...Ch. 10.4 - Determine, g, which locates the centroidal axis z...Ch. 10.4 - Determine the moment of inertia about the x axis.Ch. 10.4 - Prob. 37PCh. 10.4 - Determine the moment of inertia of the shaded area...Ch. 10.4 - Determine the moment of inertia of the shaded area...Ch. 10.4 - Prob. 40PCh. 10.4 - Prob. 41PCh. 10.4 - Determine the moment of inertia of the beams...Ch. 10.4 - Prob. 43PCh. 10.4 - Prob. 44PCh. 10.4 - Determine the distance x to the centroid C of the...Ch. 10.4 - Determine the moment of inertia for the shaded...Ch. 10.4 - Determine the moment of inertia for the shaded...Ch. 10.4 - Determine the moment of inertia of the...Ch. 10.4 - Determine the moment of inertia of the...Ch. 10.4 - Prob. 50PCh. 10.4 - Determine the moment of inertia for the beams...Ch. 10.4 - Determine the moment of inertia of the area about...Ch. 10.4 - Determine the moment of inertia of the area about...Ch. 10.7 - Determine the product of inertia of the thin strip...Ch. 10.7 - Determine the product of inertia of the shaded...Ch. 10.7 - Determine the product of inertia for the shaded...Ch. 10.7 - Determine the product of inertia of the shaded...Ch. 10.7 - Determine the product of inertia for the parabolic...Ch. 10.7 - Prob. 59PCh. 10.7 - Determine the product of inertia of the shaded...Ch. 10.7 - Prob. 61PCh. 10.7 - Prob. 62PCh. 10.7 - Prob. 63PCh. 10.7 - Determine the product of inertia for the beams...Ch. 10.7 - Determine the product of inertia tor the shaded...Ch. 10.7 - Determine the product of inertia of the cross...Ch. 10.7 - Determine the location (xy) to the centroid C of...Ch. 10.7 - For the calculation, assume all comers to be...Ch. 10.7 - Determine the moments of inertia Iu, Iv and the...Ch. 10.7 - Prob. 70PCh. 10.7 - using Mohrs circle Hint. To solve find the...Ch. 10.7 - Prob. 72PCh. 10.7 - using Mohrs circle.Ch. 10.7 - Prob. 74PCh. 10.7 - using Mohrs circle.Ch. 10.7 - Prob. 76PCh. 10.7 - using Mohrs circle.Ch. 10.7 - Prob. 78PCh. 10.7 - using Mohrs circle.Ch. 10.7 - Prob. 80PCh. 10.7 - Solve Prob. 10-80 using Mohrs circle.Ch. 10.7 - Prob. 82PCh. 10.7 - Solve Prob. 10-82 using Mohrs circle.Ch. 10.8 - Determine the moment of inertia of the thin ring...Ch. 10.8 - The material has a constant density .Ch. 10.8 - Determine the radius of gyration kx of the...Ch. 10.8 - Prob. 87PCh. 10.8 - Hint: For integration, use thin plate elements...Ch. 10.8 - The material has a constant density .Ch. 10.8 - Prob. 90PCh. 10.8 - Determine the moment of inertia Iy. The specific...Ch. 10.8 - Prob. 92PCh. 10.8 - Prob. 93PCh. 10.8 - The total mass of the solid is 1500 kg.Ch. 10.8 - The slender rods have a mass of 4 kg/ point A....Ch. 10.8 - and a 4-kg slender rod. Determine the radius of...Ch. 10.8 - The material has a density of 200kg/m3. Prob....Ch. 10.8 - Determine the location y of the center of mass G...Ch. 10.8 - Prob. 99PCh. 10.8 - The pendulum consists of a plate having a weight...Ch. 10.8 - 15 lb. and 20 lb, respectively, determine the mass...Ch. 10.8 - The density of the material is 7.85 Mg/m3.Ch. 10.8 - Prob. 103PCh. 10.8 - Determine its mass moment of inertia about the y...Ch. 10.8 - Prob. 105PCh. 10.8 - Prob. 106PCh. 10.8 - Prob. 107PCh. 10.8 - The thin plate has a mass of 12 kg/m2. Determine...Ch. 10.8 - The material has a density of 200kg/m3.Ch. 10.8 - Determine the moment of inertia for the shaded...Ch. 10.8 - Determine the moment of inertia for the shaded...Ch. 10.8 - Determine the area moment of inertia of the shaded...Ch. 10.8 - Prob. 4RPCh. 10.8 - Determine the area moment of inertia of the...Ch. 10.8 - Determine the product of inertia of the shaded...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Kindly show you handwritten solution. thankyouarrow_forwardThe pendulum consists of the 3-kg slender rod and the 5-kg thin plate. Determine the location ỹ of the center of mass G of the pendulum; then calculate the moment of inertia of the pendulum about an axis perpendicular to the page and passing through G. y 2 m G 0.5 m Eim-arrow_forward2. Determine the radius of gyration kz for the column's cross-sectional area. 4d The dimension d is given. 2d 4d 4d 4d Zarrow_forward
- h y g(x) density p = 800 kg m³ Determine the cone's radius of gyration about the x-axis. 2h x An engineering student has modelled a truncated cone in CAD software by rotating the coloured area about the x-axis. The y-coordinate can be described by the equation g(x) = + 1 and the cup has constant 6 The cone has dimensions h = 1 m and l = 6 m. Xarrow_forward.Three identical uniform rods, each of length L and mass m, are joined to form a rigid equilateral triangle Its radius of gyration about an axis passing through a corner and perpendicular to the plane of the triangle is L L -| -| -S -15arrow_forwardThe wheel and attached spool have a combined weight of 50 lb and a radius of gyration about its center of kA = 6 in. If pulley B mounted on the engine is subjected to a torque M = 62.5 lb.ft, determine the total work exerted on the system if the pulley has made 9 revolutions. Shipping weight is 280 lbs. 3 in. M 3 in. M 7.5 in. 7.5 in. 4.5 in. 4.5 in.arrow_forward
- Determine the moment of inertia of mass with respect to the x' axis that passes through the structure's center of gravity and is parallel to the x axis. The cone has a density of 6000 kg/m3 and the cylinder a density of 8000 kg/m3. Consider H = 83arrow_forwardsolve it clearly and correctly. i will ratearrow_forwardA composite pendulum is made of a uniform slender rod and a uniform disk. If the rod has length of 1.3 m and mass of 13.1 kg, and the disk has radius of 0.28 m and mass of 7.0 kg, determine the radius of gyration k about the centroidal x axis. Please pay attention: the numbers may change since they are randomized. Your answer must include 3 places after the decimal point, and proper unit. y G R Profile view Your Answer: Answer unitsarrow_forward
- Please help with the attached problem.arrow_forwardFind the centre of mass of the object below. Let the lengths be: d1 = 160mm, d2 = 270 mm, d3= 200 mm, d4 = 210 mm, d5 = 300mm, d6 = 240mm.arrow_forwardThe S-shaped piece is formed from a rod of diameter d and bent into the two semicircular shapes. Determine the products of inertia for the rod, for which d is small compared with r. The total mass of the piece is m = 9.1 kg and the distance r is 395 mm. Answers: Ixy = Ixz = lyz = i i i d kg-m² kg-m² kg-m²arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L

International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Ch 2 - 2.2.2 Forced Undamped Oscillation; Author: Benjamin Drew;https://www.youtube.com/watch?v=6Tb7Rx-bCWE;License: Standard youtube license