Algebra and Trigonometry (6th Edition)
6th Edition
ISBN: 9780134463216
Author: Robert F. Blitzer
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 10.5, Problem 70E
The path of a projectile that is launched h feet above the ground with an initial velocity of t\) feet per second and at an angle 0 with the horizontal is given by the parametric equations
where t is the time, in seconds, after the projectile was launched. The parametric equation for x gives the projectile’s horizontal distance, in feet. The parametric equation for y gives the projectile’s| height, in feet. Use these parametric equations to solve Exercises 69 -70.
The figure shows the path for a baseball that was hit with an initial velocity of 150 feet per second at an angle of 35° to the horizontal. The ball was hit at a height of 3 feet off the ground.
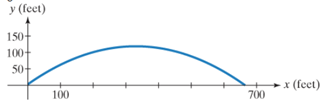
a. Find the parametric equations that describe the position of the ball as a function of time.
b. Describe the ball's position after 1, 2, and 3 seconds. Round to the nearest tenth of a foot. Locate your solutions on the plane curve.
c. How long is the ball in flight? (Round to the nearest tenth of a second. ) What is the total horizontal distance that it travels, to the nearest tenth of a foot, before it lands? Is your answer consistent with the figure shown?
d. Use the graph to describe something about the path of the baseball that might be of interest to the player who hit the ball. Then verify your observation algebraically.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Question 4
Find the value of the first element for the first row of the inverse matrix of matrix B.
3
Not yet
answered
B =
Marked out of
5.00
· (³ ;)
Flag question
7
[Provide your answer as an integer number (no fraction). For a decimal number, round your
answer to 2 decimal places]
Answer:
Question 2
Not yet
answered
Multiply the following Matrices together:
[77-4
A =
36
Marked out of
-5 -5
5.00
B =
3
5
Flag question
-6
-7
AB
Assume {u1, U2, u3, u4} does not span R³.
Select the best statement.
A. {u1, U2, u3} spans R³ if u̸4 is a linear combination of other vectors in the set.
B. We do not have sufficient information to determine whether {u₁, u2, u3} spans R³.
C. {U1, U2, u3} spans R³ if u̸4 is a scalar multiple of another vector in the set.
D. {u1, U2, u3} cannot span R³.
E. {U1, U2, u3} spans R³ if u̸4 is the zero vector.
F. none of the above
Chapter 10 Solutions
Algebra and Trigonometry (6th Edition)
Ch. 10.1 - Fill in each blank so that the resulting statement...Ch. 10.1 - Prob. 2CVCCh. 10.1 - Prob. 3CVCCh. 10.1 - Prob. 4CVCCh. 10.1 - The graph of (x+1)225+(y4)29=1 has its center...Ch. 10.1 - Prob. 6CVCCh. 10.1 - Prob. 7CVCCh. 10.1 - 8. In the equation , we complete the square on x...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - Prob. 2E
Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 1-18, graph each ellipse and locate...Ch. 10.1 - In Exercises 19-24, find the standard form of the...Ch. 10.1 - In Exercises 19-24, find the standard form of the...Ch. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECh. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Prob. 34ECh. 10.1 - Prob. 35ECh. 10.1 - Prob. 36ECh. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Prob. 39ECh. 10.1 - Prob. 40ECh. 10.1 - Prob. 41ECh. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - Prob. 46ECh. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - Prob. 49ECh. 10.1 - Prob. 50ECh. 10.1 - Prob. 51ECh. 10.1 - Prob. 52ECh. 10.1 - Prob. 53ECh. 10.1 - In Exercises 51-60, convert each equation to...Ch. 10.1 - Prob. 55ECh. 10.1 - Prob. 56ECh. 10.1 - Prob. 57ECh. 10.1 - Prob. 58ECh. 10.1 - Prob. 59ECh. 10.1 - Prob. 60ECh. 10.1 - Prob. 61ECh. 10.1 - Prob. 62ECh. 10.1 - Prob. 63ECh. 10.1 - Prob. 64ECh. 10.1 - Prob. 65ECh. 10.1 - Prob. 66ECh. 10.1 - Prob. 67ECh. 10.1 - Prob. 68ECh. 10.1 - Prob. 69ECh. 10.1 - Prob. 70ECh. 10.1 - The elliptical ceiling in Statuary Hall in the...Ch. 10.1 - Prob. 72ECh. 10.1 - Prob. 73ECh. 10.1 - Prob. 74ECh. 10.1 - Prob. 75ECh. 10.1 - Prob. 76ECh. 10.1 - Prob. 77ECh. 10.1 - Prob. 78ECh. 10.1 - Prob. 79ECh. 10.1 - Prob. 80ECh. 10.1 - Prob. 81ECh. 10.1 - 82. Write an equation for the path of each of the...Ch. 10.1 - Make Sense? In Exercises 83-86, determine whether...Ch. 10.1 - Prob. 84ECh. 10.1 - Prob. 85ECh. 10.1 - Prob. 86ECh. 10.1 - Prob. 87ECh. 10.1 - Prob. 88ECh. 10.1 - Prob. 89ECh. 10.1 - Prob. 90ECh. 10.1 - Prob. 91ECh. 10.1 - Prob. 92ECh. 10.1 - Prob. 93ECh. 10.1 - Prob. 94ECh. 10.1 - Prob. 95ECh. 10.1 - Prob. 96ECh. 10.1 - Exercises 95-97 will help you prepare for the...Ch. 10.2 - Fill in each blank so that the resulting statement...Ch. 10.2 - Prob. 2CVCCh. 10.2 - Prob. 3CVCCh. 10.2 - Prob. 4CVCCh. 10.2 - Prob. 5CVCCh. 10.2 - Prob. 6CVCCh. 10.2 - Prob. 7CVCCh. 10.2 - Prob. 8CVCCh. 10.2 - Prob. 9CVCCh. 10.2 - Prob. 10CVCCh. 10.2 - In Exercises 1-4, find the vertices and locate the...Ch. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - In Exercises 5-12, find the standard form of the...Ch. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - In Exercises 5-12, find the standard form of the...Ch. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - In Exercises 13-26, use vertices and asymptotes to...Ch. 10.2 - Prob. 17ECh. 10.2 - Prob. 18ECh. 10.2 - Prob. 19ECh. 10.2 - Prob. 20ECh. 10.2 - Prob. 21ECh. 10.2 - Prob. 22ECh. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - Prob. 25ECh. 10.2 - Prob. 26ECh. 10.2 - Prob. 27ECh. 10.2 - Prob. 28ECh. 10.2 - Prob. 29ECh. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - Prob. 37ECh. 10.2 - Prob. 38ECh. 10.2 - In Exercises 33—42, use the center, vertices, and...Ch. 10.2 - Prob. 40ECh. 10.2 - In Exercises 33—42, use the center, vertices, and...Ch. 10.2 - Prob. 42ECh. 10.2 - Prob. 43ECh. 10.2 - Prob. 44ECh. 10.2 - Prob. 45ECh. 10.2 - In Exercises -43-50, convert each equation to...Ch. 10.2 - Prob. 47ECh. 10.2 - Prob. 48ECh. 10.2 - Prob. 49ECh. 10.2 - Prob. 50ECh. 10.2 - Prob. 51ECh. 10.2 - Prob. 52ECh. 10.2 - Prob. 53ECh. 10.2 - Prob. 54ECh. 10.2 - Prob. 55ECh. 10.2 - Prob. 56ECh. 10.2 - Prob. 57ECh. 10.2 - Prob. 58ECh. 10.2 - Prob. 59ECh. 10.2 - Prob. 60ECh. 10.2 - 61. An explosion is recorded by two microphones...Ch. 10.2 - Radio lowers A and B. 200 kilometers apart, are...Ch. 10.2 - Prob. 63ECh. 10.2 - Prob. 64ECh. 10.2 - Prob. 65ECh. 10.2 - Prob. 66ECh. 10.2 - Prob. 67ECh. 10.2 - Prob. 68ECh. 10.2 - Prob. 69ECh. 10.2 - Prob. 70ECh. 10.2 - Prob. 71ECh. 10.2 - Prob. 72ECh. 10.2 - Prob. 73ECh. 10.2 - Prob. 74ECh. 10.2 - Prob. 75ECh. 10.2 - Prob. 76ECh. 10.2 - Prob. 77ECh. 10.2 - Prob. 78ECh. 10.2 - Prob. 79ECh. 10.2 - Prob. 80ECh. 10.2 - Prob. 81ECh. 10.2 - I noticed that the definition of a hyperbola...Ch. 10.2 - Prob. 83ECh. 10.2 - Prob. 84ECh. 10.2 - Prob. 85ECh. 10.2 - In Exercises 85-88, determine whether each...Ch. 10.2 - Prob. 87ECh. 10.2 - Prob. 88ECh. 10.2 - Prob. 89ECh. 10.2 - Prob. 90ECh. 10.2 - Prob. 91ECh. 10.2 - Prob. 92ECh. 10.2 - Prob. 93ECh. 10.2 - Prob. 94ECh. 10.2 - Prob. 95ECh. 10.2 - Prob. 96ECh. 10.2 - Prob. 97ECh. 10.2 - Prob. 98ECh. 10.3 - The set of all points in a plane that are...Ch. 10.3 - Prob. 2CVCCh. 10.3 - Use the graph shown to answer Exercises 2-5. If...Ch. 10.3 - Prob. 4CVCCh. 10.3 - Use the graph shown to answer Exercises 2-5. If...Ch. 10.3 - Use the graph shown lo answer Exercises 6-9.
6....Ch. 10.3 - Prob. 7CVCCh. 10.3 - Use the graph shown to answer Exercises 6-9. If...Ch. 10.3 - Use the graph shown to answer Exercises 6-9. If...Ch. 10.3 - Prob. 10CVCCh. 10.3 - In Exercises 1-4, find the focus and directrix of...Ch. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - In Exercises 17-30, find the standard form of the...Ch. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Prob. 24ECh. 10.3 - Prob. 25ECh. 10.3 - Prob. 26ECh. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 33ECh. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.3 - Prob. 37ECh. 10.3 - Prob. 38ECh. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Prob. 52ECh. 10.3 - Prob. 53ECh. 10.3 - Prob. 54ECh. 10.3 - Prob. 55ECh. 10.3 - Prob. 56ECh. 10.3 - Prob. 57ECh. 10.3 - Prob. 58ECh. 10.3 - Prob. 59ECh. 10.3 - Prob. 60ECh. 10.3 - Prob. 61ECh. 10.3 - In Exercises 57-62, use the vertex and the...Ch. 10.3 - Prob. 63ECh. 10.3 - Prob. 64ECh. 10.3 - Prob. 65ECh. 10.3 - Prob. 66ECh. 10.3 - Prob. 67ECh. 10.3 - Prob. 68ECh. 10.3 - Prob. 69ECh. 10.3 - Prob. 70ECh. 10.3 - Prob. 71ECh. 10.3 - Prob. 72ECh. 10.3 - Prob. 73ECh. 10.3 - 74. The towers of a suspension bridge are 800 feet...Ch. 10.3 - Prob. 75ECh. 10.3 - Prob. 76ECh. 10.3 - Prob. 77ECh. 10.3 - Prob. 78ECh. 10.3 - Prob. 79ECh. 10.3 - 80. Describe one similarity and one difference...Ch. 10.3 - Prob. 81ECh. 10.3 - Prob. 82ECh. 10.3 - Prob. 83ECh. 10.3 - Prob. 84ECh. 10.3 - Prob. 85ECh. 10.3 - Prob. 86ECh. 10.3 - Prob. 87ECh. 10.3 - Prob. 88ECh. 10.3 - Prob. 89ECh. 10.3 - Make Sense? In Exercises 90-93. determine whether...Ch. 10.3 - Prob. 91ECh. 10.3 - Prob. 92ECh. 10.3 - Prob. 93ECh. 10.3 - Prob. 94ECh. 10.3 - Prob. 95ECh. 10.3 - Prob. 96ECh. 10.3 - Prob. 97ECh. 10.3 - Prob. 98ECh. 10.3 - Prob. 99ECh. 10.3 - Prob. 100ECh. 10.3 - Prob. 101ECh. 10.3 - Prob. 102ECh. 10.3 - Prob. 103ECh. 10.3 - Prob. 104ECh. 10.3 - Prob. 105ECh. 10.3 - Prob. 106ECh. 10.3 - Prob. 107ECh. 10.4 - Prob. 1CVCCh. 10.4 - Prob. 2CVCCh. 10.4 - Prob. 1ECh. 10.4 - Prob. 2ECh. 10.4 - Prob. 3ECh. 10.4 - Prob. 4ECh. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - In Exercises 7-18, write the appropriate rotation...Ch. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Prob. 20ECh. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Prob. 25ECh. 10.4 - Prob. 26ECh. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Prob. 30ECh. 10.4 - Prob. 31ECh. 10.4 - Prob. 32ECh. 10.4 - Prob. 33ECh. 10.4 - Prob. 34ECh. 10.4 - Prob. 35ECh. 10.4 - In Exercises 31-36.identify each equation without...Ch. 10.4 - In Exercises 37-40,
• If the graph of the equation...Ch. 10.4 - Prob. 38ECh. 10.4 - In Exercises 37-40, If the graph of the equation...Ch. 10.4 - In Exercises 37-40. If the graph of the equation...Ch. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - Prob. 43ECh. 10.4 - Prob. 44ECh. 10.4 - Prob. 45ECh. 10.4 - Prob. 46ECh. 10.4 - Prob. 47ECh. 10.4 - Prob. 48ECh. 10.4 - Prob. 49ECh. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.4 - Prob. 54ECh. 10.4 - Prob. 55ECh. 10.4 - Prob. 56ECh. 10.4 - Prob. 57ECh. 10.4 - In Exercises 58 -59, let Ax2+Bxy+Cy2+Dx+Ey+F=0 be...Ch. 10.4 - Prob. 59ECh. 10.4 - Prob. 60ECh. 10.4 - Prob. 61ECh. 10.4 - Prob. 62ECh. 10.4 - Prob. 63ECh. 10.4 - Prob. 64ECh. 10.4 - Prob. 65ECh. 10.4 - Prob. 66ECh. 10.5 - Prob. 1CVCCh. 10.5 - Prob. 2CVCCh. 10.5 - Prob. 3CVCCh. 10.5 - Prob. 4CVCCh. 10.5 - Prob. 1ECh. 10.5 - Prob. 2ECh. 10.5 - Prob. 3ECh. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - In Exercises 21-40, eliminate the parameter t....Ch. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Prob. 47ECh. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - Prob. 50ECh. 10.5 - Prob. 51ECh. 10.5 - Prob. 52ECh. 10.5 - Prob. 53ECh. 10.5 - Prob. 54ECh. 10.5 - Prob. 55ECh. 10.5 - Prob. 56ECh. 10.5 - Prob. 57ECh. 10.5 - Prob. 58ECh. 10.5 - Prob. 59ECh. 10.5 - Prob. 60ECh. 10.5 - Prob. 61ECh. 10.5 - Prob. 62ECh. 10.5 - Prob. 63ECh. 10.5 - In Exercises 63-68, sketch the function...Ch. 10.5 - In Exercises 63-68, sketch the function...Ch. 10.5 - Prob. 66ECh. 10.5 - Prob. 67ECh. 10.5 - Prob. 68ECh. 10.5 - Prob. 69ECh. 10.5 - The path of a projectile that is launched h feet...Ch. 10.5 - Prob. 71ECh. 10.5 - Prob. 72ECh. 10.5 - What is the significance of arrows along a plane...Ch. 10.5 - Prob. 74ECh. 10.5 - Prob. 75ECh. 10.5 - Prob. 76ECh. 10.5 - Prob. 77ECh. 10.5 - Prob. 78ECh. 10.5 - Prob. 79ECh. 10.5 - Prob. 80ECh. 10.5 - Prob. 81ECh. 10.5 - Prob. 82ECh. 10.5 - In Exercises 83-84, use a graphing utility to...Ch. 10.5 - Prob. 84ECh. 10.5 - Prob. 85ECh. 10.5 - Prob. 86ECh. 10.5 - Prob. 87ECh. 10.5 - Prob. 88ECh. 10.5 - Prob. 89ECh. 10.5 - Prob. 90ECh. 10.5 - Prob. 91ECh. 10.5 - Prob. 92ECh. 10.5 - Find all zeros of f(x)=2x3+2x213x+6. (Section 3.4,...Ch. 10.5 - Prob. 94ECh. 10.5 - Prob. 95ECh. 10.5 - Prob. 96ECh. 10.5 - Prob. 97ECh. 10.5 - Prob. 98ECh. 10.5 - Prob. 99ECh. 10.6 - Prob. 1CVCCh. 10.6 - Prob. 2CVCCh. 10.6 - Fill in each blank so that the resulting statement...Ch. 10.6 - Fill in each blank so that the resulting statement...Ch. 10.6 - Fill in each blank so that the resulting statement...Ch. 10.6 - Prob. 1ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - In Exercises 21 -28 , describe a viewing...Ch. 10.6 - Halley's Cornel has an elliptical orbit with the...Ch. 10.6 - Prob. 30ECh. 10.6 - On February 20,1962, John Glenn made the first...Ch. 10.6 - On February 20, 1962, John Glenn made the first...Ch. 10.6 - Prob. 33ECh. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - Describe a strategy for graphing r=11+sin.Ch. 10.6 - You meet an astronaut and she asks you to tell her...Ch. 10.6 - Use the polar mode of a graphing utility with...Ch. 10.6 - Prob. 40ECh. 10.6 - Prob. 41ECh. 10.6 - Prob. 42ECh. 10.6 - Prob. 43ECh. 10.6 - Prob. 44ECh. 10.6 - Prob. 45ECh. 10.6 - Make Sense? In Exercises 46-49, determine whether...Ch. 10.6 - Prob. 47ECh. 10.6 - Prob. 48ECh. 10.6 - Prob. 49ECh. 10.6 - Prob. 50ECh. 10.6 - In Exercises 51-52, write a polar equation of the...Ch. 10.6 - In Exercises 51-52, write a polar equation of the...Ch. 10.6 - Prob. 53ECh. 10.6 - Prob. 54ECh. 10.6 - 55. Expand: (Section 4.3, Example 4)
Ch. 10.6 - Solve the system: { x+y=1x2+y2=25 (Section 8.4,...Ch. 10.6 - 57. Verify the identity:
...Ch. 10.6 - Two fire-lookout stations are 10 miles apart with...Ch. 10.6 - Exercises 59-61 will help you prepare for the...Ch. 10.6 - Exercises 59-61 will help you prepare for the...Ch. 10.6 - Exercises 59-61 will help you prepare for the...Ch. 10 - In Exercises 1-5, graph each ellipse. Give the...Ch. 10 - Prob. 2MCCPCh. 10 - Prob. 3MCCPCh. 10 - Prob. 4MCCPCh. 10 - Prob. 5MCCPCh. 10 - In Exercises 6-11, graph each hyperbola. Give the...Ch. 10 - In Exercises 6-11, graph each hyperbola. Give the...Ch. 10 - In Exercises 6-11, graph each hyperbola. Give the...Ch. 10 - In Exercises 6-11, graph each hyperbola. Give the...Ch. 10 - In Exercises 6-11. graph each hyperbola. Give the...Ch. 10 - In Exercises 6-11, graph each hyperbola. Give the...Ch. 10 - In Exercises 12-13 , graph each parabola. Give the...Ch. 10 - In Exercises 12-13 . graph each parabola. Give the...Ch. 10 - In Exercises 14-16, identify each equation without...Ch. 10 - In Exercises 14-16, identify each equation without...Ch. 10 - In Exercises 14-16, identify each equation without...Ch. 10 - In Exercises 17-24, graph each equation. x2+y2=4Ch. 10 - In Exercises 17-24, graph each equation.
18.
Ch. 10 - In Exercises 17-24, graph each equation.
19.
Ch. 10 - In Exercises 17-24, graph each equation.
20.
Ch. 10 - In Exercises 17-24, graph each equation.
21.
Ch. 10 - In Exercises 17-24, graph each equation.
22.
Ch. 10 - In Exercises 17-24, graph each equation....Ch. 10 - In Exercises 17-24, graph each equation....Ch. 10 - Prob. 25MCCPCh. 10 - In Exercises 25-30, find the standard form of the...Ch. 10 - Prob. 27MCCPCh. 10 - Prob. 28MCCPCh. 10 - In Exercises 25-30, find the standdpd form of the...Ch. 10 - In Exercises 25-30, find the standard form of the...Ch. 10 - A semielliptical archway over a one-way road has a...Ch. 10 - A lithotriper is used to disentegrate kidney...Ch. 10 - 33. An explosion is recorded by two forest...Ch. 10 - A domed ceiling is a parabolic surface. Ten meters...Ch. 10 - In Exercises 1-8, graph each ellipse and locate...Ch. 10 - Prob. 2RECh. 10 - In Exercises 1-8, graph each ellipse and locate...Ch. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - In Exercises 15-22, graph each hyperbula. Locate...Ch. 10 - In Exercises 15-22, graph each hyperbola. Locate...Ch. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - 25. Explain why it is not possible for a hyperbola...Ch. 10 - 26. Radio tower M2 is located 200 miles due west...Ch. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - In Exercises 27-33, find the vertex, focus, and...Ch. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - In Exercises 39 42, identify the conic represented...Ch. 10 - In Exercises 39-42, identify the conic represented...Ch. 10 - In Exercises 39-42, identify the conic represented...Ch. 10 - In Exercises 39-42. identify the conic represented...Ch. 10 - In Exercises 43 -46, identify the conic...Ch. 10 - In Exercises 43 -46, identify the conic...Ch. 10 - In Exercises 43 -46, identify the conic...Ch. 10 - In Exercises 43 -46 , identify the conic...Ch. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - In Exercises 52 -57. eliminate the parameter and...Ch. 10 - In Exercises 52 -57 . eliminate the parameter and...Ch. 10 - In Exercises 52 -57, eliminate the parameter and...Ch. 10 - In Exercises 52 -57. eliminate the parameter and...Ch. 10 - In Exercises 52 -57. eliminate the parameter and...Ch. 10 - In Exercises 52 -57. eliminate the parameter and...Ch. 10 - Find two different sets of parametric equations...Ch. 10 - 59. The path of a projectile that is launched h...Ch. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Prob. 64RECh. 10 - Prob. 65RECh. 10 - In Exercises 1-5. graph the conic section with the...Ch. 10 - Prob. 2TCh. 10 - Prob. 3TCh. 10 - Prob. 4TCh. 10 - Prob. 5TCh. 10 - In Exercises 6-8, find the standard form of the...Ch. 10 - Prob. 7TCh. 10 - In Exercises 6-8, find the standard form of the...Ch. 10 - In Exercises 6 ft, find the standard form of the...Ch. 10 - 10. An engineer is designing headlight units for...Ch. 10 - In Exercises 11-12, identify each equation without...Ch. 10 - In Exercises 11-12, identify each equation without...Ch. 10 - Prob. 13TCh. 10 - In Exercises 14 -15. eliminate the parameter and...Ch. 10 - In Exercises 14-15 eliminate the parameter and...Ch. 10 - Prob. 16TCh. 10 - Prob. 17TCh. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each equation or inequality in Exercises...Ch. 10 - Solve each system in Exercises 8-10. 8.
Ch. 10 - Solve each system in Exercises 8-10. 9. {...Ch. 10 - Solve each system in Exercises 8-10. (Use...Ch. 10 - In Exercises 11-13, graph each equation, function,...Ch. 10 - In Exercises 11-13, graph each equation, function,...Ch. 10 - In Exercises 11-13, graph each equation, function,...Ch. 10 - a. List all possible rational roots of...Ch. 10 - 15. The figure shows ihe graph of and its two...Ch. 10 - 16. If
Ch. 10 - 17. Expand using logarithmic properties. Where...Ch. 10 - 18. Write the slope-intercept form of the equation...Ch. 10 - Rent-a-Truck charges a daily rental rate for a...Ch. 10 - The local cable television company offers two...Ch. 10 - 21. Verify the identity:
Ch. 10 - Graph one complete cycle of y=2cos(2x+).Ch. 10 - Prob. 23CRECh. 10 - Solve for :sin2=sin,02.Ch. 10 - In oblique triangle ABC,A=64,B=72,anda=13.6. Solve...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Select the best statement. A. If a set of vectors includes the zero vector 0, then the set of vectors can span R^ as long as the other vectors are distinct. n B. If a set of vectors includes the zero vector 0, then the set of vectors spans R precisely when the set with 0 excluded spans Rª. ○ C. If a set of vectors includes the zero vector 0, then the set of vectors can span Rn as long as it contains n vectors. ○ D. If a set of vectors includes the zero vector 0, then there is no reasonable way to determine if the set of vectors spans Rn. E. If a set of vectors includes the zero vector 0, then the set of vectors cannot span Rn. F. none of the abovearrow_forwardWhich of the following sets of vectors are linearly independent? (Check the boxes for linearly independent sets.) ☐ A. { 7 4 3 13 -9 8 -17 7 ☐ B. 0 -8 3 ☐ C. 0 ☐ D. -5 ☐ E. 3 ☐ F. 4 THarrow_forward3 and = 5 3 ---8--8--8 Let = 3 U2 = 1 Select all of the vectors that are in the span of {u₁, u2, u3}. (Check every statement that is correct.) 3 ☐ A. The vector 3 is in the span. -1 3 ☐ B. The vector -5 75°1 is in the span. ГОЛ ☐ C. The vector 0 is in the span. 3 -4 is in the span. OD. The vector 0 3 ☐ E. All vectors in R³ are in the span. 3 F. The vector 9 -4 5 3 is in the span. 0 ☐ G. We cannot tell which vectors are i the span.arrow_forward
- (20 p) 1. Find a particular solution satisfying the given initial conditions for the third-order homogeneous linear equation given below. (See Section 5.2 in your textbook if you need a review of the subject.) y(3)+2y"-y-2y = 0; y(0) = 1, y'(0) = 2, y"(0) = 0; y₁ = e*, y2 = e¯x, y3 = e−2x (20 p) 2. Find a particular solution satisfying the given initial conditions for the second-order nonhomogeneous linear equation given below. (See Section 5.2 in your textbook if you need a review of the subject.) y"-2y-3y = 6; y(0) = 3, y'(0) = 11 yc = c₁ex + c2e³x; yp = −2 (60 p) 3. Find the general, and if possible, particular solutions of the linear systems of differential equations given below using the eigenvalue-eigenvector method. (See Section 7.3 in your textbook if you need a review of the subject.) = a) x 4x1 + x2, x2 = 6x1-x2 b) x=6x17x2, x2 = x1-2x2 c) x = 9x1+5x2, x2 = −6x1-2x2; x1(0) = 1, x2(0)=0arrow_forwardFind the perimeter and areaarrow_forwardAssume {u1, U2, us} spans R³. Select the best statement. A. {U1, U2, us, u4} spans R³ unless u is the zero vector. B. {U1, U2, us, u4} always spans R³. C. {U1, U2, us, u4} spans R³ unless u is a scalar multiple of another vector in the set. D. We do not have sufficient information to determine if {u₁, u2, 43, 114} spans R³. OE. {U1, U2, 3, 4} never spans R³. F. none of the abovearrow_forward
- Assume {u1, U2, 13, 14} spans R³. Select the best statement. A. {U1, U2, u3} never spans R³ since it is a proper subset of a spanning set. B. {U1, U2, u3} spans R³ unless one of the vectors is the zero vector. C. {u1, U2, us} spans R³ unless one of the vectors is a scalar multiple of another vector in the set. D. {U1, U2, us} always spans R³. E. {U1, U2, u3} may, but does not have to, span R³. F. none of the abovearrow_forwardLet H = span {u, v}. For each of the following sets of vectors determine whether H is a line or a plane. Select an Answer u = 3 1. -10 8-8 -2 ,v= 5 Select an Answer -2 u = 3 4 2. + 9 ,v= 6arrow_forwardSolve for the matrix X: X (2 7³) x + ( 2 ) - (112) 6 14 8arrow_forward
- 5. Solve for the matrix X. (Hint: we can solve AX -1 = B whenever A is invertible) 2 3 0 Χ 2 = 3 1arrow_forwardWrite p(x) = 6+11x+6x² as a linear combination of ƒ (x) = 2+x+4x² and g(x) = 1−x+3x² and h(x)=3+2x+5x²arrow_forward3. Let M = (a) - (b) 2 −1 1 -1 2 7 4 -22 Find a basis for Col(M). Find a basis for Null(M).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Evaluating Indefinite Integrals; Author: Professor Dave Explains;https://www.youtube.com/watch?v=-xHA2RjVkwY;License: Standard YouTube License, CC-BY
Calculus - Lesson 16 | Indefinite and Definite Integrals | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=bMnMzNKL9Ks;License: Standard YouTube License, CC-BY