Mathematics for Elementary Teachers with Activities (5th Edition)

5th Edition

ISBN: 9780134392790

Author: Beckmann, Sybilla

Publisher: PEARSON

See similar textbooks

Concept explainers

Optimization

Optimization comes from the same root as "optimal". "Optimal" means the highest. When you do the optimization process, that is when you are "making it best" to maximize everything and to achieve optimal results, a set of parameters is the base for the se…

Integration

Integration means to sum the things. In mathematics, it is the branch of Calculus which is used to find the area under the curve. The operation subtraction is the inverse of addition, division is the inverse of multiplication. In the same way, integratio…

Application of Integration

In mathematics, the process of integration is used to compute complex area related problems. With the application of integration, solving area related problems, whether they are a curve, or a curve between lines, can be done easily.

Volume

In mathematics, we describe the term volume as a quantity that can express the total space that an object occupies at any point in time. Usually, volumes can only be calculated for 3-dimensional objects. By 3-dimensional or 3D objects, we mean objects th…

Area

Area refers to the amount of space a figure encloses and the number of square units that cover a shape. It is two-dimensional and is measured in square units.

Videos

Textbook Question

Chapter 10.2, Problem 8P

A convex mirror Is a minor that curves out, so that the normal lines on the reflective side of the mirror point away from each other, as shown at the top of Flgure 10.58 . Convex mirrors are often used as side-view mirrors on cars and trucks. This problem will help you see why convex mirrors are useful for this purpose. Figure 10.56 shows a bird's-eye view of a cross-section of a convex mirror. a cross-section of a flat mirror. and eyes looking into these minors. Draw a copy of these mirrors and the eyes looking into them. Use the laws of reflection to help you compare how much of the surrounding environment each eye can see, looking into its mirror.

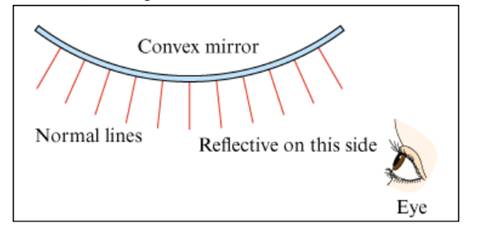
Chapter 10.2, Problem 8P, A convex mirror Is a minor that curves out, so that the normal lines on the reflective side of the , example 1
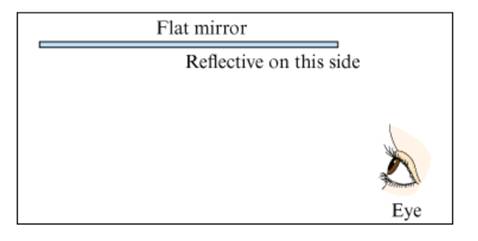
Figure 10.56A convex mirror and a flat mirror

Now explain why Convex mirror are often used as side −view mirrors on car and trucks .

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 10.2, Problem 7P

Chapter 10.2, Problem 9P

Chapter 10 Solutions

Mathematics for Elementary Teachers with Activities (5th Edition)

Ch. 10.1 - Tiffany says that the angle at A in Figure 10.29...Ch. 10.1 - Given that the indicated lines in Figure 10.30(a)...Ch. 10.1 - Given that the indicated lines in Figure 10.30 (b)...Ch. 10.1 - Ch. 10.1 - Ed the robot is standing at point A and will walk...Ch. 10.1 - Draw a map that shows the following route leading...Ch. 10.1 - In your own words, give a clear, logical...Ch. 10.1 - Figure 10.33 shows a rectangle subdivided into...Ch. 10.1 - Given that the lines In Flgure 10.34 marked with...Ch. 10.1 - Determine the sum a+b+c+d+e+f of the angles in the...

Ch. 10.1 - Given that the lines marked with arrows in Flgure...Ch. 10.1 - Determine the sum of the angles at the star...Ch. 10.2 - Figure 10.46 9 depicts sun rays traveling toward 3...Ch. 10.2 - Figure. 10.48 shows a cross-section of Joey's toy...Ch. 10.2 - Figure. 10.49 shows a sketch of a room that has a...Ch. 10.2 - Many people mistakenly believe that the seasons...Ch. 10.2 - Refer to Figure 10.50 , 10.51 , 10.52 , and 10.53...Ch. 10.2 - 'Department store dressing rooms often have large...Ch. 10.2 - 'A concave mirror is a mirror that curves In, like...Ch. 10.2 - A convex mirror Is a minor that curves out, so...Ch. 10.2 - A convex mirror is a mirror that curves out, so...Ch. 10.3 - Smallville Is 7 miles south of Gotham. will is 8...Ch. 10.3 - A new mall is to be built to serve the towns of...Ch. 10.3 - A radio beacon indicates thata certain dolphin is...Ch. 10.3 - A new Giant Superstore is being planned somewhere...Ch. 10.3 - Part 1 of Class Actlvlty 10O on circle designs...Ch. 10.4 - Students sometimes get confused about the...Ch. 10.4 - Draw a Venn diagram or other clear diagram showing...Ch. 10.4 - Draw a Venn diagram or other clear diagram that...Ch. 10.4 - a. Describe how four children could use 4 pieces...Ch. 10.4 - Figure 10.85 shows a method for constructing...Ch. 10.4 - a. Fold and cut paper to make an isosceles...Ch. 10.4 - Draw a line segment AB that is 4 inches long. Now...Ch. 10.4 - a. Use a ruler and compass to help you draw a...Ch. 10.4 - Is there a triangle that has one side of length 4...Ch. 10.4 - Create two different rhombuses, both of which have...Ch. 10.4 - Prob. 11P Ch. 10.4 - In a paragraph, discuss how the detinition of...Ch. 10.4 - Give instructions telling Robot Rob how to move...Ch. 10.4 - Give instructions telling Automaton Annie how to...Ch. 10.4 - a. Flgure 10.87 shows 3 pairs of parallel line...Ch. 10.4 - a. Given a parallelogram with angles a, b, c. and...Ch. 10.4 - What is wrong with the diagram for the problem In...Ch. 10.4 - Given a right triangle that has angles a, b, and...Ch. 10.4 - Use the idea of walking and turning around a shape...Ch. 10.4 - a. Determine the angles in a regular pentagon....

Additional Math Textbook Solutions

Find more solutions based on key concepts

1. How much money is Joe earning when he’s 30?

Pathways to Math Literacy (Loose Leaf)

Fill in each blank with the correct response. 1. For any value of x, the point lies on the ____ -axis.

Mathematical Ideas (13th Edition) - Standalone book

Given estimates Kij of the entries of K and estimates 1 and 2 of the eigenvalues of K, show how to obtain an es...

Differential Equations: An Introduction to Modern Methods and Applications

Set up and solve Exercises 23–29 by the simplex method. 26. Income A baker has 150 units of flour, 90 of sugar,...

Finite Mathematics (11th Edition)

CHECK POINT I Consider the six jokes about books by Groucho Marx. Bob Blitzer. Steven Wright, HennyYoungman. Je...

Thinking Mathematically (6th Edition)

For Exercises 13–18, write the negation of the statement. 13. The cell phone is out of juice.

Math in Our World

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.

Solution Summary: The author explains that convex mirrors are often used as side view mirror on cars and trucks as it enables to see wide area of the road behind them.

Concept explainers

Videos

Want to see the full answer?

Chapter 10 Solutions

Additional Math Textbook Solutions