
Concept explainers
(a)
To list:the possible sums that result from rolling two six-sided dice.
(a)
Answer to Problem 23E
The possible sums are: 2,3,4,5,6,7,8,9,10,11,12 .
Explanation of Solution
Given:
| A | B | C | |
| 1 | First die | Second die | sum |
| 2 | 4 | 6 | 10 |
| 3 | 3 | 5 | 9 |
| 4 | 1 | 8 | 7 |
Calculation:
A probability experiment is an action, or trial that has varying results. The possible result of a probability experiment is known as outcomes. The set of all possible outcomes is called samplespace. The sample space for rolling two six sided dice are as follows:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)
Studying the outcomes, the possible sums that result from rolling two six sided dice are as follows:
2,3,4,5,6,7,8,9,10,11,12
Therefore, the answers are: 2,3,4,5,6,7,8,9,10,11,12 .
Conclusion:
Therefore, the possible sums are: 2,3,4,5,6,7,8,9,10,11,12 .
(b)
To find: the theoretical probability of rolling each sum.
(b)
Answer to Problem 23E
| Sum | probabilities | sum | probabilities |
| 2 | 0.028 | 8 | 0.1389 |
| 3 | 0.056 | 9 | 0.1111 |
| 4 | 0.0833 | 10 | 0.0833 |
| 5 | 0.1111 | 11 | 0.0556 |
| 6 | 0.1389 | 12 | 0.0278 |
| 7 | 0.1667 |
Explanation of Solution
Calculation:
There are 36 outcomes and outcomes for a specified event are called favorable outcomes. Whenall outcomes are equally likely, the theoretical probability is described as the ratio of number of favorable outcomes to total number of outcomes. Therefore, the required probability is asfollows:
Equivalently, compute the remaining probabilities. The following tale illustrates the probabilities of remaining sums.
| Sum | probabilities | sum | probabilities |
| 2 | 0.028 | 8 | 0.1389 |
| 3 | 0.056 | 9 | 0.1111 |
| 4 | 0.0833 | 10 | 0.0833 |
| 5 | 0.1111 | 11 | 0.0556 |
| 6 | 0.1389 | 12 | 0.0278 |
| 7 | 0.1667 |
Table illustrates the probabilities of rolling each sum in the second column.
Conclusion:
Therefore, the table illustrates the probabilities of rolling each sum in the second column.
| Sum | probabilities | sum | probabilities |
| 2 | 0.028 | 8 | 0.1389 |
| 3 | 0.056 | 9 | 0.1111 |
| 4 | 0.0833 | 10 | 0.0833 |
| 5 | 0.1111 | 11 | 0.0556 |
| 6 | 0.1389 | 12 | 0.0278 |
| 7 | 0.1667 |
(c)
To compare: the experimental probabilities of rolling each sum with the theoretical probabilities.
(c)
Answer to Problem 23E
The results show that both are close but not exactly equal.
Explanation of Solution
Calculation:
The experimental probability is the ratio of number of successes to number of trials. Userandom number generator to generate 50 numbers each ranging from 1 to 6 for two dices.
Calculate the sum. Then compute the experimental probability of each sum.
The following screen shot illustrates the probabilities of sums for first 24 trials.
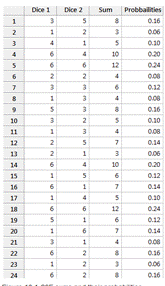
Compare both experimental and theoretical probabilities.
The results show that both are closebut not exactly equal.
Conclusion:
The results show that both are close but not exactly equal.
Chapter 10 Solutions
Big Ideas Math A Bridge To Success Algebra 2: Student Edition 2015
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





