Chapter 10.1, Problem 13PSB

To determine

To prove: Circle $A$ is congruence to circle $B$ if $DE\parallel FC,\angle ADE=\angle FCB\text{ and }DE\cong FC.$

Answer to Problem 13PSB

Circle $A$ =circle $B$ .

Explanation of Solution

Given:

  

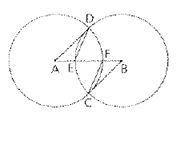
Intersecting circles $A\text{ and }B$ .

  $\begin{array}{l}DE\parallel FC.\\ \angle ADE=\angle FCB.\\ DE=FC.\end{array}$

Concept used:

Parallel lines make alternate interior angles congruent.

Supplements of congruent angle are congruent.

congruent parts of congruent triangles are congruent and congruent circle have congruent radii.

Two triangles are said to be congruent if all the three sides and three angles are same.

Condition of congruence triangle:

Side angle side $\left(SAS\right)$ : two side and one angle of one triangle is equivalent another triangle.

Side-side-side $\left(SSS\right)$ : all three side of the one triangle is equivalent to another triangle.

Angle side angle $\left(ASA\right)$ : two angle and side included between the angles of one triangle is equivalent to another two angle and side included between the angles of triangle.

Angle-angle side $\left(AAS\right)$:

two angle and non-included side between the angles of one triangle is equivalent to another two angle and non-included side between the angles of triangle.

Right angle hypotenuse side $\left(RHS\right)$: Hypotenuse and side of a right-angled triangle is equivalent to the hypotenuse and side of the second right angled triangle.

Calculation:

According to the given:

Intersecting circles $A\text{ and }B$ .

  $\begin{array}{l}DE\parallel FC.\\ \angle ADE=\angle FCB.\\ DE=FC.\end{array}$

Parallel lines make alternate interior angles congruent:

Angle $DEF=CFE$ .

Supplements of congruent angle are congruent.

Angle $DEA=CFB$ .

From angle side angle $\left(ASA\right)$ rule:

  $\left(DEF=CFE,DE=FC,DEA=CFB\right)$ .

Therefore, the triangle $\Delta DEA=\Delta CFB$ .

Since, congruent parts of congruent triangles are congruent and congruent circle have congruent radii.

Hence, circle $A$ =circle $B$ .