Chapter 10, Problem 8CR

(a)

To determine

To find: The 90% confidence interval for $p_1-p_2$.

Answer to Problem 8CR

Solution:

The 90% confidence interval for the difference of two means is $-0.2027<(p_1-p_2)<0.1823$.

Explanation of Solution

Calculation:

Let $p_1$ be the population probability of success of first experiment and $p_2$ be the proportion probability of success of second experiment.

Let $n_1=30,r_1=16,n_2=46,r_2=25$

$\begin{array}{c}{\widehat{p}}_1=\frac{r_1}{n_1}=\frac{16}{30}\\ {\widehat{p}}_1\approx 0.5333\\ \\ {\widehat{q}}_1=1-{\widehat{p}}_1\\ {\widehat{q}}_1=1-0.5333\\ {\widehat{q}}_1=0.4667\\ \\ {\widehat{p}}_2=\frac{r_2}{n_2}=\frac{25}{46}\\ {\widehat{p}}_2\approx 0.5435\\ \\ {\widehat{q}}_2=1-{\widehat{p}}_2\\ {\widehat{q}}_2=1-0.5435\\ {\widehat{q}}_2=0.4565\end{array}$

$n_1{\widehat{p}}_1=16,n_1{\widehat{q}}_1=14,n_2{\widehat{p}}_2=25,n_2{\widehat{q}}_2=21$

Since all $n_1{\widehat{p}}_1,n_1{\widehat{q}}_1,n_2{\widehat{p}}_2,n_2{\widehat{q}}_2$ are greater than 5, hence we can use the normal distribution to the approximate the ${\widehat{p}}_1-{\widehat{p}}_2$ distribution.

The critical z-value for a two-tailed area of 0.10 is 1.645.

The difference of two proportions is

$\begin{array}{c}({\widehat{p}}_1-{\widehat{p}}_2)=0.5333-0.5435\\ ({\widehat{p}}_1-{\widehat{p}}_2)=-0.0102\end{array}$

Now, the margin of error is computed as follows:

$\begin{array}{l}E=z_c\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\\ E=1.645\sqrt{\frac{0.5333(1-0.5333)}{30}+\frac{0.5435(1-0.5435)}{46}}\\ E=0.19247\\ E\approx 0.1925\end{array}$

Now the confidence interval for the difference of two means;

$\begin{array}{l}({\widehat{p}}_1-{\widehat{p}}_2)-E<(p_1-p_2)<({\widehat{p}}_1-{\widehat{p}}_2)+E\\ -0.0102-0.1925<(p_1-p_2)<-0.0102+0.1925\\ -0.2027<(p_1-p_2)<0.1823\end{array}$

The 90% confidence interval for the difference of two proportions is $-0.2027<(p_1-p_2)<0.1823$.

(b)

To determine

To explain: The meaning of confidence interval in the context of the problem.

Explanation of Solution

Since the 90% confidence interval - 0.2027 to 0.1823 contains both positive and negative value, hence we cannot say that $p_1-p_2\ne 0$ or $p_1\ne p_2$. Thus, at the 90% confidence level, we cannot conclude that there is difference in the proportion of accurate responses from face to face interview compared with telephone interview.

(c)

(i)

To determine

The level of significance and state the null and alternative hypotheses.

Answer to Problem 8CR

Solution: The level of significance is 0.05. $H_0:p_1=p_2$ and $H_1:p_1\ne p_2$.

Explanation of Solution

The level of significance, $\alpha =0.05$.

The null hypothesis for testing is defined as,

$H_0:p_1=p_2$

The alternative hypothesis is defined as,

$H_1:p_1\ne p_2$

(ii)

To determine

The sampling distribution to be used and explain the assumptions and also find the value of the test statistics.

Answer to Problem 8CR

Solution: The normal distribution is used in this study. Thetest statistic for the sample is z = - 0.09.

Explanation of Solution

Calculation:

We have $n_1=30,r_1=16,n_2=46,r_2=25$

$n_1{\widehat{p}}_1=16,n_1{\widehat{q}}_1=14,n_2{\widehat{p}}_2=25,n_2{\widehat{q}}_2=21$

Since all $n_1{\widehat{p}}_1,n_1{\widehat{q}}_1,n_2{\widehat{p}}_2,n_2{\widehat{q}}_2$ are greater than 5, hence we can use the normal distribution to the approximate the ${\widehat{p}}_1-{\widehat{p}}_2$ distribution.

The pooled estimates for $\overline{p}\text{and}\overline{q}$ are:

$\begin{array}{l}\overline{p}=\frac{r_1+r_2}{n_1+n_2}=\frac{16+25}{30+46}\\ \overline{p}=0.5395\\ \overline{q}=1-\overline{p}\\ \overline{q}=1-0.5395\\ \overline{q}=0.4605\end{array}$

The difference of two proportions is

$\begin{array}{c}({\widehat{p}}_1-{\widehat{p}}_2)=0.5333-0.5435\\ ({\widehat{p}}_1-{\widehat{p}}_2)=-0.0102\end{array}$

The sample test statistic z is given as:-

$\begin{array}{l}z=\frac{{\widehat{p}}_1-{\widehat{p}}_2}{\sqrt{\frac{\overline{p}\overline{q}}{n_1}+\frac{\overline{p}\overline{q}}{n_2}}}\\ z=\frac{-0.0102}{\sqrt{\frac{(0.5395)(0.4605)}{30}+\frac{(0.5395)(0.4605)}{46}}}\\ z=-0.0872\\ z\approx -0.09\end{array}$

(iii)

To determine

To find: The P-value of the sample statistic and sketch the sampling distribution and show the area corresponding to the P-value.

Answer to Problem 8CR

Solution: The P-value of sample statistic is 0.9362.

Explanation of Solution

Graph:

The given hypothesis test is two tailed.

$\begin{array}{l}P-\text{value =}P(z<-0.09)\text{+}P\left(z>0.09\right)\\ P-\text{value =2}P(z<-0.09)\end{array}$

By using table 4 from Appendix

$\begin{array}{l}P-\text{value =2(0}\text{.4681)}\\ P-\text{value =0}\text{.9362}\end{array}$

Graph:

To draw the required graphs using the Minitab, follow the below instructions:

Step 1: Go to the Minitab software.

Step 2: Go to Graph > Probability distribution plot > View probability.

Step 3: Select ‘Normal’, enter Mean = 0 and standard deviation =1.

Step 4: Click on the Shaded area > X value.

Step 5: Enter X-value as -0.09 and select ‘Two tail’.

Step 6: Click on OK.

The obtained distribution graph is:

$\begin{array}{l}P-\text{value =2(0}\text{.4641)}\\ P-\text{value =}0.9362\end{array}$

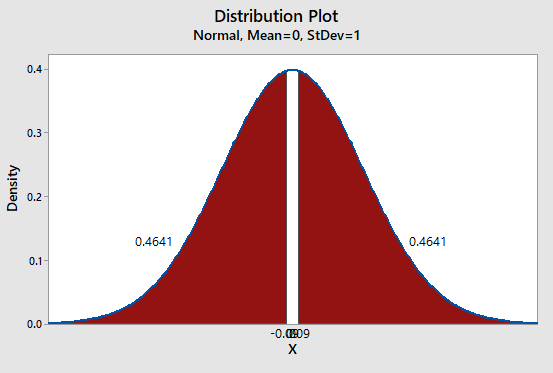
(iv)

To determine

Whether we reject or fail to reject the null hypothesis and whether the data is statistically significant for a level of significance of 0.05.

Answer to Problem 8CR

Solution: The P-value $>\alpha$, hence we failed to reject $H_0$. The data is not statistically significant for a level of significance of 0.05.

Explanation of Solution

The P-value (0.9362) is greater than the level of significance ($\alpha$) of 0.05. Therefore we failed to reject the null hypothesis $H_0$ i.e. the P-value is not statistically significant.

(v)

To determine

The interpretation for the conclusion.

Answer to Problem 8CR

Solution: There is not enough evidence to conclude that there is difference in the proportion of accurate responses from face to face interview compared with telephone interview.

Explanation of Solution

The P-value (0.9362) is greater than the level of significance ($\alpha$) of 0.05. Therefore we failed to reject the null hypothesis $H_0$ i.e. the P-value is not statistically significant.

There is not enough evidence to conclude that there is difference in the proportion of accurate responses from face to face interview compared with telephone interview.