Chapter 10, Problem 10.11QAP

Interpretation Introduction

(a)

Interpretation:

The least square analysis needs to be performed to determine the intercept, slopeand regression statistics, including the standard deviation about regression.

Concept introduction:

The least square analysis is defined as the method in which the final answer for the set of data points is calculated by the minimizing the summation of residue of set of data point from the given curve.

The equation for straight line is represented as follows:

$y=mx+c$

${\sigma }_x=\sqrt{{(\frac{\partial x}{\partial m})}^2{({\sigma }_m)}^2+{(\frac{\partial x}{\partial c})}^2{({\sigma }_c)}^2}$

Answer to Problem 10.11QAP

To satisfy the equation $y=mx+c$ from the data points,

$\begin{array}{l}m=2752.72\\ c=12590.6\\ {\sigma }_m=30.8\\ {\sigma }_c=176.31\end{array}$

Explanation of Solution

Least Square Analysis

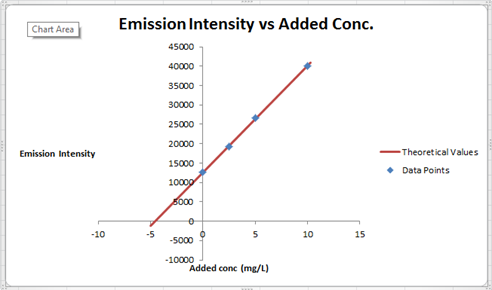
The summary of calculation is as follows.

Added Au	Emission Intensity (y)
0	12568
2.5	19324
5	26622
10	40021
m	c	2752.72	12590.6
sm	sb	30.7796445	176.3126
r2	sy	0.99975001	227.6185

Here, the sigma values focus on the errors present in the parameter.

So far, we have filled $y=mx+c$ to the data points. We have,

$\begin{array}{l}m=2752.72\\ c=12590.6\\ {\sigma }_m=30.8\\ {\sigma }_c=176.31\end{array}$

Now, we must determine the concentration of gold and its uncertainty. The concentration of gold is x. intercept of the graph, because that is the point at which the gold is absence so the difference between that and the zero added point must be the gold concentration in sample.

$y=mx+c$

$\Rightarrow x=\frac{y-c}{m}=\frac{0-12590.6}{2752.72}=-4.57mg/L$

Now, x is a function of c and m. Thus, the uncertainty in them will be propagated to x as well. We have the following since m and c are independent.

x = x(m,c)

${\sigma }_x=\sqrt{{(\frac{\partial x}{\partial m})}^2{({\sigma }_m)}^2+{(\frac{\partial x}{\partial c})}^2{({\sigma }_c)}^2}$

By propagation of uncertainty,

$\begin{array}{l}\frac{\partial x}{\partial m}=\frac{-(y-c)}{m^2}=1.66\times {10}^{-3}\\ \frac{\partial x}{\partial c}=\frac{-1}{m}=\frac{-1}{2752.72}=-3.63\times {10}^{-4}\\ {\sigma }_x=\sqrt{{(1.66\times {10}^{-3})}^2\times 30.8\times 30.8+{(-3.63\times {10}^{-4})}^2\times 176.3\times 176.3}\\ {\sigma }_x=0.082\end{array}$

This is, however, the standard error. Assuming the distribution of value to be normal about the value of x, this value would give an interval of 63.5% probability. However, if we want a 95% probability interval, we will have to multiply the error in x by 1.96.

Interpretation Introduction

(b)

Interpretation:

The concentration of gold in the sample solution in mg/L needs to be determined using the calculated values.

Concept introduction:

The least square analysis is defined as the method in which the final answer for the set of data points is calculated by the minimizing the summation of residue of set of data point from the given curve.

The equation for straight line is represented as follows:

$y=mx+c$

${\sigma }_x=\sqrt{{(\frac{\partial x}{\partial m})}^2{({\sigma }_m)}^2+{(\frac{\partial x}{\partial c})}^2{({\sigma }_c)}^2}$

Answer to Problem 10.11QAP

Concentration of gold in sample = $4.57\pm 0.082mg/L$ with 3.2% certainty.

Explanation of Solution

Least Square Analysis

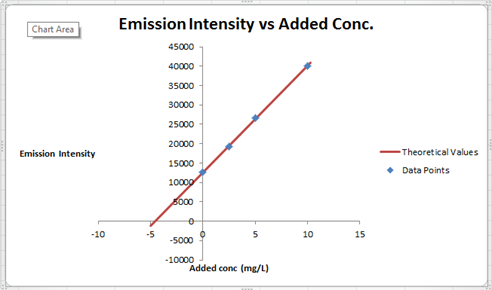
The summary of calculation is as follows.

Added Au	Emission Intensity (y)
0	12568
2.5	19324
5	26622
10	40021
m	c	2752.72	12590.6
sm	sb	30.7796445	176.3126
r2	sy	0.99975001	227.6185

Here, the sigma values focus on the errors present in the parameter.

So far, we have filled $y=mx+c$ to the data points. We have,

$\begin{array}{l}m=2752.72\\ c=12590.6\\ {\sigma }_m=30.8\\ {\sigma }_c=176.31\end{array}$

Now, we must determine the concentration of gold and its uncertainty. The concentration of gold is x. intercept of the graph, because that is the point at which the gold is absence so the difference between that and the zero added point must be the gold concentration in sample.

$y=mx+c$

$\Rightarrow x=\frac{y-c}{m}=\frac{0-12590.6}{2752.72}=-4.57mg/L$

Now, x is a function of c and m. Thus, the uncertainty in them will be propagated to x as well. We have the following since m and c are independent.

x = x(m,c)

${\sigma }_x=\sqrt{{(\frac{\partial x}{\partial m})}^2{({\sigma }_m)}^2+{(\frac{\partial x}{\partial c})}^2{({\sigma }_c)}^2}$

By propagation of uncertainty,

$\begin{array}{l}\frac{\partial x}{\partial m}=\frac{-(y-c)}{m^2}=1.66\times {10}^{-3}\\ \frac{\partial x}{\partial c}=\frac{-1}{m}=\frac{-1}{2752.72}=-3.63\times {10}^{-4}\\ {\sigma }_x=\sqrt{{(1.66\times {10}^{-3})}^2\times 30.8\times 30.8+{(-3.63\times {10}^{-4})}^2\times 176.3\times 176.3}\\ {\sigma }_x=0.082\end{array}$

This is however, the standard error. Assuming the distribution of value to be normal about the value of x, this value would give an interval of 63.5% probability. However, if we want a 95% probability interval, we will have to multiply the error in x by 1.96.

Concentration of gold in sample = $4.57\pm 0.082mg/L$ with 3.2% certainty.

Interpretation Introduction

(c)

Interpretation:

The concentration of gold in the sample is 8.51 mg/L needs to be determined and the hypothesis that the results equals the 95% confidence level needs to be tested.

Concept introduction:

The least square analysis is defined as the method in which the final answer for the set of data points is calculated by the minimizing the summation of residue of set of data point from the given curve.

The equation for straight line is represented as follows:

$y=mx+c$

${\sigma }_x=\sqrt{{(\frac{\partial x}{\partial m})}^2{({\sigma }_m)}^2+{(\frac{\partial x}{\partial c})}^2{({\sigma }_c)}^2}$

Answer to Problem 10.11QAP

Considering a confidence interval of 95% we have concentration of $4.57\pm 0.16mg/L$. Thus the maximum value it can take is 4.73 mg/L. The value of 8.51 mg/L exceeds this value. The result is not equal to this value.

Explanation of Solution

Least Square Analysis

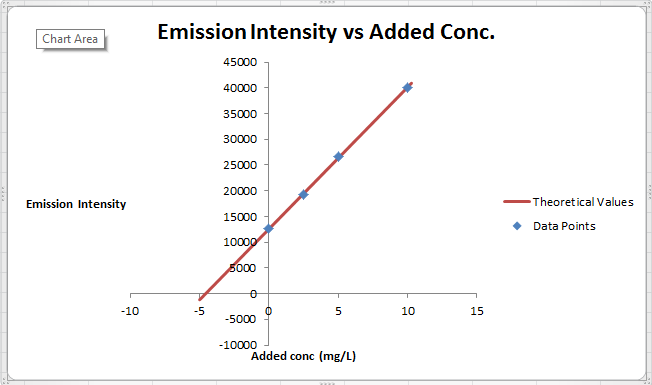
The summary of calculation is as follows.

Added Au	Emission Intensity (y)
0	12568
2.5	19324
5	26622
10	40021
m	c	2752.72	12590.6
sm	sb	30.7796445	176.3126
r2	sy	0.99975001	227.6185

Here, the sigma values focus on the errors present in the parameter.

So far, we have filled $y=mx+c$ to the data points. We have,

$\begin{array}{l}m=2752.72\\ c=12590.6\\ {\sigma }_m=30.8\\ {\sigma }_c=176.31\end{array}$

Now, we must determine the concentration of gold and its uncertainty. The concentration of gold is x. intercept of the graph, because that is the point at which the gold is absence so the difference between that and the zero added point must be the gold concentration in sample.

$y=mx+c$

$\Rightarrow x=\frac{y-c}{m}=\frac{0-12590.6}{2752.72}=-4.57mg/L$

Now, x is a function of c and m. Thus, the uncertainty in them will be propagated to x as well. We have the following since m and c are independent.

x = x(m,c)

${\sigma }_x=\sqrt{{(\frac{\partial x}{\partial m})}^2{({\sigma }_m)}^2+{(\frac{\partial x}{\partial c})}^2{({\sigma }_c)}^2}$

By propagation of uncertainty,

$\begin{array}{l}\frac{\partial x}{\partial m}=\frac{-(y-c)}{m^2}=1.66\times {10}^{-3}\\ \frac{\partial x}{\partial c}=\frac{-1}{m}=\frac{-1}{2752.72}=-3.63\times {10}^{-4}\\ {\sigma }_x=\sqrt{{(1.66\times {10}^{-3})}^2\times 30.8\times 30.8+{(-3.63\times {10}^{-4})}^2\times 176.3\times 176.3}\\ {\sigma }_x=0.082\end{array}$

This is however, the standard error. Assuming the distribution of value to be normal about the value of x, this value would give an interval of 63.5% probability. However, if we want a 95% probability interval, we will have to multiply the error in x by 1.96.

Considering a confidence interval of 95% we have concentration of $4.57\pm 0.16mg/L$. Thus, the maximum value it can take is 4.73 mg/L. The value of 8.51 mg/L exceeds this value. The result is not equal to this value.