
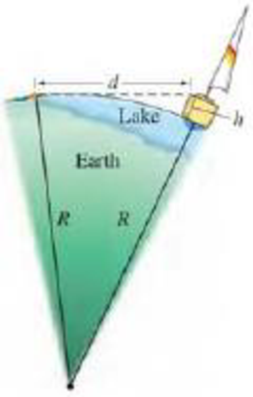
(III) Many sailboats are moored at a marina 4.4 km away on the opposite side of a lake. You stare at one of the sailboats because, when you are lying flat at the water’s edge, you can just see its duck but none of the side of the sailboat. You then go to that sailboat on the other side of the lake and measure that the deck is 1.5 m above the level of the water. Using Fig. 1–12, where h = 1.5 m, estimate the radius R of the Earth.
FIGURE 1–12 Problem 33. You see a sailboat across a lake (not to scale). R is the radius of the Earth. You are a distance d = 4.4 km from the sailboat when you can see only its deck and not its side. Because of the curvature of the Earth, the water “bugles out” between you and the boat.
Trending nowThis is a popular solution!

Chapter 1 Solutions
Physics for Scientists and Engineers with Modern Physics
Additional Science Textbook Solutions
Modern Physics
Conceptual Physical Science (6th Edition)
University Physics Volume 2
Physics (5th Edition)
Introduction to Electrodynamics
Essential University Physics: Volume 2 (3rd Edition)
- A surveyor measures the distance across a straight river by the following method (Fig. P3.7). Starting directly across from a tree on the opposite bank, she walks d = 100 m along the riverbank to establish a baseline. Then she sights across to the tree. The angle from her baseline to the tree is = 35.0. How wide is the river?arrow_forwardOne liter of oil is spilled onto a smooth lake. If the oil spreads out uniformly until it makes an oil slick just one molecule thick, with adjacent molecules justtouching, estimate the diameter of the oil slick. Assume the oil molecules have a diameter of 2 x 10–10 m.arrow_forwardHold a pencil in front of your eye at a position where its blunt end just blocks out the Moon (Fig. 1–19). Make appropriate measurements to estimate the diameter of the Moon, given that the Earth-Moon distance is 3.8 × 10° km. FIGURE 1-19 Problem 48. How big is the Moon?arrow_forward
- (b) Sphericals x=r sine coso y=r sine sino z=r cose Consider spherical coordinates as defined by their relationships to the Cartesian coordinates: x =r sin 8 cos p X2 =r sin 0 cos X3 =r cos 0 r2 = [xỉ + x3 + x e = tan-(x? + x3)x3 $ = tan-(x2/x1) orarrow_forwardIron has a density of 7.87 g/cm3, and the mass of an iron atom is 9.27 * 10-26 kg. If the atoms are spherical and tightly packed, (a) what is the volume of an iron atom and (b) what is the distance between the centers of adjacent atoms?arrow_forwardJim stands beside a wide river and wonders how wide it is. He spots a large rock on the bank directly across from him. He then walks upstream 65 strides and judges that the angle between him and the rock, which he can still see, is now at an angle of 30° downstream (Fig. 1–20). Jim measures his stride 30° ! to be about 0.8 m long. Estimate the width of the river. FIGURE 1-20 Problem 54. 65 Stridesarrow_forward
- (III) The smallest meaningful measure of length is called the Planck length, and is defined in terms of three fundamental constants in nature: the speed of light c the gravitational constant G = 6.67 × 10-11 m³/kg•s², and Planck's constant h = 6.63 × 10-34 kg·m²/s. The Planck length {p is given by the following combination of these three constants: 3.00 × 10° m/s, Gh lp Show that the dimensions of lp are length [L], and find the order of magnitude of lp. [Recent theories (Chapters 32 and 33) suggest that the smallest particles (quarks, leptons) are “strings" with lengths on the order of the Planck length, 10-35 m. These theories also suggest that the “Big Bang," with which the universe is believed to have begun, started from an initial size on the order of the Planck length.]arrow_forward(II) A typical atom has a diameter of about 1.0 x 10–10 m. (a) What is this in inches? (b) Approximately how many atoms are along a 1.0-cm line, assuming they just touch?arrow_forward(II) Determine the conversion factor between (a) km/h and mi/h,(b) m/s and ft/s,(c) km/h and m/s.arrow_forward
- 3 and 0 < 0 < 7' find the other five trigonometric of 0 (4)If tan0 = -arrow_forward(a) Calculate the approximate number of atoms in a single sheet of 0.01 lb paper. Note that a single carbon atom is about 2×10-26 kg in mass and 1 lb is approximately 4.448 N. (b) Estimate to order of magnitude the total mass of paper used by a typical class throughout a semester.arrow_forwardGiven that 1in = 2.54 cm, then 10in is equal to how many cm?arrow_forward
 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning

