
Write the fractional part that each length, A through F, represents of the total shown on the scale in Figure 1-3.
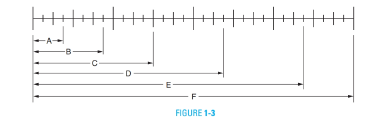
A = .
B = .
C = .
D = .
E = .
F = .
Evaluate the fractional part length of A, B, C, D, E and F.
Answer to Problem 1A
The fractional part length of A, B, C, D, E and F are
Explanation of Solution
Given:
All the dimensions are shown in below Fig:
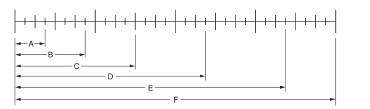
Concept used:
Fraction of the each part can determine with given expression.
Here, length of each part is
Calculation:
From below Fig:
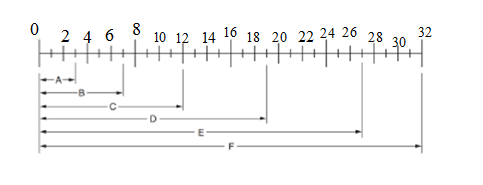
Fraction A is calculated as:
Substitute
Fraction B is calculated as:
Substitute
Fraction C is calculated as:
Substitute
Fraction D is calculated as:
Substitute
Fraction E is calculated as:
Substitute
Fraction F is calculated as:
Substitute
Thus, the fractional part length of A, B, C, D, E and F are
Conclusion:
The fractional part length of A, B, C, D, E and F are
Want to see more full solutions like this?
Chapter 1 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
- Consider a simplified two-joint robotic arm where the two joints are connected by rigid links.Each joint has a mass, and the links are modeled as idealized rods. The motion of each jointaffects the other through the coupling of forces. The system can be modeled by the followingsecond-order coupled ODEs: m1θ1" + k1(θ1 − θrest) + k3(θ1 − θ2) = 0 (equation 1)m2θ2" + k2(θ2 − θrest) + k3(θ2 − θ1) = 0 (equation 2) where θ1(t) and θ2(t) represent the angular positions of the first and second joints, respec-tively. m1 and m2 are the effective masses at each joint. k1, k2 and k3 are the stiffnessconstants representing the elastic restoring forces in the joints and links. θrest = 0 representsthe equilibrium position for each joint.The parameters are:m1 = 1, m2 = 1, θrest = 0, k1 = 1, k2 = 2, k3 = 3, θrest = 0The initial conditions are:θ1(0) = 1, θ2(0) = 2Please solve by hand to get θ1(t) and θ2(t) using eigenvectors and eigenvalues. Show all steps/calculations, and provide a written description…arrow_forward3feet in 1secound; 21feet in x secondsarrow_forward(15 pts) Show your work to get full credit! Compute a QR factorization of the matrixarrow_forward
- (5) Let G be a group. Show that G acts on itself via the action g⚫a (i.e. using the binary operation of G) for all g, a Є G. [ for each of the three axioms, plus 1 for conclusion] = gaarrow_forward= (2) Let H {id, (12) (34), (13)(24), (14)(23)}. Prove that H is a sub- group of the symmetric group S4 of degree 4. each of the four axioms, plus 1 for the conclusion] 1 forarrow_forward(15 pts) Show your work to get full credit! Compute a singular value decomposition of the matrix A-( 7²)arrow_forward
- Sudoku Puzzle Rules Solving a Sudoku puzzle does not require the knowledge of mathematics but it does require logical thinking. A Sudoku puzzle is a grid of nine by nine squares or cells that have been subdivided into nine "regions" of three by three cells. Consider the following diagram: The objective of Sudoku is to enter a digit from 1 through 9 in each cell, in such a way that: Each horizontal row (shown in blue) contains each digit exactly once. Each vertical column (shown in pink) contains each digit exactly once. Each sub grid or region (shown in orange) contains each digit exactly once. In each Sudoku puzzle, some digits have already been entered, you may not change these. Your job is to fill the remaining cells with digits keeping in mind the three rules discussed above. Sudoku puzzles have become so popular that they can be found in newspapers and magazines around the world. If you are ever planning a long trip where you may be stuck in a car, Sudoku can help to pass the…arrow_forward(3) Let G be a group and let gЄ G. Prove that the function f : G→ G given by f(x) = gx is bijective (i.e. injective, and surjective). [ 2 for injectivity, 2 for surjectivity, 1 for bijectivity]arrow_forward(4) Let X = {(a,b) : a,bЄ Z, a on X given by (a, b) R(c, d) if ad 0,60}. Show that the relation R = bc is an equivalence relation. [ 1 for reflexivity, 1 for symmetry, 1 for transitivity, 1 for conclusion]arrow_forward
- (15 pts) Show your work to get full credit! Compute a diagonalization of the matrix -1 0 0 A = 0 1 1 0 20arrow_forward(1) Let G = R \ {1}. the set of all real numbers except 1. Show that G, together with the operation * given by x * y = x + y = xy for all x, y Є G, is a group. [5: 1 for each of the four axioms, and 1 for the conclusion] Hint: See Question 3.2 in the Course Notes for an example of how to write this down formally. See also Exercise 7 in Section 4.7 of [Groups, C. R. Jordan and D. A. Jordan], available online via the Libraryarrow_forwardInstructions: Instructions: Please show as much work as possible to clearly show the steps you used to find the solution. Part 1: In M4LE1 Hand-in Assignment you were to select a vehicle you would like to drive. In this hand-in assignment you are to choose a similar (or same) vehicle and find the cost to lease it. Describe the vehicle by stating make, model, special features, colour, et cetera. Find the price of the vehicle. You may look for the price at a dealer, in a newspaper, on TV, on the Internet, or source of your choice. Be sure to indicate the price and where you found the information. Assume that you have $5000 for a down payment to apply to the lease. Calculate the total cost of leasing the vehicle, including the down payment and applicable taxes. You may want to use a leasing calculator. Be sure to show how you arrived at your answer. Part 2: Compare the cost of buying the vehicle using your information from M4LE1 to the cost of leasing determined in Part 1. Would…arrow_forward
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill





