Chapter 1, Problem 1.5.6P

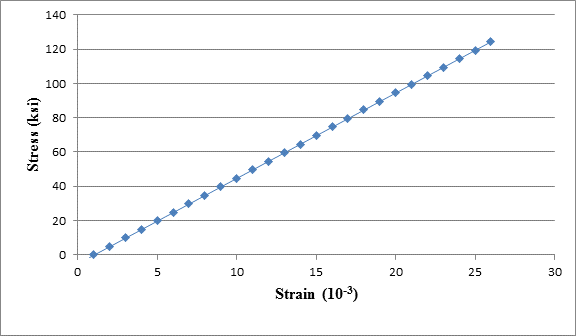
The data in Table 1.5.3 were obtained from a tensile test of a metal specimen with a rectangular cross section of $0.\text{2}0\text{11 in}{.}^{\text{2}}$ in area and a gage length (the length over which the elongation is measured) of 2.000 inches. The specimen was not loaded to failure.

a. Generate a table of stress and strain values.

b. Plot these values and draw a best-fit line to obtain a stress-strain curve.

c. Determine the modulus of elasticity from the slope of the linear portion of the curve.

d. Estimate the value of the proportional limit.

e. Use the $0.\text{2}\%$ offset method to determine the yield stress.