
Concept explainers
(a)
The value of the parameter b and plot the function by using half-life of carbon-14.
Answer to Problem 1.25P
The value of the parameter
Explanation of Solution
Given:
Half-life of carbon -14 is 5500 years
Concept Used:
Fraction of carbon -14 remaining time at
The exponential decay,
Calculation:
Obtain
Thus,
Substitute carbon half-life, 5500 years for
Thus the value of the parameter
Now the exponential decay function
Enter the following code in MATLAB:
The following is the plot of the exponential decay function:
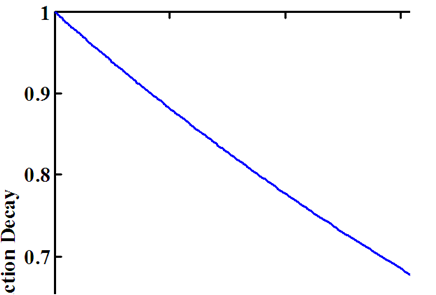
Figure 1.
Conclusion:
Thus, the value of the parameter
(b)
The time when the organism died.
Answer to Problem 1.25P
Organism died
Explanation of Solution
Given:
Half-life of carbon -14 is 5500 years.
Concept Used:
Fraction of carbon -14 remaining time at
The exponential decay,
Calculation:
We have,
Solve for t.
Conclusion:
Thus,organism died
(c)
The effect of b on the age obtained in part (b).
Answer to Problem 1.25P
The organism died age is reduced to
Explanation of Solution
Given:
Half-life of carbon-14 is 5500 years and
Concept Used:
Fraction of carbon - 14 remaining time at
The exponential decay,
Calculation:
Determine
Determine the time estimate
Conclusion:
Thus, the organism died age is reduced to
Want to see more full solutions like this?
Chapter 1 Solutions
System Dynamics
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





