You wish to test the following claim (HaHa) at a significance level of α=0.001α=0.001. Ho:p1=p2Ho:p1=p2 Ha:p1
Compound Probability
Compound probability can be defined as the probability of the two events which are independent. It can be defined as the multiplication of the probability of two events that are not dependent.
Tree diagram
Probability theory is a branch of mathematics that deals with the subject of probability. Although there are many different concepts of probability, probability theory expresses the definition mathematically through a series of axioms. Usually, these axioms express probability in terms of a probability space, which assigns a measure with values ranging from 0 to 1 to a set of outcomes known as the sample space. An event is a subset of these outcomes that is described.
Conditional Probability
By definition, the term probability is expressed as a part of mathematics where the chance of an event that may either occur or not is evaluated and expressed in numerical terms. The range of the value within which probability can be expressed is between 0 and 1. The higher the chance of an event occurring, the closer is its value to be 1. If the probability of an event is 1, it means that the event will happen under all considered circumstances. Similarly, if the probability is exactly 0, then no matter the situation, the event will never occur.
You wish to test the following claim (HaHa) at a significance level of α=0.001α=0.001.
Ho:p1=p2Ho:p1=p2
Ha:p1<p2Ha:p1<p2
You obtain 47 successes in a sample of size n1=208n1=208 from the first population. You obtain 182 successes in a sample of size n2=532n2=532 from the second population. For this test, you should NOT use the continuity correction, and you should use the
What is the test statistic for this sample? (Report answer accurate to three decimal places.)
test statistic =
What is the p-value for this sample? (Report answer accurate to four decimal places.)
p-value =
The p-value is...
- less than (or equal to) αα
- greater than αα
This test statistic leads to a decision to...
- reject the null
- accept the null
- fail to reject the null
As such, the final conclusion is that...
- There is sufficient evidence to warrant rejection of the claim that the first population proportion is less than the second population proportion.
- There is not sufficient evidence to warrant rejection of the claim that the first population proportion is less than the second population proportion.
- The sample data support the claim that the first population proportion is less than the second population proportion.
- There is not sufficient sample evidence to support the claim that the first population proportion is less than the second population proportion.
According to the provided data,
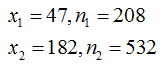
The null and alternative hypotheses are;
This is a lower-tailed test.
The level of significance, α = 0.001.
The sample proportions and pooled proportion is as:
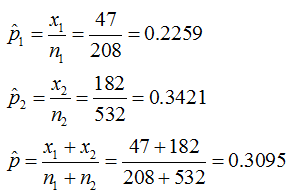
Step by step
Solved in 4 steps with 5 images
