Question
A cube of mass m is initially at rest at the highest point of an inclined plane, which has a height of 4.1 m and makes an angle of θ = 19° with respect to the horizontal. After letting go of the object, you notice it to be traveling at v = 0.65 m/s a distance d after the end of the inclined plane as shown. The coefficient of kinetic friction between the cube and the plane is μp = 0.1, and the coefficient of friction on the horizontal surface is μr = 0.2.
1)What is the speed of the cube, in meters per second, just after it leaves the inclined plane?
2) Find the distance, d, in meters.
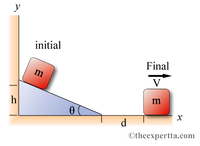
Transcribed Image Text:y
initial
Final
m
V
h
m
d
©theexpertta.com
Expert Solution
arrow_forward
Step 1
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Mary and her sister are playing with a cardboard box on the neighborhood hill. Mary climbs into the box, the total mass of the box with Mary in it is 115 kg. The box starts at rest at the beginning of the incline. The hill is at an incline of 28 degrees with respect to the horizontal.The static and kinectic friction between the box and hill is 0.4 and 0.2 respectively. Assume that Mary is now in the box, but has not started to move. a. What is the magnitude of the friction force acting on the box?b. What is the magnitude of the net force acting on the box and child system?c. Will the box slide down the hill, or stay at rest?arrow_forwardA brick of mass m is initially at rest at the peak of an inclined plane which has a height of 5.52m and has an angle of θ=20.3∘ with respect to the horizontal. After it has been released, it is found to be traveling at v=0.84m/s a distance d after the end of the inclined plane, as shown. The coefficient of kinetic friction between the brick and the plane is μp=0.1, and the coefficient of friction on the horizontal surface is μr=0.2. What is the speed of the brick, in meters per second, just after it leaves the inclined plane? Find the distance, d, in meters.arrow_forwardAs shown in the figure below, a box of mass m = 59.0 kg (initially at rest) is pushed a distance d = 80.0 m across a rough warehouse floor by an applied force of FA = 220 N directed at an angle of 30.0° below the horizontal. The coefficient of kinetic friction between the floor and the box is 0.100. Determine the following. (For parts (a) through (d), give your answer to the nearest multiple of 10.) (a) work done by the applied force WA = (b) work done by the force of gravity Wg = (c) work done by the normal force WN = (d) work done by the force of friction Wf = rough surface www (e) Calculate the net work on the box by finding the sum of all the works done by each individual force. W Net = J (f) Now find the net work by first finding the net force on the box, then finding the work done by this net force. W Net =arrow_forward
- A crate of mass m is initially at rest at the highest point of an inclined plane, which has a height of 4.7 m and has an angle of θ = 28° with respect to the horizontal. After it has been released, it is observed to be traveling at v = 0.85 m/s a distance d after the end of the inclined plane as shown. The coefficient of kinetic friction between the crate and the plane is μp = 0.1, and the coefficient of friction on the horizontal surface is μr = 0.2. Find the distance d, in meters.arrow_forwardThe car is fully loaded with passengers and has a total mass of 575 kg. At point A, the car is at the lowest point in a circular arc of radius r1 = 12.4 m. At point B, the car is at the highest point of a circular arc of radius r2 = 17.3 m. (a) If the car has a speed of 25.0 m/s at point A, what is the magnitude of the force (in N) of the track on the car at this point? (b) What is the maximum speed (in m/s) the car can have at point B in order for the car to maintain contact with the track at all times (that is, so that it does not "jump" off the track)?arrow_forwardThe system shown consists of 3 cables. For instance; cable C12 joins points 1 and 2. The coordinates of point 1 are (7.79, 0, 0) m, those of point 2 are (0, 7.58, 9.77) m, and those of point 3 are (0, 7.58, -9.77) m. The force P = 99 kN. Determine the force in cable C14.arrow_forward
- As shown in the figure below, a box of mass m = 30.0 kg is sliding along a horizontal frictionless surface at a speed v₁ = 4.55 m/s when it encounters a ramp inclined at an angle of 0 = 28.0⁰. frictionless surface The coefficient of kinetic friction between the ramp and the box is μ = 0.0704 and the box slides a distance d up the ramp before coming momentarily to rest. (a) Determine the distance (in m) the box slides up the ramp before coming momentarily to rest. Ο OW₁ = -APE Wg OW, m (b) Determine which of the following statements is most correct about the box traveling up the ramp and coming momentarily to rest. OW.. = AKE Net = W Net ΔΕ = W cons + W noncons ΔΕ = ΔΚΕ + ΔΡΕ Ο O all of these rough surface TTO nonconsarrow_forwardAs shown in the figure below, a box of mass m = 68.0 kg (initially at rest) is pushed a distanced = 69.0 m across a rough warehouse floor by an applied force of F = 236 N directed at an angle of 30.0° below the horizontal. The coefficient of kinetic friction between the floor and the box is 0.100. Determine the following. (For parts (a) through (d), give your answer to the nearest multiple of 10.) F 30 rough surface Iwwwwwwwwwwww (a) work done by the applied force WA = (b) work done by the force of gravity (c) work done by the normal force WN = (d) work done the force of friction W; = (e) Calculate the net work on the box by finding the sum of all the works done by each individual force. WNet = (f) Now find the net work by first finding the net force on the box, then finding the work done by this net force. WNet = Additional Materials O Readingarrow_forwardA block of mass m is initially at rest at the top of an inclined plane which has a height of 6.18m and makes an angle of θ=25.2∘ with respect to the horizontal. After being released, it is observed to be traveling at v=0.14m/s a distance d after the end of the inclined plane, as shown. The coefficient of kinetic friction between the block and the plane is μp=0.1, and the coefficient of friction on the horizontal surface is μr=0.2. Find the distance, d, in meters.arrow_forward
- In the figure, a rectangular slab of slate rests on a bedrock surface inclined at angle 8 = 22.8°. The slab has length L = 48.9 m, thickness T = 6.61 m, and width W = 12.7 m, and 1.0 cm³ of it has a mass of 3.2 g. The coefficient of static friction between slab and bedrock is 0.312. (a) Calculate the component of the gravitational force on the slab parallel to the bedrock surface. (b) Calculate the magnitude of the static frictional force on the slab. By comparing (a) and (b), you can see that the slab is in danger of sliding. This is prevented only by chance protrusions of bedrock. (c) To stabilize the slab, bolts are to be driven perpendicular to the bedrock surface (two bolts are shown). If each bolt has a cross-sectional area of 6.47 cm² and will snap under a shearing stress of 3.59 x 108 N/m², what is the minimum number of bolts needed? Assume that the bolts do not affect the normal force.arrow_forwardA crate of mass m is initially at rest at the highest point of an inclined plane which has a height of 5.28 m and makes an angle of A = 17.2° with respect to the horizontal. After it has been released, it is found to be traveling at v = 0.29 m/s a distance dafter the end of the inclined plane, as shown. The coefficient of kinetic friction between the crate and the plane is tp = 0.1, and the coefficient of friction on the horizontal surface is f4r = 0.2.arrow_forwardA basket of flowers of mass 3 kg is placed on a flat grassy slope that makes an angle θ with the horizontal. The coefficient of static friction between the basket and the slope is 0.45 and the basket is on the point of slipping down the slope. Model the basket of flowers as a particle and the grassy slope as a plane. Take the magnitude of the acceleration due to gravity, g, to be 9.8 m s−2 . State the forces that act on the basket. Draw a force diagram showing them, defining the symbols that you use to represent the forces and marking the sizes of the angles to show the directions of the forces. Take the unit vector i to point up the slope and the unit vector j to point upwards and perpendicular to the slope. Add these unit vectors to your force diagram.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios