
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
What is the radius and interval of convergence of this power series problem?
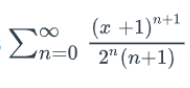
Transcribed Image Text:(x +1)"+1
Ln=02"(n+1)
100
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- 4. Determine if the series is absolutely convergent, conditionally convergent, or divergent using one of the following (divergence test, integral test, comparison test, limit comparison test, alternating series test, ratio test, root test).arrow_forward3. Without examining the convergence, find a power series generated by 1 f(x) = -at c = 5arrow_forward12. Determine if the series is absolutely convergent, conditionally convergent, or divergent using one of the following (divergence test, integral test, comparison test, limit comparison test, alternating series test, ratio test, root test).arrow_forward
- 27) Determine whether the following series converges: € (k-1)* k=4arrow_forwardCan you solve this using the flow given for determination of integrating factorarrow_forward12) There is one special “family” of series for which, if the series converges, we can determine the exact value of the series. This is the family where it really matters that we know the bounds of the summation. What family is this?arrow_forward
- This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the slipped part Tutorial Exercise Find the interval of convergence of the power series. (Be sure to include a check for convergence at the endpoints of the interval.) Step 1 (4x)" (an)! Recall the Ratio Test, which states that if a, is a series with nonzero terms, and lim 1, or lim 1 For any fixed value of x such that x 0, let a (4x)" (an)! and find lim 518 (4x)+1 lim 518 = lim (3(n+1)) 719 (a) (3n) (3n)! (4x)+1) = - (3(n+1))! 880.0 (-00,00) X Step 2 By the Ratio Test, the series converges if lim Submit Skip (you cannot come back) 518 1. Therefore, the series converges for x such that lim =, then, divergesarrow_forwardIn the problem, find the circle and radius of convergence of the given power series:arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

