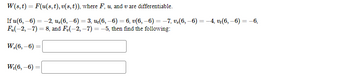
W(s, t) = F(u(s, t), v(s, t)), where F. u. and v are differentiable. If u (6,-6)= -2, u,(6, −6) = 3, ut(6, −6) = 6, v(6, −6) = −7. v,(6, −6) = −4, vr(6, −6) = −6, Fu(-2,-7)=8, and F(-2,-7)=-5, then find the following: W,(6,-6) W₂(6, -6)

Consider a function z = F(u(s, t), v(s, t)) where F, u, and u are differentiable and u(8, 6) = -1, v(8, 6) = 2, u, (8, 6) = 5, u, (8, 6) = 9, vs(8, 6) = −3, v₁(8, 6) = 4, Fu(-1,2) = -4, and F(-1,2)= -10. Compute and when s = 8 and t = 6 dt

Find f (x,y) and f(x,y). Then find fx (2,-1) and fy(-4,3). f(x,y)= In 5x¹ +8x²y²| fx(x,y)= E f(x,y) = el nd-a Эх dent 1,(2,-1)- fy(-4,3)= ulus unct (x.y)= =es › le he Ge x0) + fy ne point E a SL

Let W(s, t) = F(u(s, t), v(s, t)), where F, u, and v are differentiable, and the following applies. v(3,-2) = 0 Vs(3,-2) = 5 u(3,-2) = -3 Us(3,-2) = -7 ut(3,-2) = 7 Fu(-3,0) = -9 Vt(3,-2) = -1 Fv(-3,0) = -5 Find Wę(3,-2) and We(3,-2). Ws(3,-2) = W+(3,-2) =

Let f(x, y) = xy² and r(t) = (¹/1²,t³). Calculate Vf. (Use symbolic notation and fractions where needed. Express numbers in exact form. Give your answer in the form (*, *). ) Vf= Calculate r' (t). (Use symbolic notation and fractions where needed. Express numbers in exact form. Give your answer in the form (*, *). ) r' (t) = Use the Chain Rule for Paths to evaluateƒ(r(t)) at t = 1.5. (Use decimal notation. Give your answer to three decimal places.) d dt - ƒ(r(1.5)) = = Use the Chain Rule for Paths to evaluate ƒ(r(t)) at t = -1.7. (Use decimal notation. Give your answer to three decimal places.) d dt d f(r(-1.7)) =