
Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
18th Edition
ISBN: 9780079039897
Author: Carter
Publisher: McGraw Hill
expand_more
expand_more
format_list_bulleted
Question
please solve this problem step by step and make it quick please
Transcribed Image Text:While her husband spent 2½ hours picking out new speakers, a statistician decided to determine whether the percent of men who enjoy shopping for electronic equipment is higher than the percent of women who enjoy
shopping for electronic equipment. The population was Saturday afternoon shoppers. Out of 65 men, 25 said they enjoyed the activity. Eight of the 25 women surveyed claimed to enjoy the activity. Interpret the results of the
survey. Conduct a hypothesis test at the 5% level. Let the subscript m = men and w = women.
NOTE: If you are using a Student's t-distribution for the problem, including for paired data, you may assume that the underlying population is normally distributed. (In general, you must first prove that assumption, though.)
Part (a)
State the null hypothesis.
○ Ho: Pm > Pw
Ho: Pm² Pw
Ho: Pm Pw
Ho: Pm Pw
Part (b)
State the alternative hypothesis.
OH Pm Pw
Ha- Pm * Pw
O Ha: Pm Pw
OH₂- Pm = Pw
Part (c)
In words, state what your random variable P'm-P'w represents.
OP'm-P'w represents the proportion of people who enjoy shopping for electronics.
OP'm-P'w represents the difference in the proportion of men who enjoy shopping for electronics and women who enjoy shopping for electronics.
OP'm-P'w represents the difference in the average number of men who enjoy shopping for electronics and women who enjoy shopping for electronics.
OP'm-P'w represents the difference between the number of men who enjoy shopping for electronics and women who enjoy shopping for electronics.
Part (d)
State the distribution to use for the test. (Round your answers to four decimal places.)
P'm-P'w~
Part (e)
What is the test statistic? (If using the z distribution round your answer to two decimal places, and if using the t distribution round your answer to three decimal places.)
-Select---
Part (f)
What is the p-value? (Round your answer to four decimal places.)
Explain what the p-value means for this problem.
○ If Ho is true, then there is a chance equal to the p-value that the proportion of men who enjoy shopping for electronic equipment is 0.0646 lower than the proportion of women who enjoy shopping for electronic equipment.
○ If Ho is false, then there is a chance equal to the p-value that the proportion of men who enjoy shopping for electronic equipment is at least 0.0646 higher than the proportion of women who enjoy shopping for electronic equipment.
If Ho is true, then there is a chance equal to the p-value that the proportion of men who enjoy shopping for electronic equipment is at least 0.0646 higher than the proportion of women who enjoy shopping for electronic equipment.
If Ho is false, then there is a chance equal to the p-value that the proportion of men who enjoy shopping for electronic equipment is 0.0646 lower than the proportion of women who enjoy shopping for electronic equipment.
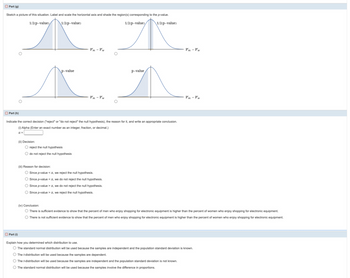
Transcribed Image Text:Part (g)
Sketch a picture of this situation. Label and scale the horizontal axis and shade the region(s) corresponding to the p-value.
1/2(p-value)
1/2(p-value)
1/2(p-value)
1/2(p-value)
ལ་ལས་ང་ལས་ ་ ་ ་ ་ ་ས་མ་ཀ་ར་ས་ ་ ་
p-value
p-value
K....
P'm-Pw
P'm - Pw
Part (h)
Indicate the correct decision ("reject" or "do not reject" the null hypothesis), the reason for it, and write an appropriate conclusion.
(i) Alpha (Enter an exact number as an integer, fraction, or decimal.)
α=>
(ii) Decision:
◇ reject the null hypothesis
○ do not reject the null hypothesis
(iii) Reason for decision:
O Since p-value <a, we reject the null hypothesis.
Since p-value <a, we do not reject the null hypothesis.
○ Since p-value>a, we do not reject the null hypothesis.
○ Since p-value>a, we reject the null hypothesis.
(iv) Conclusion:
◇ There is sufficient evidence to show that the percent of men who enjoy shopping for electronic equipment is higher than the percent of women who enjoy shopping for electronic equipment.
There is not sufficient evidence to show that the percent of men who enjoy shopping for electronic equipment is higher than the percent of women who enjoy shopping for electronic equipment.
Part (i)
Explain how you determined which distribution to use.
The standard normal distribution will be used because the samples are independent and the population standard deviation is known.
The t-distribution will be used because the samples are dependent.
The t-distribution will be used because the samples are independent and the population standard deviation is not known.
The standard normal distribution will be used because the samples involve the difference in proportions.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Recommended textbooks for you
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL

Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill

Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL