
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Question
The CSV file modeldata.csv contains 200 observations of 4 explanatory variables (x1, x2, x3, x4) and a response variable (y). A multiple linear regression model is built in R using the following code,
> modeldata <- read.csv("modeldata.csv") > x1 <- modeldata$x1 > x2 <- modeldata$x2 > x3 <- modeldata$x3 > x4 <- modeldata$x4 > y <- modeldata$y > model <- lm(y~x1+x2+x3+x4)Question: What this particular plot shows about the model being analysed?
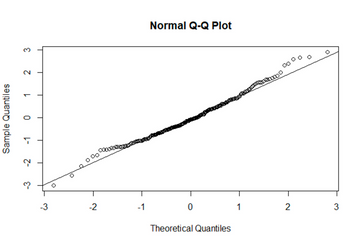
Transcribed Image Text:Sample Quantiles
-3
-2 -1
0 1
-3
2
3
0.00
0000
-2
-1
0
Theoretical Quantiles
Normal Q-Q Plot
00
1
2
3
00
0
0
о
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps

Knowledge Booster
Similar questions
- We expect a car's highway gas mileage to be related to its city gas mileage (in miles per gallon, mpg). Data for all 1259 vehicles in the government's 2019 Fuel Economy Guide give the regression line highway mpg = 8.720+ (0.914x city mpg) for predicting highway mileage from city mileage. O Macmillan Learning (c) Find the predicted highway mileage, y, for a car that gets 14 mpg in the city. Give your answer to three decimal places. y = mpg Find the predicted highway mileage, y, for a car that gets 21 mpg in the city. Give your answer to three decimal places. y = mpgarrow_forwardThe following table shows the starting salary and profile of a sample of 10 employees in a certain call center agency. Run a multiple regression analysis with starting salary as the dependent variable (pesos) and GPA, years of experience and civil service ratings as the independent variables. Use .05 level of significance.What is the equation of the resulting multiple linear regression? starting_salary = 3008.61 + 48.65*GPA + 94.79*years_of_experience + 27.36*civil_service_ratings starting_salary = 15000.00 + 48.65*GPA + 94.79*years_of_experience + 27.36*civil_service_ratings starting_salary = 15001.00 + 41.43*GPA + 84.71*years_of_experience + 37.32*civil_service_ratings starting_salary = 2366.77 + 130.25*GPA + 396.39*years_of_experience + 21.67*civil_service_ratingsarrow_forwardPlease answer as many as your allowed too. Thank you :) A regression was run to determine if there is a relationship between the happiness index (y) and life expectancy in years of a given country (x).The results of the regression were: ˆyy^=a+bxa=-1.68b=0.168 (a) Write the equation of the Least Squares Regression line of the formˆyy^= + x(b) Which is a possible value for the correlation coefficient, rr? -1.417 1.417 0.702 -0.702 (c) If a country increases its life expectancy, the happiness index will increase decrease (d) If the life expectancy is increased by 0.5 years in a certain country, how much will the happiness index change? Round to two decimal places.(e) Use the regression line to predict the happiness index of a country with a life expectancy of 69 years. Round to two decimal places.arrow_forward
- The CSV file modeldata.csv contains 200 observations of 4 explanatory variables (x1, x2, x3, x4) and a response variable (y). A multiple linear regression model is built in R using the following code, > modeldata <- read.csv("modeldata.csv") > x1 <- modeldata$x1 > x2 <- modeldata$x2 > x3 <- modeldata$x3 > x4 <- modeldata$x4 > y <- modeldata$y > model <- lm(y~x1+x2+x3+x4) Question: What this particular plot shows about the model being analysed?arrow_forwardA company that manufactures computer chips wants to use a multiple regression model to study the effect that 3 different variables have on y, the total daily production cost (in thousands of dollars). Let B,, B,, and B, denote the coefficients of the 3 variables in this model. Using 22 observations on each of the variables, the software program used to find the estimated regression model reports that the total sum of squares (SST) is 485.84 and the regression sum of squares (SSR) is 229.91. Using a significance level of 0.10, can you conclude that at least one of the independent variables in the model provides useful (i.e., statistically significant) information for predicting daily production costs? Perform a one-tailed test. Then complete the parts below. Carry your intermediate computations to three or more decimal places. (a) State the null hypothesis H, for the test. Note that the alternative hypothesis H, is given. H, :0 H, : at least one of the independent variables is useful…arrow_forwardAn airline developed a regression model to predict revenue from flights that connect "feeder" cities to its hub airport. The response in the model is the revenue generated by flights operating to the feeder cities (in thousands of dollars per month), and the two explanatory variables are the air distance between the hub and feeder city (Distance, in miles) and the population of the feeder city (in thousands). The least squares regression equation based on data for 37 feeder locations last month is Estimated revenue = 81 +0.3Distance + 1.4Population with R² = 0.75 and so = 31.2. Complete parts a through d. (a) The airline plans to expand its operations to add an additional feeder city. The first possible city has population 150,000 and is 275 miles from the hub. A second possible city has population 180,000 and is 250 miles from the hub. Which would you recommend if the airline wants to increase total revenue? The first city The second cityarrow_forward
- The table below gives the number of hours spent unsupervised each day as well as the overall grade averages for seven randomly selected middle school students. Using this data, consider the equation of the regression line, yˆ=b0+b1xy^=b0+b1x, for predicting the overall grade average for a middle school student based on the number of hours spent unsupervised each day. Keep in mind, the correlation coefficient may or may not be statistically significant for the data given. Remember, in practice, it would not be appropriate to use the regression line to make a prediction if the correlation coefficient is not statistically significant. Hours Unsupervised 00 0.50.5 11 1.51.5 22 3.53.5 44 Overall Grades 8989 8181 7373 7272 6969 6767 6363 Table Copy Data Step 6 of 6: Find the value of the coefficient of determination. Round your answer to three decimal places.arrow_forwardIn a study of 1991 model cars, a researcher computed the least-squares regression line of price (in dollars) on horsepower. He obtained the following equation for this line. Price = – 6677 + 175× Horsepower Based on the least-squares regression line, what would we predict the cost to be of a 1991 model car with horsepower equal to 200? If the actual cost of a 1991 car with 200 horsepower is $27500, what is the residual? Is the predictionan underestimate or an overestimate? What does the slope of 175 and y intercept of (0,-6677) mean in the context of the problem? The coefficient of determination is ?2=84%. Interpret in the context of the problem. Find the correlation and interpret.arrow_forwardThe table below gives the number of hours spent unsupervised each day as well as the overall grade averages for seven randomly selected middle school students. Using this data, consider the equation of the regression line, yˆ=b0+b1xy^=b0+b1x, for predicting the overall grade average for a middle school student based on the number of hours spent unsupervised each day. Keep in mind, the correlation coefficient may or may not be statistically significant for the data given. Remember, in practice, it would not be appropriate to use the regression line to make a prediction if the correlation coefficient is not statistically significant. Hours Unsupervised 1.51.5 2.52.5 33 44 4.54.5 55 66 Overall Grades 9494 9292 8282 7979 7171 7070 6262 Find the value of the coefficient of determination. Round your answer to three decimal places.arrow_forward
- The CSV file modeldata.csv contains 200 observations of 4 explanatory variables (x1, x2, x3, x4) and a response variable (y). A multiple linear regression model is built in R using the following code, > modeldata <- read.csv("modeldata.csv") > x1 <- modeldata$x1 > x2 <- modeldata$x2 > x3 <- modeldata$x3 > x4 <- modeldata$x4 > y <- modeldata$y > model <- lm(y~x1+x2+x3+x4) Question: What this particular plot shows about the model being analysed?arrow_forwardAn engineer is testing a new car model to determine how its fuel efficiency, measured in L/(100 km), is related to its speed, which is measured in km/hour. The engineer calculates the average speed for 30 trials. The average speed is an example of a (statistic or parameter) The engineer would like to find the least squares regression line predicting fuel used (y) from speed (x) for the 30 cars he observed. He collected the data below. Speed 62 65 80 82 85 87 90 96 98 100 Fuel 12 13 14 13 14 14 15 15 16 15 Speed 100 102 104 107 112 114 114 117 121 122 Fuel 16 17 16 17 18 17 18 17 18 19 Speed 124 127 127 130 132 137 138 142 144 150 Fuel 18 19 20 19 21 23 22 23 24 26 The regression line equation is Round each number to four decimal places.arrow_forwardA year-long fitness center study sought to determine if there is a relationship between the amount of muscle mass gained y(kilograms) and the weekly time spent working out under the guidance of a trainer x(minutes). The resulting least-squares regression line for the study is y=2.04 + 0.12x A) predictions using this equation will be fairly good since about 95% of the variation in muscle mass can be explained by the linear relationship with time spent working out. B)Predictions using this equation will be faily good since about 90.25% of the variation in muscle mass can be explained by the linear relationship with time spent working out C)Predictions using this equation will be fairly poor since only about 95% of the variation in muscle mass can be explained by the linear relationship with time spent working out D) Predictions using this equation will be fairly poor since only about 90.25% of the variation in muscle mass can be explained by the linear relationship with time spent…arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman