
Computer Networking: A Top-Down Approach (7th Edition)
7th Edition
ISBN: 9780133594140
Author: James Kurose, Keith Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question

Transcribed Image Text:We will write our own (Python) function to calculate the (mathematical) sine function. One obvious way is to evaluate the Taylor series:
ř-1)=-1,2n–1
(2n – 1)!
73
sin x = x -
+
3!
5!
7!
n=1
A small trick will come in useful here. As n gets larger (and we will certainly need to add lots of terms to get an accurate result!) it will take longer and longer to calculate both x2n and (2n – 1)!.
However, both of these are easy to calculate given the previous term. So the smart way to evaluate this series is to keep track of the previous term added, and then use a recursive relationship
tn = tn-1 x
(2n – 1)(2n – 2)
Check that you understand how this works, then write a function sine_sum(x) to calculate sin(x) by this method.
Expert Solution
arrow_forward
Step 1
we need to find sine_sum(x) function using recursion formula:
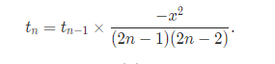
Step by stepSolved in 3 steps with 4 images

Knowledge Booster
Similar questions
- Plot (as a function of angular frequency), the magnitude and the phase of the impedance resulting from a resistor (1.2 kOhm) and inductor (1.5 mH) in parallel. Use a logarithmic axis for the frequency, and for the magnitude. Use the range [10, 10**10] rad/s. The impedance of an inductance L is ???Ljω. Label axes. In python and can use cmath if neededarrow_forwardHow do I do (K+1)? Please use step by step simply pleasearrow_forwardWrite equivalent expressions for each of the following by using De Morgan’s Law. A. !(x < 5) B. !(y > 2 && !found ) C. !(c == ‘r’ || (( y > 2) && !found ))arrow_forward
- Please do the following question with the required python coding. Question is in the photo.arrow_forwardSuppose that you want to calculate 1434661 · 3785648743 − 100020304 · 54300201. You are told thatthe answer is a positive integer less than 90. Compute the answer mod 10 and mod 9, then combineto get the answer. Show all the necessary work to obtain your answers. Note: This technique hasoften been employed to do calculations with large integers because most of the computations use smallintegers, with only the Chinese Remainder Theorem step requiring large integers. For example, if theanswer is known to be less than 1036, the calculations can be done mod p for each prime less than100. Since the product of the primes less than 100 is approximately 2.3 × 1036, the Chinese RemainderTheorem gives the answer exactlyarrow_forwardConsider the formula rv p→qv¬r Fill in the blanks with names of the columns of a truth table for this formula. To insert special symbols, copy them from the given formula. If there is more than one way to label columns, put them in left to right order. Do not simplify the formula. For example, if the formula is (p →q) ^ - p, then insert the following in the five blanks (without numbers, numbers are just to denote which blank it is): 1) p 2) q 3) p q 4) -p 5) (p →q) ^ ¬p Note that the variable columns are labeled in alphabetical order (p, then q, then r...), p →q is listed before -p (left to right), and there are no outer parentheses on any formulas.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON
Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science
Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning
Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning
Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education
Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY
Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY

Computer Networking: A Top-Down Approach (7th Edi...
Computer Engineering
ISBN:9780133594140
Author:James Kurose, Keith Ross
Publisher:PEARSON

Computer Organization and Design MIPS Edition, Fi...
Computer Engineering
ISBN:9780124077263
Author:David A. Patterson, John L. Hennessy
Publisher:Elsevier Science

Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:9781337569330
Author:Jill West, Tamara Dean, Jean Andrews
Publisher:Cengage Learning

Concepts of Database Management
Computer Engineering
ISBN:9781337093422
Author:Joy L. Starks, Philip J. Pratt, Mary Z. Last
Publisher:Cengage Learning

Prelude to Programming
Computer Engineering
ISBN:9780133750423
Author:VENIT, Stewart
Publisher:Pearson Education

Sc Business Data Communications and Networking, T...
Computer Engineering
ISBN:9781119368830
Author:FITZGERALD
Publisher:WILEY