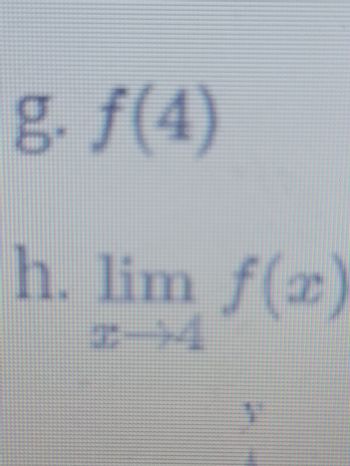
Hi! This question has 8 subparts. I need the last two G through H. Thank you! Here is the transcription of the image content, formatted for an educational website:---## Mathematical Problemsg. \( f(4) \)h. \( \lim_{{x \to 4}} f(x) \)---### Explanation:The problems presented involve two fundamental concepts in calculus and function analysis:1. **Function Evaluation (g)**: - The expression \( f(4) \) represents the value of the function \( f \) when the input \( x \) is 4. To solve this, one would substitute the value 4 into the function \( f \) and calculate the result.2. **Limit of a Function (h)**: - \( \lim_{{x \to 4}} f(x) \): This notation represents the limit of the function \( f(x) \) as \( x \) approaches 4. It involves analyzing the behavior of the function \( f \) in the vicinity of \( x = 4 \), but not necessarily at \( x = 4 \).---Understanding these concepts is crucial for mastering higher-level mathematics, including calculus and analysis. Further explanations and examples can be found in the resources provided on this site. **Graph Analysis:**In this diagram, we observe the graphical representation of a mathematical function, featuring key points and characteristics. The x-axis and y-axis both span from -6 to 6, encompassing a portion of the Cartesian plane. The graph comprises various curves and distinct markers representing critical points.### Key Features of the Graph:1. **Axes:** - The x-axis is labeled from -6 to 6. - The y-axis is also labeled from -6 to 6.2. **Curves:** - The graph displays a function that appears to be broken into multiple segments, each of which exhibits unique behaviors.3. 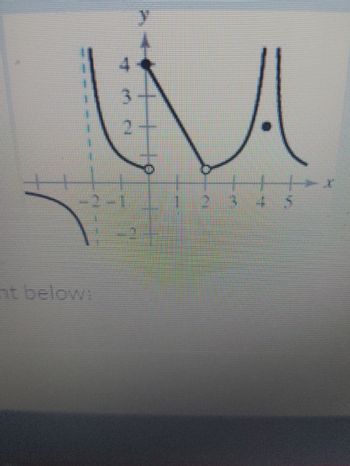**Points:** - There are several significant points marked on the graph: - The point (1, 4) is solid, indicating it is included in the function. - There are points at (2, 3) and (3, 3) marked with circles, representing points excluded from the function. - The point (3, 1) is solid, indicating it is included in the function. - An additional point is located at (4, 4). This point is solid, indicating inclusion in the function.### Detailed Function Behavior:- As x approaches 2, there is an open circle indicating a discontinuity at y = 3.- Moving along the x-axis, there is another open circle at (3, 3), followed by a solid point at (3, 1), suggesting a function shift or jump.- Another segment proceeds from x = 3 onwards, with a solid increasing curve towards x = 4, where y reaches 4, represented by another solid point.This graph could represent a piecewise function with specific inclusions and exclusions at marked points, highlighting important discontinuities. This is useful in understanding advanced mathematical concepts such as limits, continuity, and piecewise functions.

Answered: Image /qna-images/answer/353e623a-c2b5-4bf8-9a8b-c4d5dc6cdd2d.jpg

Answered: WA # | bartleby

WA #

8th Edition

ISBN:9781285741550

Author:James Stewart

Publisher:James Stewart

Chapter1: Functions And Models

Section: Chapter Questions

Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...

Similar questions

Hello, please answer all parts if possible. if not, please answer c, e and f, thank you.
what are the values of s1 and s2?
Detif Diverger.ce Colve CoNergence or 2. (-1 n²
please answer the questions i sent, exactly in the form of the question thank you so much
Help
Break down for me to understand
i need the answer quickly
The value of y is between negative three and positive eight inclusive. Which of the following represents y?