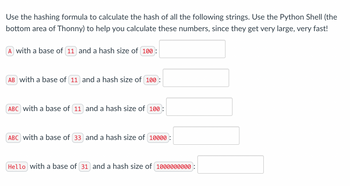
Use the hashing formula to calculate the hash of all the following strings. Use the Python Shell (the bottom area of Thonny) to help you calculate these numbers, since they get very large, very fast! A with a base of 11 and a hash size of 100: AB with a base of 11 and a hash size of 100: ABC with a base of 11 and a hash size of 100: ABC with a base of 33 and a hash size of 10000: Hello with a base of 31 and a hash size of 1000000000:

i need help with this

Don't copy from other website Unique answer plzz

text file 80 1 2 3 100 100 100 1001 0 2 100 3 4 100 1002 2 0 4 4 100 5 1003 100 4 0 100 100 4 100100 3 4 100 0 3 3 3100 4 100 100 3 0 100 1100 100 5 4 3 100 0 2100 100 100 100 3 1 2 0 My code below. I am getting an error when trying to create my adjacency matrix. i dont know what i am doing wrong def readMatrix(inputfilename):    ''' Returns a two-dimentional array created from the data in the given file.            Pre:  'inputfilename' is the name of a text file whose first row contains the            number of vertices in a graph and whose subsequent rows contain the rows of            the adjacency matrix of the graph. '''        # Open the file    f = open(inputfilename, 'r')     # Read the number of vertices from the first line of the file    n = int(f.readline().strip())     # Read the rest of the file stripping off the newline characters and splitting it into    # a list of intger values    rest = f.read().strip().split()         # Create the adjacency matrix    adjMat = []…

JAVA: Use the "natural split" algorithm on the file split.txt and answer the following question: How many elements are in the first list?   Split.txt file 200494 774 644 345 521 61 27 28 584 569 66 857 210 2 211 675 548 596 188 647 671 517 408 475 615 113 731 522 850 17 640 940 556 517 602 935 76 578 880 428 168 394 381 497 247 368 137 138 619 973 895 106 838 45 921 800 681 660 490 427 937 917 786 959 152 604 837 749 684 963 926 963 988 492 385 458 788 7 62 46 932 996 787 634 34 616 71 128 686 578 923 532 933 545 100 224 895 595 342 933 934 797 120 565 495 884 237 648 843 599 157 843 192 279 301 649 382 881 667 178 126 746 44 601 22 52 769 708 991 83 447 786 525 168 328 922 153 367 22 689 834 774 93 110 547 597 644 726 237 20 370 573 391 225 750 897 956 839 951 455 8 509 746 338 576 276 277 341 274 891 723 53 966 271 50 990 493 823 833 306 619 461 768 832 736 759 920 451 549 833 911 123 907 225 252 179 177 272 747 859

This is the code: String name = Doe, John"; int index =name.indexOf(" , "); String firstName= name.substring(index + 2, name.length()); System.out.println(firstName);

Java Programming: Write a lexer that prints out the shank.txt. Below is the shank.txt that needs to be printed out as a series of tokens and attached is the rubric of all the components the lexer needs to have.  Shank.txt Fibonoacci (Iterative) define add (num1,num2:integer var sum : integer)variable counter : integerFinonacci(N)int N = 10;while counter < Ndefine start ()variables num1,num2,num3 : integeradd num1,num2,var num3{num1 and num2 are added together to get num3}num1 = num2;num2 = num3;counter = counter + 1; GCD (Recursive) define add (int a,int b : gcd)if b = 0sum = asum gcd(b, a % b) GCD (Iterative) define add (inta, intb : gcd)if a = 0sum = bif b = 0sum = awhile counter a != bif a > ba = a - b;elseb = b - a;sum = a;variables a,b : integera = 60b = 96subtract a,b

I ran the code and there are lots of errors in the code. Attached are images of the errors. Make sure to fix those errors and there must be no error in the code at all.

I need help finding out what to put in the: encryptedArray[index] = encrypt(messageArray);//pass something to encrypt from the array System.out.print(messageArray);//print encrypted version portion of the coding as well as how to call the "encryptAll" method

Java Programming   This week's project involves a text file with that holds all of the novel Don Quixote*, by Miguel Cervantes. The text file has been heavily processed. It contains only lowercase letters, spaces, and new lines. That is a good format for counting words. Write code that reads through the text file one word at a time using a Scanner, and the next() method. Put the words into a HashMap, where the words are used as keys, and the values are Integers used to keep track of how many times the words occur in the text. If the text was "one fish two fish red fish blue fish one two three" then the HashMap would look like this:         key                value         "one"....        2         "fish"...        4         "two"....        2         "red"....        1         "blue"...        1         "three"..        1   Once you have created such a HashMap for the whole of the text you can write logic that prints out the answers to these questions: How many times does each of…