Computer Networking: A Top-Down Approach (7th Edition)
7th Edition
ISBN: 9780133594140
Author: James Kurose, Keith Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Related questions
Question
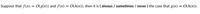
Transcribed Image Text:Suppose that \( f(n) = O(g(n)) \) and \( f(n) = O(h(n)) \), then it is ( **always** / sometimes / never ) the case that \( g(n) = O(h(n)) \).
Expert Solution
arrow_forward
Step 1
Defined the given statement always, sometimes or never
Step by stepSolved in 2 steps
Knowledge Booster
Similar questions
- Big-O notation is defined as follows: The function f(n) is O(g(n)) if there are positive integers c and N such that f(n) ≤ c · g(n) for all n > N. Is the relation “f(n) is O(g(n))” reflexive? symmetric? transitive? Justify your answers. “Θ(g(n))” is defined as follows: f(n) is Θ(g(n)) if and only if (f(n) is O(g(n)) & g(n) is O(f(n))). Is the relation “f(n) is Θ(g(n))” reflexive? symmetric? transitive? Justify your answersarrow_forwardYou are given a N*N maze with a rat placed at maze[0][0]. Find whether any path exist that rat can follow to reach its destination i.e. maze[N-1][N-1]. Rat can move in any direction ( left, right, up and down).Value of every cell in the maze can either be 0 or 1. Cells with value 0 are blocked means rat cannot enter into those cells and those with value 1 are open.Input FormatLine 1: Integer NNext N Lines: Each line will contain ith row elements (separated by space)Output Format :The output line contains true if any path exists for the rat to reach its destination otherwise print false.Sample Input 1 :31 0 11 0 11 1 1Sample Output 1 :trueSample Input 2 :31 0 11 0 10 1 1Sample Output 2 : false Solution: //// public class Solution { public static boolean ratInAMaze(int maze[][]){ int n = maze.length; int path[][] = new int[n][n]; return solveMaze(maze, 0, 0, path); } public static boolean solveMaze(int[][] maze, int i, int j, int[][] path) {//…arrow_forwardMaster theorem: if n< d T(n) = |aT(n/b)+ f (n) if n2 d 1. if f(n) is O(n - ), then T(n) is O(nos") 2. if f(n) is O(n' 3. if f(n) is 2(n® provided af (n/b)S (n) for some 8arrow_forwardplease explain how to do this and explain the answer.arrow_forwardFor each of the following pairs of functions fln)f(n) and g(n)g(n), determine whether Ofin))=0(g(n)). Don't just indicate “yes" or "no"; provide your reasoning. a. f(n) = log n² g(n) = log n + 5. b. f(n) = Vn g(n) = log n². c. f(n) = log² n g(n) = log n. d. f(n) = n g(n) = log² n.arrow_forwardes remaining 8. Consider the function f:NxN-N defined recursively by: 1) Base case: Let meN and define (0,m) = 0 2) Recursive case: For any x,meN, x>0, define f(x,m) = (x-1,m) + (m+m) Prove the following theorem holds using proof by induction: Thereom: For any n,meN, m>0 we have (n.m) I m = n+n Fill in your answer here 9 Help BIU X, x L - ɔE =N E X Formatarrow_forwardExplain, with an example why the following definition, would not be suitable or useful: f(n) is Ω( g(n) ) if and only if there exists n0, such that:forall n ≥ n0, there exists c > 0 such that,f(n) ≥ c g(n)arrow_forwardQ7. The big O bound for the following functions is T(n)= nlogn2+ nlogn OO (log(log n)) OO (nlogn) 00 (n² log n) 00 (n²)arrow_forward7. Prove or disprove: f(n) + g(n) = 0 (min(f(n), g(n)))arrow_forwardYou are given a N*N maze with a rat placed at maze[0][0]. Find whether any path exist that rat can follow to reach its destination i.e. maze[N-1][N-1]. Rat can move in any direction ( left, right, up and down).Value of every cell in the maze can either be 0 or 1. Cells with value 0 are blocked means rat cannot enter into those cells and those with value 1 are open.Input FormatLine 1: Integer NNext N Lines: Each line will contain ith row elements (separated by space)Output Format :The output line contains true if any path exists for the rat to reach its destination otherwise print false.Sample Input 1 :31 0 11 0 11 1 1Sample Output 1 :trueSample Input 2 :31 0 11 0 10 1 1Sample Output 2 : false Solution: //// public class Solution { public static boolean ratInAMaze(int maze[][]){ int n = maze.length; int path[][] = new int[n][n]; return solveMaze(maze, 0, 0, path); } public static boolean solveMaze(int[][] maze, int i, int j, int[][] path) {//…arrow_forward7. For n 2 1, in how many out of the n! permutations T = (T(1), 7(2),..., 7 (n)) of the numbers {1, 2, ..., n} the value of 7(i) is either i – 1, or i, or i +1 for all 1 < i < n? Example: The permutation (21354) follows the rules while the permutation (21534) does not because 7(3) = 5. Hint: Find the answer for small n by checking all the permutations and then find the recursive formula depending on the possible values for 1(n).arrow_forward2) Prove divisible by 3 for any integer nzo. that n(n²+s) is divisible by 3 for Let n 1 1 (1² +5) = 1(1+5)=(6/ K(K²+5) K+ 1 ((k + 1 ) ² + 5arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
- Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON
Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science
Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning 
Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning
Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education
Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY
Computer Networking: A Top-Down Approach (7th Edi...
Computer Engineering
ISBN:9780133594140
Author:James Kurose, Keith Ross
Publisher:PEARSON
Computer Organization and Design MIPS Edition, Fi...
Computer Engineering
ISBN:9780124077263
Author:David A. Patterson, John L. Hennessy
Publisher:Elsevier Science
Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:9781337569330
Author:Jill West, Tamara Dean, Jean Andrews
Publisher:Cengage Learning
Concepts of Database Management
Computer Engineering
ISBN:9781337093422
Author:Joy L. Starks, Philip J. Pratt, Mary Z. Last
Publisher:Cengage Learning
Prelude to Programming
Computer Engineering
ISBN:9780133750423
Author:VENIT, Stewart
Publisher:Pearson Education
Sc Business Data Communications and Networking, T...
Computer Engineering
ISBN:9781119368830
Author:FITZGERALD
Publisher:WILEY