
Concept explainers
The senior vice president for marketing at Kean Hotel believes that the company’s recentadvertising of the hotel has decreased the average room idle rate. To test the hypothesis, random sample of daily idle rates (in percentages) before the advertising is collected. A similar random sample of daily idle rates is collected after the advertising took place. The data are as follows.
Is there evidence that the average room idle rate of the hotel has decreased after the advertising at the 0.01 level of significance.
(Show me every step including pre-step and post-step for full credit)
|
Before (%) |
8 |
17 |
12 |
21 |
19 |
10 |
|
After (%) |
6 |
3 |
1 |
11 |
7 |
8 |
Given data and calculation for mean and standard deviation is shown below-
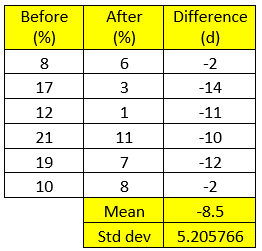
Calculate mean using excel function-
=AVERAGE(-2:-2)
And standard deviation-
=STDEV.S(-2:-2)
Step by stepSolved in 2 steps with 2 images

- A national online business magazine reports that the average cost of a speeding ticket in Miami, including court fees, is $220. A local police department claims that this amount has increased. To test their claim, they collect data from a simple random sample of 16 drivers who have been fined for speeding in the last year. Assuming that the distribution of speeding ticket costs is normally distributed and the population standard deviation is $13, is there sufficient evidence to support the police department’s claim at the 0.02 level of significance?arrow_forwardFran is training for her first marathon, and she wants to know if there is a significant difference between the mean number of miles run each week by group runners and individual runners who are training for marathons. She interviews 42 randomly selected people who train in groups and finds that they run a mean of 47.1 miles per week. Assume that the population standard deviation for group runners is known to be 4.4 miles per week. She also interviews a random sample of 47 people who train on their own and finds that they run a mean of 48.5 miles per week. Assume that the population standard deviation for people who run by themselves is 1.8 miles per week. Test the claim at the 0.01 level of significance. Let group runners training for marathons be Population 1 and let individual runners training for marathons be Population 2. Step 2 of 3 : Compute the value of the test statistic. Round your answer to two decimal places.arrow_forwardCitrus Rental is a popular car rental agency that has a history of having too few cars available, so that its available cars are overdriven. The mean monthly mileage over the years for Citrus cars has been about 1500 miles per month. Recently, though, Citrus purchased thousands of new cars, and the company claims that the average mileage of its cars is now less than in the past. To test this, a random sample of 11 recent mileages of Citrus cars was taken. The mean of these 11 mileages was 1332 miles per month, and the standard deviation was 232 miles per month. Assume that the population of recent monthly mileages of Citrus cars is normally distributed. At the 0.05 level of significance, can it be concluded that the mean recent monthly mileage, u, of Citrus cars is less than 1500 miles per month? Perform a one-tailed test. Then complete the parts below. Carry your intermediate computations to three or more decimal places and round your answers as specified in the table. (If necessary,…arrow_forward
- A clinical trial is planned to compare an experimental medication designed to lower blood pressure to a placebo. Before starting the trial, a pilot study is conducted involving eight participants. The objective of the study is to assess how systolic blood pressure changes over time untreated. Systolic blood pressures are measured at baseline and again 4 weeks later Is there a statistically significant difference in blood pressures over time? Run the test at a 5% level of significance. Give each of the following to receive full credit: 1) the appropriate null and alternative hypotheses; 2) the appropriate test; 3) the decision rule; 4) the calculation of the test statistic; and 5) your conclusion including a comparison to alpha or the critical value. You MUST show all your work to receive full credit. Partial credit is available. Baseline 4 weeks 135 136 150 142 143 135 160 158 152 155 143 140 133 128 146 129arrow_forwardAccording to the U.S. Department of Transportation’s Air Travel Consumer Report, the nation’s 12 largest airlines recorded an on-time arrival percentage of 77.4% in 2001. Of interest is to estimate the mean delay time for the 22.6% of all flights that did not arrive on time during 2013. A simple random sample of 28 late arriving flights was selected, and the mean delay time of this sample of 28 flights was 14.2 minutes, with a sample standard deviation of s= 6.4 minutes. Use this information to calculate and interpret a 98% confidence interval for the mean delay time for all flights that did not arrive on time during 2013.arrow_forwardA pharmaceutical company needs to know if its new cholesterol drug, Praxor, is effective at lowering cholesterol levels. It believes that people who take Praxor will average a greater decrease in cholesterol level than people taking a placebo. After the experiment is complete, the researchers find that the 44 participants in the treatment group lowered their cholesterol levels by a mean of 18.7 points with a standard deviation of 3.3 points. The 39 participants in the control group lowered their cholesterol levels by a mean of 18.1 points with a standard deviation of 2.1 points. Assume that the population variances are not equal and test the company’s claim at the 0.02 level. Let the treatment group be Population 1 and let the control group be Population 2. Step 1 of 3 : State the null and alternative hypotheses for the test. Fill in the blank below. H0: μ1=μ2 Ha : μ1⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯μ2 Step 2 of 3: what is the test statistic Step 3 of 3: draw a conclusion, fail or reject. Is…arrow_forward
- A large financial company employs a human resources mamanger who is in charge of employe benefits. The manger wishes to estimate the average dental expenses per employee for the company. She selects a random sample of 60 employee records for the past year and determines that the sample mean of $492. Moreover, it is known from past studies that the population standard deviation for annual dental expenses is $74. Use this data to calculate a 95% cofidence interval for the mean expenses of all employees.arrow_forwardA newly hired basketball coach promised a high- paced attack that will put more points on the board than the team's previously tepid offense historically managed. After a few months, the team owner looks at the data to test the coach's claim. He takes a sample of 36 of the team's games under the new coach and finds that they scored an average of 101 points with a standard deviation of 6 points. Over the past 10 years, the team had averaged 99 points. What is(are) the appropriate critical value(s) to test the new coach's claim at the 1% significance level? -2.438 -2.438 and 2.438 2.326 2.438arrow_forwardA team of researchers found that age distributions in a population of 100,000 people was not Normal. However, after they took a large number of simple random samples, each with (N=100), they observed that the sampling distribution of mean tended toward Normality. Really? Why is it possible?arrow_forward
- A coin-operated coffee machine made by BIG Corporation was designed to discharge a mean of 7.1 ounces of coffee per cup. If it dispenses more than that on average, the corporation may lose money, and if it dispenses less, the customers may complain. Believing that the mean amount of coffee dispensed by the machine, µ, is less than 7.1 ounces, BIG plans to do a statistical test of the claim that the machine is working as designed. Technicians gather a random sample of fill amounts and find that the mean of the sample is 6.7 ounces and that the standard deviation is 0.4 ounces. Based on this information, answer the questions below.arrow_forwardGary has discovered a new painting tool to help him in his work. If he can prove to himself that the painting tool reduces the amount of time it takes to paint a room, he has decided to invest in a tool for each of his helpers as well. From records of recent painting jobs that he completed before he got the new tool, Gary collected data for a random sample of 7 medium-sized rooms. He determined that the mean amount of time that it took him to paint each room was 3.4 hours with a standard deviation of 0.3 hours. For a random sample of 6 medium-sized rooms that he painted using the new tool, he found that it took him a mean of 3.2 hours to paint each room with a standard deviation of 0.2 hours. At the 0.05 level, can Gary conclude that his mean time for painting a medium-sized room without using the tool was greater than his mean time when using the tool? Assume that both populations are approximately normal and that the population variances are equal. Let painting times without using…arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





