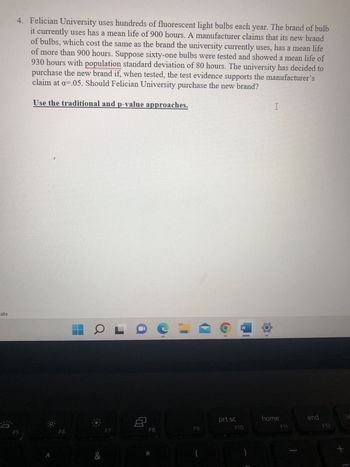
4. Felician University uses hundreds of fluorescent light bulbs each year. The brand of bulb it currently uses has a mean life of 900 hours. A manufacturer claims that its new brand of bulbs, which cost the same as the brand the university currently uses, has a mean life of more than 900 hours. Suppose sixty-one bulbs were tested and showed a mean life of 930 hours with population standard deviation of 80 hours. The university has decided to purchase the new brand if, when tested, the test evidence supports the manufacturer's claim at a=.05. Should Felician University purchase the new brand? Use the traditional and p-value approaches. I

A certain prescription medicine is supposed to contain an average of 250 parts per million (ppm) of a certain chemical. If the concentration is higher than this, the drug may cause harmful side effects; if it is lower, the drug may be ineffective. The manufacturer runs a check to see if the mean concentration in a large shipment conforms to the target level of 250 ppm or not. A simple random sample of 100 portions is tested, and the sample mean concentration is found to be 247 ppm. The sample concentration standard deviation is s = 12 ppm. Suppose that the p-value was 0.0259. What is the appropriate conclusion to make if α = 0.05? Group of answer choices Fail to reject H0. We have insufficient evidence to conclude that the mean concentration is different from 250 ppm. Fail to reject H0. We have sufficient evidence to conclude that the mean concentration is less than 250 ppm. Reject H0. We have insufficient evidence to conclude that the mean concentration is less than 250…

A professor believes that, for the introductory art history classes at his university, the mean test score of students in the evening classes is lower than the mean test score of students in the morning classes. He collects data from a random sample of 250 students in evening classes and finds that they have a mean test score of 88.1. He knows the population standard deviation for the evening classes to be 4.2 points. A random sample of 150 students from morning classes results in a mean test score of 89.1. He knows the population standard deviation for the morning classes to be 7.7 points. Test his claim with a 95 % level of confidence. Let students in the evening classes be Population 1 and let students in the morning classes be Population 2. Step 2 of 3: Compute the value of the test statistic. Round your answer to two decimal places.

Two popular brands of tires for tractor-trailers are the Puma and the Eternal. Salma is a buyer for a major shipping company and wants to determine if there is any difference between the two brands of tire in the mean distance (in thousands of km) driven on them before they need to be replaced. In the company's testing lab, Salma tests a random sample of 14 Puma tires and a random sample of 15 Eternal tires. (These samples are chosen independently.) For the Puma tires, the sample mean distance (in thousands of km) until they would need to be replaced is 54.71 with a sample variance of 5.95. For the Eternal tires, the sample mean distance (in km) until they would need to be replaced is 50.21 with a sample variance of 37.75. Assume that the two populations of distances driven are approximately normally distributed. Can Salma conclude, at the 0.05 level of significance, that there is a difference between the population mean of the distances (in thousands of km) driven on Puma tires before…

Suppose that the quarterly sales levels among health care information systems companies are approximately normally distributed with a mean of 12 million dollars and a standard deviation of 1.3 million dollars. One health care information systems company considers a quarter a "failure" if its sales level that quarter is in the bottom 20% of all quarterly sales levels. Determine the sales level (in millions of dollars) that is the cutoff between quarters that are considered "failures" by that company and quarters that are not. Carry your intermediate computations to at least four decimal places. Round your answer to one decimal place. million dollars X S

5. Old Faithful is a famous geyser at Yellowstone National Park. From a sample of 40 eruptions, the mean duration of Old Faithful eruptions is 3.7 minutes, and the standard deviation is 1.2 minutes. Find the percent of eruptions that have lasted from 1.3 minutes to 6.1 minutes.

4. A medical statistician wants to estimate the average weight loss of people who are on a new diet plan. In a preliminary study, he guesses that the standard deviation of weight loss is about 10 pounds. How large a sample should he take to estimate the mean weight loss to within 2 pounds, with a 90% confidence.

3. At a land farm, a farmer desired to test the effect of a given fertilizer on soybean production. He chose 24 plots of land of which are equal surface area. He treated 12 plots with the fertilizer and the others were untreated. Otherwise the conditions were the same. The treated plots produced soybean with mean yield 5.1 bushels and a standard deviation of 0.36 bushels, while the untreated plots had mean yield 4.8 bushels and a standard deviation of 0.40 bushels. (a) Can we conclude that there is a significant improvement in soybean production because of the fertilizer if a significance level of 1% is used? (b) What is the P-value of the test?

A mechanic sells a brand of automobile tire that has a life expectancy that is normally​ distributed, with a mean life of 34000 miles and a standard deviation of 2100 miles. He wants to give a guarantee for free replacement of tires that​ don't wear well. How should he word his guarantee if he is willing to replace approximately​ 10% of the​ tires?

A certain prescription medicine is supposed to contain an average of 250 parts per million (ppm) of a certain chemical. If the concentration is higher than this, the drug may cause harmful side effects; if it is lower, the drug may be ineffective. The manufacturer runs a check to see if the mean concentration in a large shipment conforms to the target level of 250 ppm or not. A simple random sample of 100 portions is tested, and the sample mean concentration is found to be 247 ppm. The sample concentration standard deviation is s = 12 ppm. What are the appropriate null and alternative hypotheses? Group of answer choices H 0:  x̄ = 250 vs. H a:  x̄ < 250 H 0:  x̄ = 250 vs. H a:  x̄ ≠ 250 H 0:  x̄ = 250 vs. H a:  x̄ > 250 H 0: μ = 250 vs. H a:μ < 250 H 0: μ = 250 vs. H a: μ ≠ 250 H 0: μ = 250 vs. H a: μ > 250