
College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
The Klein-Gordon equation at background level for a scalar field φ is given by
(found in image below)
where H is the Hubble parameter, V the potential of the scalar field, and V′ = dV/dφ.
Assume a flat Friedmann-Robertson-Walker universe, dominated by the scalar field.
i) State the conditions for slow-roll inflation. Write down the Friedmann equation and the
Klein-Gordon equation valid for slow-roll inflation.
ii) For a scalar field potential V =1/2m^2φ^2, where m is the mass of the field, calculate the
time evolution of the field φ in the case of slow-roll inflation.
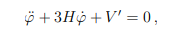
Transcribed Image Text:+3H +V' = 0,
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Suppose an alien race on a distant planet tries to send a message to us, with a laser (light). However, we were unaware that there is a stellar-mass black hole almost directly between us and them. How would this complicate our attempts to locate their position in the Galaxy? O Gravitational lensing would make the signal appear to be coming from a different location O The information carried by the laser (light) would be altered O It would not matter The black hole absorbs all of the lightarrow_forwardQ2 Draw a Feynman diagram for each of the reactions below. Clearly indicate all gauge bosons in your diagrams. (a) ve¯¯¯ + V₂ (b) y + y → µ³±µ˜¯arrow_forwardWith the aid of a diagram, explain the physical origin of cosmological redshift in an expanding universe, and how this differs from the Doppler shift due to relative motion. Observations of distantgalaxies indicate that their recession velocities, v, and their distances, d, follow a Hubble Law:v = H0d, where H0 is a constant. Using the analogy of an expanding grid or ruler, demonstratethat Hubble’s Law indicates that the Universe is undergoing uniform expansion.arrow_forward
- A survey that uses Type la supernovae as standard candles to measure the distances to galaxies, combined with spectroscopic analysis of those galaxies Select one: to obtain their redshifts and recession velocities, yields the data shown in the The Universe is undergoing а. table. Use the data to sketch a diagram of velocity versus distance. Choose the accelerated expansion statement given below that can be O b. The Universe is contracting. inferred from the data. Velocities and distances to Ос. The data does not provide sufficient galaxies information to determine the rate of Distance (Mpc) expansion of the Universe. Velocity (km/s) 10 730 d. The expansion rate of the Universe is 250 16250 constant 500 30000 e. The expansion of the Universe is 800 40000 decelerating. 1000 45000arrow_forwardSuppose that the universe were full of spherical objects, each of mass m and radius r, with the objects distributed uniformly throughout the universe as in the previous problem. (Assume nonrelativistic objects.) Given the density of these spherical objects (as you would have found in the previous problem), how far would you be able to see in meters, on average, before your line of sight intersected one of them? Values (note, different from the above problem): m = 3 kg r = 0.03 m Answer must be in scientific notation and include zero decimal places (1 sig fig).arrow_forwardOver the lifetime of the Universe, the dynamics of its expansion are dominated by the density of different constituents at different times. Ignoring expansion, what is the proper order for which constituent dominates from early to later times? Select one: a. First matter, then dark energy, then radiation b. First radiation, then matter, then dark energy c. First dark energy, then radiation, then matter d. First radiation, then dark energy, then matterarrow_forward
- Briefly explain what is meant by “particle horizon” and “event horizon” in cosmology. Calculate the physical particle horizon, RH(t), at time t. Assume a flat FRW universe whichis dominated by a fluid that gives rise to scale factor evolution where n is a constant with 0 < n < 1, and a(t0) = a0.arrow_forwardWhy does the cosmic microwave background (CMB) shine in low-energy microwave wavelengths? O The trapped photons within the plasma of the earliest universe originally had wavelengths in the microwave band due to rapid inflation O The CMB was originally emitted as high-energy gamma rays and x-rays, but the light has redshifted downward to lower-energy microwaves through time When nuclei of H and He first combined with free electrons to create atoms, photons of light were released as microwaves The photons released in the CMB were intensely hot, with energy levels in microwave wavelengths The early universe 380,000 years after the Big Bang was cold (2.7 kelvins) the temperature of microwave energyarrow_forwardWhat magnetic field B is needed to keep 943-GeV protons revolving in a circle of radius 1.0 km ? Use the relativistic mass. The proton's "rest mass" is 0.938 GeV/c². (1 GeV = 10⁹ eV) [Hint: In relativity, mrelv²/r = quB in still valid in a magnetic field, mrel = ym.] Express your answer to two significant figures and include the appropriate units B = μA Value Units ?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON

College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning

University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON

Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press

Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley

College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON