
ENGR.ECONOMIC ANALYSIS
14th Edition
ISBN: 9780190931919
Author: NEWNAN
Publisher: Oxford University Press
expand_more
expand_more
format_list_bulleted
Question
The figure below shows a consumer maximizing utility at two different prices (the left panel) and the consumer’s demand for good X at the same two prices of good X (the right panel). The price of good Y is $4.50. When the price of X increases from point S to point R along the demand curve, $_____ of income must be temporarily given to the consumer to isolate the substitution effect.
Multiple Choice $175 $180 $200 $360 $400
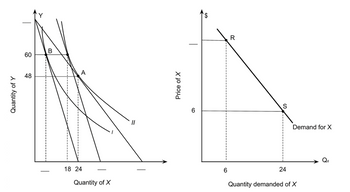
Transcribed Image Text:Quantity of Y
60
48
B
A
18 24
Quantity of X
11
Price of X
6
6
R
S
24
Demand for X
Quantity demanded of X
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, economics and related others by exploring similar questions and additional content below.Similar questions
- A consumer has an income of $400 and is deciding between two products: X and Y. Assume that the X product is the horizontal axis product. The price of X is $10 and the price of Y is $2. Assume the consumer currently wants to consume 50 units of product Y to maximize his utility. a) Write out the equation to this consumers budget line. What is the slope to this budget constraint? b) How much of X and Y will the consumer consume to maximize his utility subject to his budget constraint. C) Now assume the price of X changes to $5 and price of Y and Income stays the same. At the new price, the consumer wants to buy 60 units of product X to maximize her utility given her budget. How much X and Y will the consumer consume to maximize utility. g in the before and after the change of the budget constraint and indifference graph on the same graph space. Show all necessary points. Label clearly. ead oubstitutiofs. Draw d) Write out the expression of the utiiity maximizing ruie here.?arrow_forwardSuppose that U(f,c) = f + 8c^(1/2)is a utility function that describes Amelia’s preferences over two goods: fish(f)and custard (c). For the following, think of fish as the good graphed on the horizontal axis.a. Derive an expression for her marginal utility (Uf)from a small increase in f holding c fixed. Also find themarginal utility for custard (Uc).b. What is Amelia’s marginal rate of substitution (MRS)? Give a brief (2 sentences maximum) intuitivedescription of what MRS represents. If Amelia has 4 units of custard, holding her utility constant, howmany units of custard would she be willing to give up in order to get one more unit of fish?c. Graph Amelia’s indifference curve for a utility level of 40. Be sure to specify at least 3 bundles of goodson the indifference curve.d. Does the fact that Amelia’s indifference curve intersects with the custard axis violate any of the 5properties of indifference curves? Briefly support your answer.e. Give another utility function that represents…arrow_forwardEllie spends £20 on Energy drink (E) and Juice (J). Her preferences for these goods can be described by the following utility function: U ( E,J) = 2E + J^2 ( J squared) - J (MUt = 2, MUj = 2J - 1) Suppose that one energy drink costs £1.60 while one carton of Ellie’s favourite Juice costs £4.00. a) Find Ellie’s optimal consumption bundle. Provide both algebraic and graphical solution. Explain your reasoning. b) Discuss how Ellie’s optimal consumption choice would change when her disposable budget changes. c) If the price of energy drinks increases to £2.00 per can, how should the price of Juice change so that Ellie can be as well off as before this change in prices? d) Discuss the implications of the price change from c) on Ellie’s optimal choice. In your discussion, include the analysis of the substitution and income effects as well as Ellie’s demand for Energy drink and/or Juice.arrow_forward
- Alice receives an allowance of 500 dollars that she spends on buying snacks (S) and tea (T). The price of each snack is 10 dollars and the price of each tea is 5 dollars. Her utility is given by: U (S, T) = 2S³/4 +T3/4 (a) Find her marginal rate of substitution (MRS) between S and T. (b) Write Alice's budget constraint. (c) Find Alice's optimal consumption and the optimal A. (d) What is her new consumption if the price of tea becomes 10 dollars? Note: numeric solutions for questions (c) and (d) are not integers.arrow_forwardTrue, false, or undetermined?arrow_forwardUtility maximization with a budget constraint. A hypothetical consumer spends all tgheir income on ramen noodles (N) and wild rice (W). N is the quantity of noodles; W is the quantity of wild rice. Their income is $1,600 per month. the price of noodles is $2 per package and the price of wild rice is $20 per pound. The utility function is U=sqrt(N*W). the MRS = -N/W. The budget constraint is: 1,600 = 2*N + 20*W Graph Qty of noodles (N) on vertical axis and Qty of wild rice (W) on horizontal axis. SOLVE: a. Graph the budget constraint. label all points. What is the slope of the budget constraint? b. Find the optimal quantities of noodles(# of packages) and the wild rice (# of pounds) given the budget constraint. graph these optimal quantities. draw your indifference curve on the same graph. c. Show on your graph what happens when the price of wild rice increases to $40 per pound. Find your new optimal quantities of noodles and wild rice. label all points on graph. label the…arrow_forward
- Gino derives utility from only two goods, carrots (Qc) and donuts (Qd). His utility function is as follows:U(Qc,Qd) = (Qc)(Qd)The marginal utility that Donald receives from carrots (MUc) and donuts (MUd) are given as follows:MUc = Qd MUd = QcGino has an income (I) of £120 and the price of carrots (Pc) and donuts (Pd) are both £1. - suppose a lump sum tax of the same dollar amount, of a 1 pound tax per unit on donuts, is levied on Gino. what is Gino's utility maximising market basket? - why would Gino prefer a per unit tax over the lump sum tax, or vice versa, or why is he indifferent between the two taxes.arrow_forward6.arrow_forwardJohn has $300 as income and he uses his income only for apples and bananas. If he uses his income only for apples, he can buy 10 pounds. If he uses his income only for bananas, he can buy 15 pounds. Which one is the correct formula for his budget constraint when X=pounds of apples, Y=pounds of bananas and the prices are per pound? a) More information is needed to answer the question. b) 15X + 10Y = 300 c) 10X + 15Y = 300 d) 20X + 30Y = 300 e) 30X + 20Y = 300arrow_forward
- Gino derives utility from only two goods, carrots (Qc) and donuts (Qd). His utility function is as follows:U(Qc,Qd) = (Qc)(Qd)The marginal utility that Donald receives from carrots (MUc) and donuts (MUd) are given as follows:MUc = Qd MUd = QcGino has an income (I) of £120 and the price of carrots (Pc) and donuts (Pd) are both £1. - what is Gino's budget line and what quantities of Qc and Qd will maximise Gino's utitlity? - holding income and Pd constant, what is Gino's demand curve for carrots? - suppose a tax of 1 pound per unit is levied on donuts. how will this alter Gino's utility maximisinzing market basket of goods?arrow_forwardA consumer currently spends a given budget on two goods, X and Y, in such quantities that the marginal utility of X is 15 and the marginal utility of Y is 8. The unit price of X is $3 and the unit price of Y is $2. The utility-maximizing rule suggests that this consumer should Multiple Choice a. decrease consumption of product X and increase consumption of product Y. b. increase consumption of product X and increase consumption of product Y. c. decrease consumption of product Y and increase consumption of product X. d. stick with the current consumption mix because it yields maximum utility.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you

 Principles of Economics (12th Edition)EconomicsISBN:9780134078779Author:Karl E. Case, Ray C. Fair, Sharon E. OsterPublisher:PEARSON
Principles of Economics (12th Edition)EconomicsISBN:9780134078779Author:Karl E. Case, Ray C. Fair, Sharon E. OsterPublisher:PEARSON Engineering Economy (17th Edition)EconomicsISBN:9780134870069Author:William G. Sullivan, Elin M. Wicks, C. Patrick KoellingPublisher:PEARSON
Engineering Economy (17th Edition)EconomicsISBN:9780134870069Author:William G. Sullivan, Elin M. Wicks, C. Patrick KoellingPublisher:PEARSON Principles of Economics (MindTap Course List)EconomicsISBN:9781305585126Author:N. Gregory MankiwPublisher:Cengage Learning
Principles of Economics (MindTap Course List)EconomicsISBN:9781305585126Author:N. Gregory MankiwPublisher:Cengage Learning Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning
Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning Managerial Economics & Business Strategy (Mcgraw-...EconomicsISBN:9781259290619Author:Michael Baye, Jeff PrincePublisher:McGraw-Hill Education
Managerial Economics & Business Strategy (Mcgraw-...EconomicsISBN:9781259290619Author:Michael Baye, Jeff PrincePublisher:McGraw-Hill Education


Principles of Economics (12th Edition)
Economics
ISBN:9780134078779
Author:Karl E. Case, Ray C. Fair, Sharon E. Oster
Publisher:PEARSON

Engineering Economy (17th Edition)
Economics
ISBN:9780134870069
Author:William G. Sullivan, Elin M. Wicks, C. Patrick Koelling
Publisher:PEARSON

Principles of Economics (MindTap Course List)
Economics
ISBN:9781305585126
Author:N. Gregory Mankiw
Publisher:Cengage Learning

Managerial Economics: A Problem Solving Approach
Economics
ISBN:9781337106665
Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike Shor
Publisher:Cengage Learning

Managerial Economics & Business Strategy (Mcgraw-...
Economics
ISBN:9781259290619
Author:Michael Baye, Jeff Prince
Publisher:McGraw-Hill Education