Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: What is the CONTRAPOSITIVE of the statement p q ? O q p d--b- O Op--
A:
Q: Can you help me with this discreet math problem:
A: 1. Converse: Swaps the hypothesis and the conclusion  The converse of "If n is at least 2, then n²…
Q: Is it okay if I say "not all cookies are baking?" I think I have to have the word "not" in my andwer
A: To write the negation of Some cookies are baking.The negation of word ''some'' is ''not all''.
Q: For the given fact below, which subsequent true/false statement is true?   Fact: Mel received in A…
A:
Q: For the simple statements p: There is a fire in the fireplace. q: The house is cold. Match each…
A: There is no fire in the fireplace if and only if the house is cold. There is no fire in the…
Q: Write the negation of the statement. Start the negation with the word "Some," "No," or "All." No…
A: Negation of a statement: If P is a statement, then the negation of the statement P denoted by ~P is…
Q: The winner of the reality show will either meet the vice president or the president. We know she…
A: Note: We are required to answer only the first question, unless specified.  Disjunctive Syllogism:…
Q: 4b. In the following exercises I give you the symbols that you will use for predicates or relations.…
A: Asper the guidelines I’m supposed to solve only three subparts of the given problem: Given that: (i)…
Q: P₁ then q" 8. (a) Write each of the following statements, in English, in the form "if (i) In order…
A: The objective of the question is to translate the given statements into 'if' form, prepare a truth…
Q: Consider the given statement. If it is not spring, then we are not going swimming. For each…
A: Given statement, If it is not spring, then we are not going swimming. The objective is  to determine…
Q: 2. Write down the negation of the following statements: I study both algebra and geography. I do not…
A:
Q: (c) Write down two simple statements A and B. (They should be statements whose truth value can be…
A: (c) Consider the following statements : A : 2 is even  B : apple is a fruit Both of these statements…
Q: Use the five sentences below to answer the question. Mark had told him about the foxes. John looked…
A: In this question we have to how many different five sentence paragraphs can be formed if the…
Q: Use the fact that -(p+q) is equivalent to p A-q to write the statement in an equivalent form. It is…
A: Here we define the p and q explicitly. Then apply the given operation.
Q: The topic is on math logic • examle. There is exactly one student. The logical structure of this…
A: We have to convert the given statement "There are exactly two students" in to corresponding logical…
Q: Negate the following statement and give your answer as an English-language sentence. 3e € Z | Vn Z,…
A:
Q: 3. We want to find S so ((A = B) A B) = S is a tautology. A B(A→ B) ^ B TT TF FT S ((A = B) ^ B) = S…
A:
Q: An argument is expressed in English below. Lachlan is tired or Lachlan is not surprised. Lachlan is…
A: Lachlan is tired or Lachlan is not surprised. Lachlan is joyful.
Q: 4d. In the following exercises I give you the symbols that you will use for predicates or relations.…
A: (iv) Only white swans exist.          ≡ Every swan is white.          ≡ ∀x (Sx → Wx)
Q: Open with 3. All of the employees at the AcmeSoft company are either programmers or salespeople. The…
A:
Q: 2. We want to find S so ((A → B) ^ A) = S is a tautology. AB(A→B) A A TT TF FT FF S ((A→ B) ^ A) =>…
A: A proposition of the form “if p then q” or “p implies q”, represented “p => q” is called a…
Q: Choose the numbers that are counterexamples for the O 3,8 O 4,6 0 1,7 0 2,-1
A: To choose a counter example
Q: VERBAL IF-THEN'S For each of the following, do your best to figure out if the statement is true or…
A: According to company rules we can answer only first three sub parts and rest can be reposted
Q: Select the negation of All movies are too long. Some movies are not too long. Some movies are too…
A: Here we want to know the negative for te given statement.
Q: Which of the following statements are correct if yi =2xi ∀i = 1, 2, ....., n? A. y = 2x B. y = 4x…
A: we have to find the right function
Question

I need help with the explanation for how to find if True or False and why...

For the first 3 statements I'm unsure how to check or understand why they are true or false but I believe the the following for them is 50 T, 51 T (If P false and Q false then True... don't understand why P is false in this case though...), 52 T

For Negations, Converse and Contrapositives how do I know if they are true or not? 

Is it if Original in True then Negation is False? If Original True Contrapositive True? What about Converse?

**Question 50**: For all natural numbers \( a \), \( a^2 \equiv 0 \pmod{4} \) or \( a^2 \equiv 1 \pmod{4} \). **Question 51**: For all natural numbers \( a \), if \( a^2 \equiv 2 \pmod{4} \), then \( 1 = 2 \). **Question 52**: For all natural numbers \( a \), if \( a^2 \equiv 2 \pmod{4} \), then \( 1 \neq 2 \). **Question 53**: The negation of #51 is true. **Question 54**: The negation of #52 is true. **Question 55**: The converse of #51 is true. **Question 56**: The converse of #52 is true. **Question 57**: The contrapositive of #51 is true. **Question 58**: The contrapositive of #52 is true. **Question 59**: The contrapositive of #52 is true.
expand button
Transcribed Image Text:**Question 50**: For all natural numbers \( a \), \( a^2 \equiv 0 \pmod{4} \) or \( a^2 \equiv 1 \pmod{4} \). **Question 51**: For all natural numbers \( a \), if \( a^2 \equiv 2 \pmod{4} \), then \( 1 = 2 \). **Question 52**: For all natural numbers \( a \), if \( a^2 \equiv 2 \pmod{4} \), then \( 1 \neq 2 \). **Question 53**: The negation of #51 is true. **Question 54**: The negation of #52 is true. **Question 55**: The converse of #51 is true. **Question 56**: The converse of #52 is true. **Question 57**: The contrapositive of #51 is true. **Question 58**: The contrapositive of #52 is true. **Question 59**: The contrapositive of #52 is true.
Expert Solution
Check Mark
Step 1: Part 50

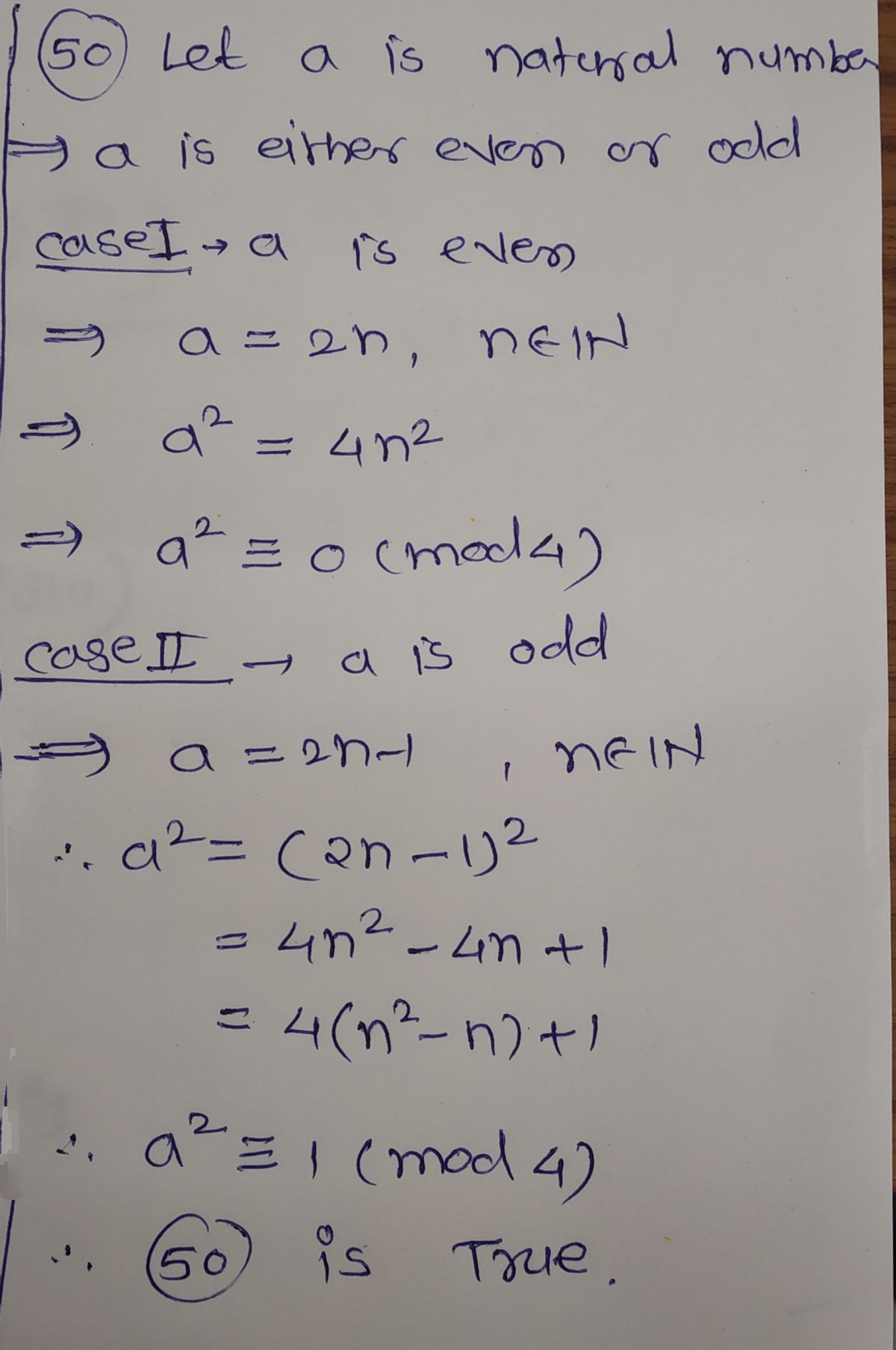
Advanced Math homework question answer, step 1, image 1

bartleby

Step by stepSolved in 5 steps with 5 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS