Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
I understand almost all of this. The part I am stuck on is how do you figure out what to make your statements. I need to know what statement to use for P and what one to use for Q. Ive noticed certain problems they are opposite of what the bold sentence says.
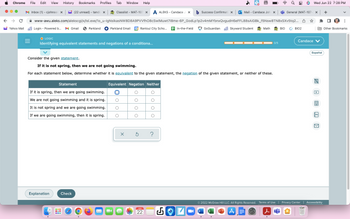
Transcribed Image Text:---
### Identifying Equivalent Statements and Negations of a Conditional
#### Consider the given statement:
**If it is not spring, then we are not going swimming.**
For each statement below, determine whether it is **equivalent** to the given statement, the **negation** of the given statement, or **neither** of these.
| **Statement** | **Equivalent** | **Negation** | **Neither** |
|-------------------------------------------------------|----------------|--------------|-------------|
| If it is spring, then we are going swimming. | ⭘ | ⭘ | ⭘ |
| We are not going swimming and it is spring. | ⭘ | ⭘ | ⭘ |
| It is not spring and we are going swimming. | ⭘ | ⭘ | ⭘ |
| If we are going swimming, then it is spring. | ⭘ | ⭘ | ⭘ |
Click the "Explanation" button for detailed information regarding the solution.
To submit your answer, click the "Check" button.
#### Diagram Explanation:
This table provides a structured overview to assess the logical relationships between different conditional statements. Each row presents a statement that needs to be analyzed, and the columns allow you to categorize the statement as "Equivalent," "Negation," or "Neither" relative to the original statement.
If you need further clarification or have questions, please use the "Explanation" or help icons provided on the interface.
© 2022 McGraw Hill LLC. All Rights Reserved.
---
This page is designed to help students understand logical equivalence and negation in conditional statements through an interactive table.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 6 steps
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Thank you so much! So when i make my new p and q statements to start the problem do i make both of those trues so in other words they wouldnt have the words "not spring" " not swim"
Solution
by Bartleby Expert
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Thank you so much! So when i make my new p and q statements to start the problem do i make both of those trues so in other words they wouldnt have the words "not spring" " not swim"
Solution
by Bartleby Expert
Knowledge Booster
Similar questions
- The median yearly salary paid to the 24 players on a soccer team is $24,000 less than the median yearly salary paid to the 12 players on a basketball team. Based on this information, which of the following statements must be true? a The highest-paid soccer player earns more than the lowest-paid basketball player. All 12 players on the basketball team earn more than each player on the soccer team. At least one of the basketball players ears exactly $24,000 more than one of the soccer players. The 6 highest-paid basketball players each earn more than each of the 12 lowest-paid soccer players.arrow_forwardVERBAL IF-THEN'S For each of the following, do your best to figure out if the statement is true or false. Give an explanation (or argument) justifying why you think what you think. NOTE: Each of the following refers to "a number" or “numbers". They are general statements. So, if there is any number (or numbers) for which it's false, then the statement is false. In other words, if you are thinking "that's true in some cases (or perhaps even many cases), but it's not true in all cases," then the statement is false. Warning: The word "number" does not mean "integer" or "positive integer". All integers are numbers, but not all numbers are integers. Integers are numbers like -13, -4, 0, 27, and 132. Non-integers are numbers like 2.61, - 5.8, and 55/9. The first of these is between the consecutive integers 2 and 3. The second is between -6 and -5. The third is between 6 and 7. So if you are going to test the statements by choosing a number or numbers to test it with, do not limit yourself to…arrow_forwardWhat is the value of the following statement ? Let a ₁ = −2, a 2 = −1, a3 =0, a 4 = 1, and a5 = 2 1 2 -1 0 -2 2 k = 1 a 2 karrow_forward
- beautiful, wore, contest, a, Margot, to, the, pie-eating hat Margot a beautiful hat wore a to the pie-eating contest. Margot the pie-eating contest wore a beautiful hat. Margot wore a beautiful hat to the pie-eating contest.arrow_forwardWhich type of reasoning is illustrated below?. Because it has rained the previous four days, Annie concludes that it will rain again today.arrow_forward6) Mr. Munson, the art teacher, is organizing his supplies for his students' upcoming art project. He has 65 markers and 52 crayons. He wants to put the markers and crayons into containers for each table group so that there are the same number of markers and the same number of crayons in each container. Part A: Write an expression using the distributive property to show how the marks and crayons are distributed such that Mr. Munson can make the largest number of containers. Part B: What is the largest number of tables he can make and how many of each supply will be at each table?arrow_forward
- Decide whether each of the following statements makes sense (or is clearly true) or does not make sense (or is clearly false). Explain your reasoning.arrow_forwardGlenn and Kim are members of a comedy troupe that has 10 members in all. How many ways can the 10 members line up if Glenn and Kim must stand side by side? Give the expression that can be used to calculate the number of ways the members of the troupe can line up. Choose the correct answer below. O A. 8!.9.2 B. 10! 2 O C. 8! 8! 2 O E. 10!.9 O G. 81.9 The number of ways that the troupe can line up is (Simplify your answer.) O D. O F. 10! O H. 10!.9.2arrow_forwardI have a permutations & combinations geometry question.arrow_forward
- For the given fact below which subsequent true/false statement is true? Fact : Mel received in A in math Mel passes the math class? Mel likes math?arrow_forwardAn educational psychologist develops a new math program she believes will accelerate arithmetic skills in a population of at-risk students in 2nd grade. The researcher decides to determine if the sample’s scores on an arithmetic test exceeded the population average for at-risk math students. a. Formulate a H0 and a H1 for a non-directional test using BOTH symbols and words. b. Formulate a H0 and a H1 for a directional test using BOTH symbols and words.arrow_forwardUse the following information to answer the next question Leonidas is having a party and is planning to play some great music over the dinner hour. He made a short list of 18 songs that include 10 classical songs and 8 jazz songs. Over the dinner hour it is decided that of the 18 songs, 4 classical songs and 3 jazz songs will be selected, and then arranged into an order to be played. To determine the number of potential music arrangements for the party the following expressions were created: i) 10C4 X 8C3 X 7! ii) 10P4 8P3 iii) (¹0)(3) × 5040 iv) 18P7 v) (10 x 9 x 8 x 7) × (8 × 7 × 6) vi) 11. How many of the above expressions are correct? a) 5 b) 4 (10x9x8x7) (8x7x6) X 4! 3! c) 3 x 7! d) 2arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,