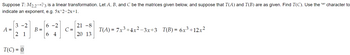
Suppose T: M2,2→P3 is a linear transformation. Let A, B, and C be the matrices given below, and suppose that T(A) and T(B) are as given. Find T(C). Use the character to indicate an exponent, e.g. 5x^2-2x+1. A = 3-2 2 1 T(C) = 0 B = 6-2 64 C= 21-8 20 13 T(A) = 7x³+4x²-3x+3 T(B) = 6x³ +12x²

Find the final amount of money in an account if $8,100 is deposited at 6.5% interest compounded quarterly every 3 months and the money is left for 5 years

1. Consider the matrices 2 -2 A₁ - (₁ 3)₁ 4₂ = (3-2), A₁ = ( −² −2 ). -(13), , 1 0 -2 (a) and A4 These matrices can be used to build functions 2TA₁, A₂, A3z, and at A4z. These functions are represented (in an arbitrary order) in Figure 1. Match each matrix with its corresponding picture. Explain briefly. -5 -4 -(-6). (b) (c) Figure 1: Graphical representation of functions (d)

Let f and g be the linear transformations represented by the matrices (2-1) and (3-3), -5 -4 respectively. What is the image of the point (-1, 1) under the composite transformation go f? O (-4,1) O (-14, 25) O (-12, 6) O(-4,0) O (-15, 24)