Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: 1 1 2 d the solution to the linear system of differential equations [1] = sfying the initial…
A:
Q: Suppose that all the eigenvalues of the matrix A have negative real part. Then every solution of the…
A: Consider the provided question, Suppose that all the eigenvalues of the matrix A have negative real…
Q: Consider the linear system Find the eigenvalues and eigenvectors for the coefficient matrix. A₁ = 15…
A: For given system,                   the coefficient matrix is         To find eigenvalues of ,…
Q: The eigenvalues of the coefficient matrix can be found by inspection or factoring. Apply the…
A:
Q: Use the eigenvalue and Method to find the general eigen vector solution of the following finst onden…
A:
Q: The eigenvalues of the coefficient matrix can be found by inspection or factoring. Apply the…
A: Given system is x1'=6x1+5x2+5x3, x2'=-7x1-6x2-5x3, x3'=7x1+7x2+6x3   To Find: Eigenvalues and then…
Q: The eigenvalues of the coefficient matrix can be found by inspection or factoring. Apply the…
A:
Q: 2. x' = Find the general solution of the system of equations. -20 28 8 -14 22 4 X -21 21 14
A: Find: the general solution of the system of equations. x'=-20288-14224-212114x
Q: = eat. Use 4. Consider the equation x" - 2ax' + a²x = 0, which has solution x = reduction of order…
A:
Q: Apply the eigenvalue method to find a general solution of the given system. Use a computer system…
A:
Q: Describe the overall process for solving a system of linear differential equations using the…
A: We have give the overall process for solving a system of linear differential equations using the…
Q: Suppose the size of a population evolves according to the logistic equa- tion: dN = 1.5N dt N 100…
A:
Q: The eigenvalues associated with the equation below are all nonnegative. y" + λy = 0; y'(−π) = 0,…
A: As per the question, we are asked with exploring the eigenvalues and eigenfunctions of a…
Q: 6. Solve the initial value problem. Express your solution as a single vector. 2-(33) ², 2(0) - (1) =…
A:
Q: B.X2 = 4x₁ + 6x₂ + 4x3, X'3 = 5x₁ +4x2 +5x3 tion in matrix form? ...
A:
Q: 1. Find the general solution of the system of equations. x² = ( 3 3 ) = x'
A: To Find: the general solution of the system of equations. x'=7-55-3x
Q: Consider the initial value problem 70) - -6 1 -6 a. Find the eigenvalue A, an eigenvector õ, and a…
A: This is a matrix of a type with repeated eigen value.
Q: For the system of differential equations, = A₁, A₂ = U₁ = U2 = y' a) Find the characteristic…
A:
Q: Consider the system of linear differential equations: X = AX. (i) Suppose is an eigen value of A of…
A: A generalized eigenvector of a matrix A corresponding to an eigenvalue λ is a nonzero vector x that…
Q: The eigenvalues of the coefficient matrix can be found by inspection or factoring. Apply the…
A: Let us consider system of differential equation: X'=AX Find the eigenvalues of matrix A. let us say…
Q: None
A: To find the eigenvalues and eigenfunctions for the differential equation:y'' - 2y' + (1 + lambda)y =…
Q: Use Eigenvalue method to find the solution of the given linear system: x' = 6x - 4y, y' = x + 2y,…
A:
Q: Find eigenvalues associated with this system of differential equations. X. -2 -1 and -2 -2 and -3 O…
A:
Q: Consider the initial value problem (a) Find the eigenvalues and eigenvectors for the coefficient…
A:
Q: The eigenvalues of the coefficient matrix can be found by inspection or factoring. Apply the…
A:
Q: Consider the following system of linear differential equations: dx dt dy dt (a) Find the eigenvalues…
A: Since there are multiple subparts, so according to Bartleby guidelines I will solve only 1st 3 sub…
Q: Find the values of such that the equations have non-trivial solutions. What are the eigenvalues and…
A:
Q: 2 10 3. Let B = 1 2 0 0 0 1 (a) Show that A = 1 is an eigenvalue of B of multiplicity 2. Find…
A:
Q: One solution of t + 2 t =x² + t + 2 is x₁ (t) = t. Find a second independent X1 - x = 0 t² solution.
A:
Q: Find all solutions of the following system of linear equations: dx dt = = 4x + 8y, Xg dy dt = Hi, I…
A:
Q: Please help solve for my homework
A: Step 1: Step 2: Step 3: Step 4:
Question
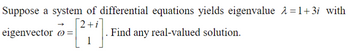
Suppose a system of differential equations yields eigenvalue λ=1+3i with 2+i eigenvector = Find any real-valued solution.
expand button
Transcribed Image Text:Suppose a system of differential equations yields eigenvalue λ=1+3i with 2+i eigenvector = Find any real-valued solution.
Expert Solution
Check Mark
Step 1: Determine the given variables

Given space that The space eigen space value space space straight lambda subscript 1 equals 1 plus 3 i space This space is space in space the space form space lambda subscript 1 equals alpha plus beta i Here space space alpha equals 1 space space comma space space beta equals 3 The space eigenvector space omega with rightwards arrow on top equals open square brackets table row cell 2 plus i end cell row 1 end table close square brackets equals open square brackets table row 2 row 1 end table close square brackets plus straight i open square brackets table row 1 row 0 end table close square brackets This space is space in space the space form space omega with rightwards arrow on top equals u subscript 1 plus i u subscript 2 Here space space u subscript 1 equals open square brackets table row 2 row 1 end table close square brackets space space comma space space u subscript 2 equals open square brackets table row 1 row 0 end table close square brackets

bartleby

Step by stepSolved in 3 steps with 3 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS