Bartleby Related Questions Icon

Related questions

Q: Think of our Milky Way Galaxy as a flat circular disk of diameter 100,000 light-years. Suppose we…
A: There are many units to calculate length. Bigger units like astronomical unit, parsec, etc are used…
Q: Use the small angle equation to find the angular diameter of Sgr A* if it has a diameter of 13 AU…
A: The small-angle equation is used in astronomy to calculate the distance between Earth and other…
Q: Using the differential equation model: (dN/dt) = - kN. (k>0) where N(t) = amount of 14C at time t,…
A:
Q: What is the wavelength shift (delta) (h) of a exoplanetery system at a wavelength of X angstroms if…
A: The Doppler shift is a change in frequency or wavelength of a wave in relation to an observer who is…
Q: MXCRA An object initially at rest accelerates uniformly and travels 26.399_m during its first…
A:
Q: A charged particle moving through a magnetic field at right angles to the field with a speed of 23.7…
A: Given data: The speed of charge particle is v=23.7 m/s. The magnetic force is F=2.98x10-4 N. The…
Q: What is advection dominated accretion flow in balck holes?
A: In a binary system of a black hole and a star, the black hole will start absorbing the mass from the…
Q: Given that an astronomical unit is 1.5x10° kilometers and a light-year is about 1013 kilometers, how…
A: The distance between Sun and Earth is defined as the Astronomical Unit (AU). It was created by…
Q: If Sirius were moved 10x further away what would happen to its: parallax, surface temperature,…
A: **As per our company guidelines we are supposed to solve only one question (if there are multiple…
Q: The Swe solid epheres A o B have aeame emissirity. ovadius of À is four times the gradius of 8 @g…
A: Solution : Let RA & RB be the radii of sphere A & B respectively. TA & TB be their…
Q: Suppose you gathered a ball of interstellar gas that was equal to the size of the Earth (a radius of…
A:
Q: Question: Record the angular shift. 1.7 arcsec Question: These images were taken six months apart,…
A:
Q: Every star has certain properties that help to define it. Some of the main properties of stars are:…
A:
Q: Determine the erosion depth per year of a Mylar film placed in the outer surface of a spacecraft…
A: The erosion yield of Mylar film is given 2.3×10-24 cm3/ Oxygen atomThe average atomic-oxygen number…
Q: A sample from a meteorite that landed on Earth has been analyzed, and the results shows that out of…
A:
Q: Astronomy) Cygnus Loop Velocity. If the Cygnus Loop is 25 pc in diameter and is 10,000 years old,…
A:
Q: The total electric field consists of the vector sum of two parts. One part has a magnitude of E₁ =…
A:
Q: Tn Course: SUNO - 2020 FALL - Mair X WA Test 1- SPHY 213N General Phys X…
A: since you have posted a question with multiple subparts, we will solve first three subparts for you.…
Q: A distant galaxy has an apparent magnitude of 13 and is 5,000 kpc away. What is its absolute…
A: Apparent Magnitude The apparent magnitude of a star or a galaxy is the measure of how bright the…
Q: An object's position is given by x = 09 m/s, 9 m/s -3 m/s, 3 m/s -6 m/s, 6 m/s O-10 m/s, 10 m/s 5 -…
A:
Q: Where did the values for (T - 20 C) come from?
A:
Q: Just need help with 22-2. Thank you!
A: Formula of Coulomb force is as follows: Fe=kq2d2…
Q: The time it takes for a cloud 106,000 AU in radius to collapse in "free-fall to form a new star is…
A:
Q: Next you will (1) convert your measurement of the semi-major axis from arcseconds to AU, (2) convert…
A:
Q: describe in detail why and in what situation you use mgh=1/2kx^2, and the question (why it is…
A: mgh = (1/2) kx2 where m is the mass g is the acceleration due to gravity h is the maximum height k…
Question

Need help understanding where the term 1/5mR^2Φ^2 came from in the Lagrangian

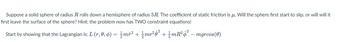
Suppose a solid sphere of radius R rolls down a hemisphere of radius 5R. The coefficient of static friction is u. Will the sphere first start to slip, or will will it first leave the surface of the sphere? Hint: the problem now has TWO constraint equations! Start by showing that the Lagrangian is: L (r, 0, 6) = {{mr² + ½{mr²0² + {{mR² $² – mgrcos(0)
expand button
Transcribed Image Text:Suppose a solid sphere of radius R rolls down a hemisphere of radius 5R. The coefficient of static friction is u. Will the sphere first start to slip, or will will it first leave the surface of the sphere? Hint: the problem now has TWO constraint equations! Start by showing that the Lagrangian is: L (r, 0, 6) = {{mr² + ½{mr²0² + {{mR² $² – mgrcos(0)
Expert Solution
Check Mark
Step 1

Lagrangian: 

Lagrangian for the motion of a particle is defined by the equation,

L=K-U                                                                  (1)

where K is the total kinetic energy of the particle and U is the total potential energy of the particle.

 

bartleby

Trending nowThis is a popular solution!

bartleby

Step by stepSolved in 4 steps with 1 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions