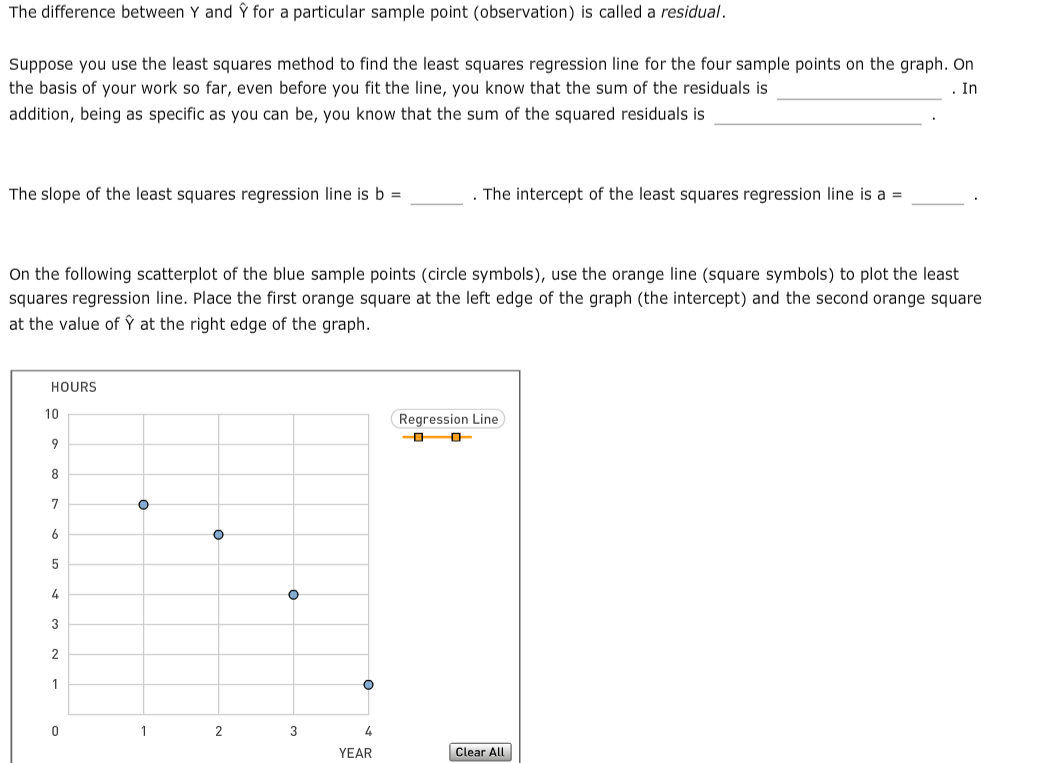
Student Year in College Course Work Hours per ClassFreshman (1)2Sophomore (2)3Junior (3)44Senior (4)A scatterplot of the sample data follows [blue points (circle symbols)]. The line Y = 8 - X is alsoHOURS10O Sum of Distances8 0(x-bar, y-bar))х5YEARClear All2.2. The difference between Y and Ỹ for a particular sample point (observation) is called a residual.Suppose you use the least squares method to find the least squares regression line for the four sample points on the graph. Onthe basis of your work so far, even before you fit the line, you know that the sum of the residuals is. Inaddition, being as specific as you can be, you know that the sum of the squared residuals isThe slope of the least squares regression line is b =. The intercept of the least squares regression line is a =On the following scatterplot of the blue sample points (circle symbols), use the orange line (square symbols) to plot the leastsquares regression line. Place the first orange square at the left edge of the graph (the intercept) and the second orange squareat the value of Ý at the right edge of the graph.HOURS10Regression Line3134.YEARClear All

Answered: Image /qna-images/answer/356c1128-8143-4e6a-bdff-3621aa118486.jpg

Answered: Student Year in College Course Work…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Similar questions

12:57 K An engineer wants to determine how the weight of a gas-powered car, x, affects gas mileage, y. The accompanying data represent the weights of various domestic cars and their miles per gallon in the city for the most recent model year. Complete parts (a) through (d) below. Click here to view the weight and gas mileage data. (a) Find the least-squares regression line treating weight as the explanatory variable and miles per gallon as the response variable. Car Weight and MPG y=x+ (Round the x coefficient to five decimal places as needed. Round the constant to two decimal places as needed.) ||| = Weight (pounds), x 3670 3880 2687 3623 3382 2884 3734 2683 3532 3877 3223 Print Miles per Gallon, y SANONNINGHE 16 17 24 19 22 22 17 24 20 16 Vo) 1 LTE2 + ... ... 18 Done 43% O X
The estimated regression line: a. does not change the sum of squared residuals.b. maximizes the sum of squared residuals.c. minimizes the sum of squared residuals.d. sometimes maximizes and sometimes minimizes the sum of squared residuals.can you also explain the answer, please
Answer the following: 2. Describe the form, direction, and strength of the relationship between these variables. Does there appear to be any outliers? 3. The equation of least-squares regression line is y = 6.871 + 0.061x. This line goes through the points (0, 6.9) and (700, 49.5). Use these points to add the regression line to your scatterplot above. 4. One animal is farthest from the regression line and is an outlier for these two variables. Find the name of this animal and write a sentence describing how its position differs from the overall relationship among the other animals. 5. The elephant has the longest gestation period of these animals. a. Considering only the gestation variable, would you say that the elephant is an outlier? Write a sentence or two explaining why or why not? b. Considering both variables and the relationship between average life span and average gestation period, would you say the elephant is an outlier now? Write a sentence or two explaining why or why…
A medical experiment on tumor growth gives the following data table. X: 65, 70, 86, 100, 222. Y: 33, 35, 45, 52, 70. The least squares regression line was found. Using technology, it is determined that the total sum of squares (SST) was 898 and the sum of squares of regression (SSR) was 806.2. Calculate R2, rounded to three decimal places
Consider the set of points (0,9),(1,5),(6,3) and (9,2). In this set of points, the age of a dolphin is the first part of each ordered pair and the second part is the number of tricks that the dolphin learned in a month. So, the 6 year-old dolphin learned 3 tricks in the month. Write the least squares regression line for this data. Use the line to estimate how many tricks a 4 year-old dolphin could learn. Then find r and r2. Explain what r2 means.
An engineer wants to determine how the weight of a gas-powered car, x, affects gas mileage, y. The accompanying data represent the weights of various domestic cars and their miles per gallon in the city for the most recent model year. Complete parts (a) through (d) below. (a) Find the least-squares regression line treating weight as the explanatory variable and miles per gallon as the response variable. y=nothingx+(nothing) (Round the x coefficient to five decimal places as needed. Round the constant to one decimal place as needed.) (b) Interpret the slope and y-intercept, if appropriate. Choose the correct answer below and fill in any answer boxes in your choice. (Use the answer from part a to find this answer.) A. A weightless car will get nothing miles per gallon, on average. It is not appropriate to interpret the slope. B. For every pound added to the weight of the car, gas mileage in the city will decrease by nothing mile(s) per gallon, on…
Might we be able to predict life expectancies from birthrates? Below are bivariate data giving birthrate and life expectancy information for each of twelve countries. For each of the countries, both x, the number of births per one thousand people in the population, and y, the female life expectancy (in years), are given. Also shown are the scatter plot for the data and the least-squares regression line. The equation for this line is y=82.25 -0.48x. ^ Birthrate, x (number of births per 1000 people) 35.5 44.9 29.7 19.9 13.7 27.0 51.9 15.0 50.9 49.7 39.6 24.4 Send data to calculator Send data to Excel Female life expectancy, y (in years) 67.9 57.9 61.7 71.4 72.5 73.5 55.4 76.5 58.2 60.6 64.4 74.4 Based on the sample data and the regression line, complete the following. Female life expectancy (in years) 85 80+ 75+ 70- 65+ 60- 55+ 50 x X x ++ 10 15 20 25 (b) According to the regression equation, for an increase of one (birth per 1000 people) in birthrate, there is a corresponding decrease…
estion 7 of 15 Suppose the manager of a gas station monitors how many bags of ice he sells daily along with recording the highest temperature each day during the summer. The data are plotted with temperature, in degrees Fahrenheit (°F), as the explanatory variable and the number of ice bags sold on as the response variable. The least squares regression (LSR) line for the data is y = -114.05 +2.17x. On one of the observed days, the temperature was 82 °F and 66 bags of ice were sold. Determine the number of bags of ice predicted to be sold by the LSR line, ŷ, when the temperature is 82 °F. Enter your answer as a whole number, rounding if necessary. ice bags Using the predicted value you just found, compute the residual at this temperature. residual = ice bags DOLL
Weight (pounds), x Miles per Gallon, y 3769 18 3937 15 2662 24 3612 18 3347 20 2917 24 3640 17 2668 24 3381 18 3880 17 3286 19
This is only one question
Is It Getting Harder to Win a Hot Dog Eating Contest?Every Fourth of July, Nathan’s Famous in New York City holds a hot dog eating contest. The table below shows the winning number of hot dogs and buns eaten every year from 2002 to 2015, and the data are also available in HotDogs. The figure below shows the scatterplot with the regression line. Year Hot Dogs 2015 62 2014 61 2013 69 2012 68 2011 62 2010 54 2009 68 2008 59 2007 66 2006 54 2005 49 2004 54 2003 45 2002 50 Winning number of hot dogs in the hot dog eating contest Winning number of hot dogs and buns Click here for the dataset associated with this question. (a) Is the trend in the data mostly positive or negative? Positive Negative (b) Using the figure provided, is the residual larger in 2007 or 2008?Choose the answer from the menu in accordance to item (b) of the question statement 20072008 Is the residual positive or…
Might we be able to predict life expectancies from birthrates? Below are bivariate data giving birthrate and life expectancy information for each of twelve countries. For each of the countries, both x, the number of births per one thousand people in the population, and y, the female life expectancy (in years), are given. Also shown are the scatter plot for the data and the least-squares regression line. The equation for this line is y = 82.17 -0.47x. Birthrate, x (number of births per 1000 people) 14.3 27.4 51.1 46.8 24.9 29.9 18.2 41.6 49.4 14.1 33.9 49.3 Send data to calculator Female life expectancy, y (in years) 75.6 70.5 58.2 59.0 73.3 62.7 73.6 65.2 62.4 74.3 67.0 53.9 Send data to Excel Female life expectancy (In years) Based on the sample data and the regression line, answer the following. 85+ 80+ 75+ 70+ 65 60 55+ 50 (a) From the regression equation, what is the predicted female life expectancy (in years) when the birthrate is 29.9 births per 1000 people? Round your answer to…

SEE MORE QUESTIONS

Recommended textbooks for you

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

Elementary Statistics: Picturing the World (7th E…

Statistics

ISBN:

9780134683416

Author:

Ron Larson, Betsy Farber

Publisher:

PEARSON

The Basic Practice of Statistics

Statistics

ISBN:

9781319042578

Author:

David S. Moore, William I. Notz, Michael A. Fligner

Publisher:

W. H. Freeman

Introduction to the Practice of Statistics

Statistics

ISBN:

9781319013387

Author:

David S. Moore, George P. McCabe, Bruce A. Craig

Publisher:

W. H. Freeman

SEE MORE TEXTBOOKS