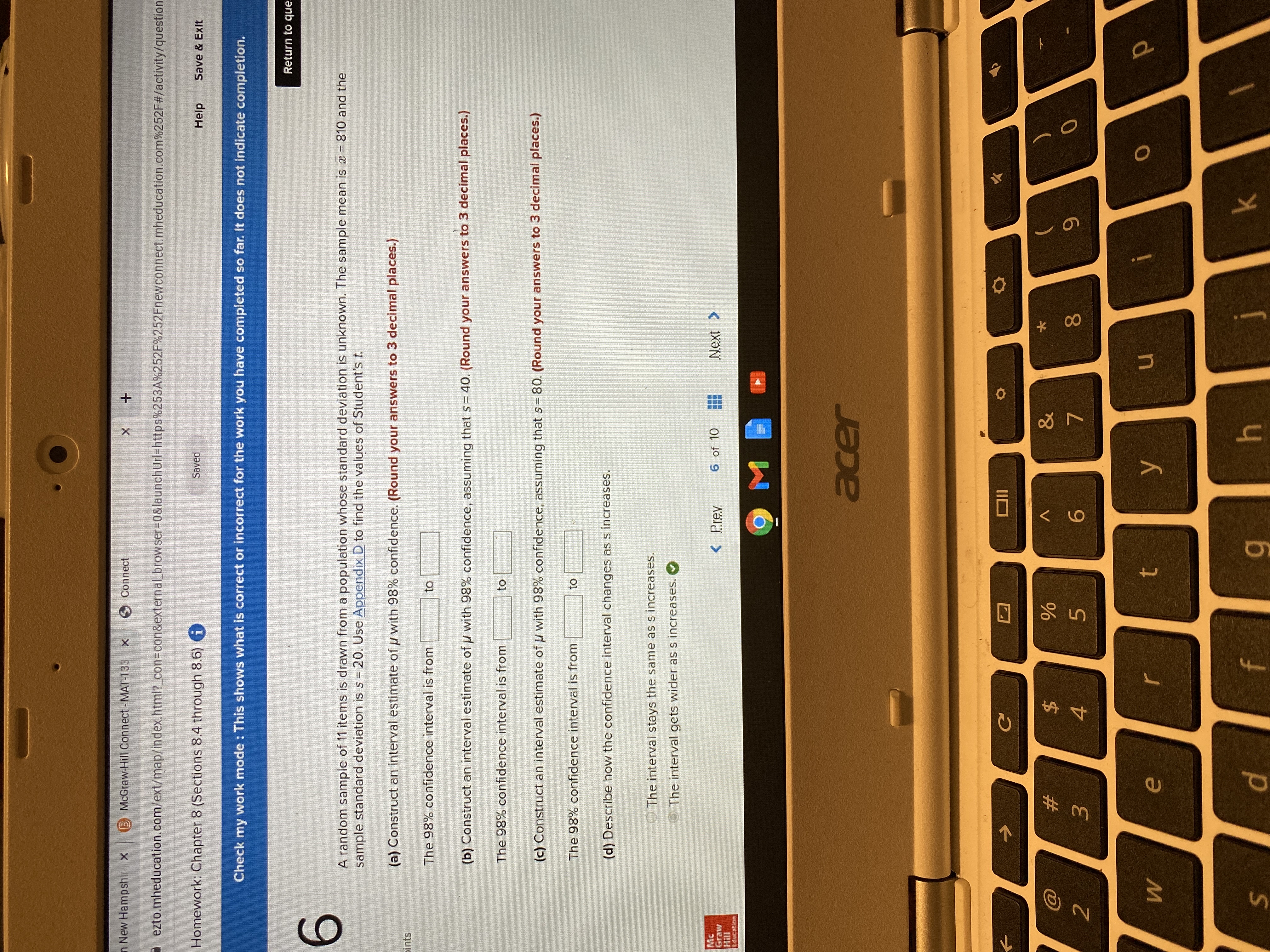
**Exercise: Confidence Interval Estimation** A random sample of 11 items is drawn from a population whose standard deviation is unknown. The sample mean is \( \bar{x} = 810 \) and the sample standard deviation is \( s = 20 \). Use Appendix D to find the values of Student’s t. **(a)** Construct an interval estimate of \( \mu \) with 98% confidence. *(Round your answers to 3 decimal places.)* The 98% confidence interval is from _______ to _______. **(b)** Construct an interval estimate of \( \mu \) with 98% confidence, assuming that \( s = 40 \). *(Round your answers to 3 decimal places.)* The 98% confidence interval is from _______ to _______. **(c)** Construct an interval estimate of \( \mu \) with 98% confidence, assuming that \( s = 80 \). *(Round your answers to 3 decimal places.)* The 98% confidence interval is from _______ to _______. **(d)** Describe how the confidence interval changes as \( s \) increases. - The interval stays the same as \( s \) increases. - The interval gets wider as \( s \) increases. (Correct) *Note: Please refer to the table in Appendix D for the appropriate t values for constructing these confidence intervals.*
Unitary Method
The word “unitary” comes from the word “unit”, which means a single and complete entity. In this method, we find the value of a unit product from the given number of products, and then we solve for the other number of products.
Speed, Time, and Distance
Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 miles away.
Profit and Loss
The amount earned or lost on the sale of one or more items is referred to as the profit or loss on that item.
Units and Measurements
Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experiments to set up the devices.
Help !!
From the given information,
Sample size n =11
sample mean, x̅=810
sample standard deviation, s=20
Confidence level = 98%
Degrees of freedom: 24(=25-1).
Using Excel function, “=T.INV.2T (0.02,10)”, the critical value for two-tailed test at 98% confidence level is 2.7638.
The standard error is:
Margin of error:
Confidence interval:
The 98% confidence interval is from 793.334 to 826.666.
Step by step
Solved in 4 steps
