"Show that the expected value of \(\hat{p}_N\) is \(p\)." Suppose you want to find out how many people support Policy \( X \). A standard polling approach is to just ask \( N \) many people whether or not they support Policy \( X \), and take the fraction of people who say yes as an estimate of the probability that any one person supports the policy. Suppose that the probability someone supports the policy is \( p \), which you do not know. Let \( \hat{p}_N \) be the number of people polled who supported the policy, divided by the total number of people polled \( N \).

Answered: Show that the expected value of îN is…

Math

Probability

Show that the expected value of îN is p.

A First Course in Probability (10th Edition)

10th Edition

ISBN:9780134753119

Author:Sheldon Ross

Publisher:Sheldon Ross

Chapter1: Combinatorial Analysis

Section: Chapter Questions

Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...

See similar textbooks

Related questions

Q: Let X, Y & Z be independent uniform random variables on the interval [ 0,1 ] . let W= min {X,Y,Z}…

A: Given information X,Y, Z ~U(0,1) W=min{X,Y,Z} X, Y and Z are independent.

Q: A construction consultancy firm calculates the probability that a dam project starts on time is P(S)…

A: Here we've to find P(F/S). We know that P(F/S)= P(F n S)/P(S) = P(S n F)/P(S) Given, P(S) = 0.83,…

Q: Consider a discrete random variable X with a pmf given by i) ii) iv) p(x) = cx2, if x = 1,2,3,4 0,…

Q: Let {X1, X2,..., Xn} be the scores from Midterm 1 and {Y₁, Y2, ..., Ym} be those from Midterm 2. We…

Q: Find the expected value of q. d. Let X1, X2,., Xn be i.i.d. Bernoulli(p). Suppose q =

A: Bernoulli Trail: In probability theory, a Bernoulli trial is a random experiment which has exactly…

Q: Let Z=3X-7Y, where X and Y are independent random variables. a) Determine the characteristic…

Q: Let X and Y be independent standard normal RVs. Suppose Z = X+2Y and W = X-Y a) Find the…

Q: Let X be a finite random variable with the expected value µ. Then the expectation E( (X – u)² ) of…

Q: COM C 2 1 ("skorjo, jossa avoy os submitus pencury (4) (XX 9 C C F inox puncs ['sophe the sonop and…

A: Let X = the number of people who arrive late for the seminar. Total no. of individuals (n) = 8…

Q: i) Show that the standard score of the sample mean X, is equal to Y. ii) Show that the mean and…

A: It is given that X follows N(θ, 1), then E(X) = θ and V(X) = 1, And the moment genarating function…

Q: E\VX{ + X}

A: Consider the provided question, Let X1,X2 be the two independent standard normal random variables.…

Q: Let X and Y be random variables with finite variance. Prove that |ρ(X, Y)| = 1 implies that there…

A: Let's assume that |ρ(X, Y)| = 1, which means that the correlation coefficient between X and Y is…

Q: Let X1, X2, X3,....., Xn be the independent identically distributed random variables and let Sm = X1…

A: Let X1, X2, X3,....., Xn be the independent identically distributed random variables let Sm = X1 +…

Q: equation (10.2.1) does not depend on 0 it f(x₁, x 0) if (x ((s: A)

A: Given: X1,X2,...Xn be the normal distribution such that S=∑i=1nxi2

Q: Assume that the coin is weighted so that Pr[H]=59, and that the coin is flipped until a head…

A: Given that the coin is flipped until a head appears, or 3 consecutive tails appear. The possible…

Q: Of those women who are diagnosed to have early-stage breast cancer, one-third eventually die of the…

A: As per the Given information For effective program

Q: For a uniform random variable U∼U(0,14)U∼U(0,14), find the probability P(U>11)P(U>11): P(U>11)

A: From the provided information, U~U(0, 14) a = 0 and b = 14

Q: Let pX(x) be the pmf of a random variable X. Find the cdf F(x) of X and sketch its graph along with…

Q: let X be a random variable and X is normally distributed

A: Given information: μ=35 and σ=4

Q: During the 2015–16 NBA season, Stephen Curry of the Golden State Warriors had a free throw shooting…

A: X~Bin(n=2, p=0.908)

Q: It is known that X is a random variable with PMF Px(x) = cx? for x = Px(x) = 0 otherwise. Each…

A: Solution

Q: given by f(k) = { pqk-1, k=1,2,... ... ... (0, elsewhere i) Derive the moment generating function of…

A: Given that b .And we have to find expected value of k c.. variance of k..

Q: Let Z be a random variabale satisfying N(0, 1). Without using the normalcdf(...) function, find P(Z…

A: The Z be the standard normal variate The mean is zero. The standard deviation is 1. Z~N(0,1)

Q: Let X1, X2, .. ,Xn form a random sample from B(1,0). Find minimal sufficient statistics.

Q: Let X1, X2, ….,n be iid random variables with common CDF F. Generate the random variable defined by…

A: This method uses the property that the minimum of n i.i.d. random variables with common CDF F…

Q: Assume that the length of a phone call in minutes is an exponential random variable X with parameter…

A: Solution: Let X be the length of a phone call. From the given information, X follows an exponential…

Q: Let X be a discrete random variable with moment generating function 1 M(t) 6. (e²t + e=) (e²r + e³r…

Q: Let denote H, - random event that demand for the new product is high, H, - that demand is average,…

Q: Let X1,..., X, be independent U (0, ve) random variables for some 0 <0< 1. Find an MLE of 0.

Q: When the error probability P[Accept HO | HO is false] is type l error. O True False

A: Given that, P(Accept H0 | H0 is false)

Q: Let X and Y be independent, identically distributed exponential random variables with parameter A,…

A: It is given that X and Y are independent and identically distributed exponential random variables…

Q: Suppose that a worker value jobs by both the wage rate and the workplace collegiality. The woker’s…

A: *Answer:

Q: Let X denote the number of empty bins when 60 balls are thrown independently into 30 bins. What is…

A: Let X denote the number of empty bins. Balls are thrown independently into bins. The number of balls…

Q: Let the random variable X denote the number of trials in ecess of r that are ed to achieve the r-th…

A: Given that, The random variable X as the number of trails in excess of r that are required to…

Q: A transmitter sends out a random number X which can take values of -1, 0, or 1, each with…

A: X can take the values of -1, 0, or 1, each with probability 13. So, the PMF of X is P(X=x)=13,…

Q: Let X be Poisson random variable with the mean λ. Find the value of λ that satisfies P(X = 0|X ≤ 2)…

A: Let X be a random variable which follows Poisson distribution with a population mean λ. X~P(λ) The…

Q: Let X; be independent Uniform(-6,6) random variables, for i=1, 2, ., 14. Let Y = X1+X2+...+X14 - (b)…

Q: P(-∞ < x≤ a₁₂) = P(a₁ ≤ x ≤ a₂) = P(a₂ ≤ x ≤ a3) = P(a3 ≤ x < ∞) = function p(x) a₁ = = 1 π(1 + x²)…

Q: Let X1, …, Xn be independent lognormal random variables and let a1, …, an be constants. Show that…

Question

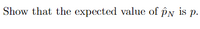
"Show that the expected value of \(\hat{p}_N\) is \(p\)."

Suppose you want to find out how many people support Policy \( X \). A standard polling approach is to just ask \( N \) many people whether or not they support Policy \( X \), and take the fraction of people who say yes as an estimate of the probability that any one person supports the policy. Suppose that the probability someone supports the policy is \( p \), which you do not know. Let \( \hat{p}_N \) be the number of people polled who supported the policy, divided by the total number of people polled \( N \).

Expert Solution

Step 1

Given that p denote the probability that someone aupports the policy.

And X denote the nunber of persons support Policy, out of N persons.

Step by step

Solved in 2 steps with 1 images

SEE SOLUTION Check out a sample Q&A here

Similar questions

A coin is tossed 4 times. Let X be the number of Heads on the first 3 tosses and Y be the number of Heads on the last three tossed. Find the joint probabilities pij = P ( X=i,Y=j) for all relevant i and j. Find the marginal probabilities pi+ and p+j for all relevant i and j.
be a random sample from N (H , oʻ) population. Find Xn Example 7: Let x1 , X2 , ... , sufficient estimators for µ and oʻ.
Let X and Y are independent Poisson random variables such that E(X) = E(Y)=2. Let Z=X+Y. Compute P(X=2|Z=3).
There are 3 boys and 2 girls at a party. Three party-goers are selected at random to go on a root-beer run. Let W denote the number of girls in the group of three that go on the root-beer run. Compute the expected number of girls who go on the root-beer run, E[W].
Consider a random variable X taking the values k1, k2, , km E R .. with probability ; Pn E [0, 1] 1. Write down the formula for the P1, P2, .. respectively, where p1 + P2 + expected value of f(X) for a given function f(-). + Pn ...
Show that the CDF of a geometric random variable with parameter p can be expressed as
Let X equal the IQ of a randomly selected American. Assume X ~ N( μ μ {"version":"1.1","math":"μ"} =100, σ σ {"version":"1.1","math":"σ"} =4). What is the probability that a randomly selected American has an IQ below 90?
a) Let X₁, X₂, X₁,...,X, be a random sample of size n from population X. Suppose that X-N(0, 1) and Y = -1-8√n. i) Show that the standard score of the sample mean X, is equal to Y. ii) Show that the mean and variance of the random variable Y are 0 and 1, respectively. iii) Show using the moment generating function technique that Y is a standard normal random variable. iv) What is the probability that Y2 is between 0.02 and 5.02?
Prove that the events Es, E2... En are independent iff their corresponding indicator variates I,, I₂.. In are independent.
Let Y1,..., Y, be i.i.d. random variables from the Weibull distribution f(y; 0) Σ (멤) exp ), y > 0. Show that ô = Li=1í is an unbiased estimator of 0. Is Ô an efficient estimaotr of 0?
prove
Compute the ff.: Expected Value of X ~ N(0, 1) Variance of X ~ N(0, 1) Moment Generating function of X ~ N(0, 1)